Расчёт показателей теоретического распределения
по дисциплине «Надёжность работы автомобильных дорог»
Студент Ламова А.Ю.
Руководитель проекта к.т.н., доцент И.В.Огнев
БАРНАУЛ 2012
Цель работы: освоить методы статистической обработки информации оботказах и определить основные характеристик надежности.
Немного теории (повторение пройденного)
Среднее арифметическое значение характеризует центр группирования случайных величин;
Дисперсия, среднее квадратическое отклонение и коэффициент вариации характеризуют степень разброса случайных величин около центра;
Асимметрия и эксцесс характеризуют соответственно степень не симметрии и тупости кривой распределения.
Законы распределения случайных величин отражают физическую сущность рассматриваемых явлений. Совокупность факторов или условий, приводящих к возникновению того или другого вероятностного закона, называют математической моделью явления. Применительно к нормальному закону математической моделью служат следующие условия:
- исследуемое явление является следствием или суммой воздействий достаточно большого количества различных случайных, независимых между собой или слабо зависимых источников;
- дисперсии и математические ожидания складываемых источников мало отличаются друг от друга, и от математического ожидания и дисперсии складываемой суммы.
При наличии указанных условий возникает нормальный закон, который находит широкое применение при решении различных инженерных и экономических задач.Применительно к математической теории надежности нормальный закон хорошо описывает постепенные отказы изделий, вызываемые выходом из строя их отдельных элементов.
Критерий согласия Пирсона применяется для проверки согласованности эмпирического и теоретического распределений.
Точечной называют опенку, которая определяется одним числом.
Интервальной называют оценку, которая определяется двумя числами - концами интервала.
Доверительным называют интервал, который покрывает неизвестный параметр с заданной надежностью 
.
Расчет
статистический аккумулятор надежность математический
Дано: имеется статистика отказов аккумуляторов. Было обследовано 20 аккумуляторов. Величина выработки аккумуляторов колеблется в пределах от 6100 км до 14700 км.
Определить параметры теоретического распределения и величину границ нижнего и верхнего интервала оценки математического ожидания выработки аккумляторов с доверительной вероятностью 0,95.
Решение: требуется решить следующие задачи:
- построить гистограмму опытных частот по пробегу и по ее виду решить в первом приближении вопрос о законе распределения (было в первой работе);
- для предполагаемого закона распределения построить теоретическую кривую частоты отказов по пробегу, найти основные параметры закона распределения, построить интегральную кривую;
- дать интервальную оценку математического ожидания.
Для удобства обработки весь объем выборки п обычно группируется в К разрядов (интервалов).
В нашем примере нижний пробег округлен до 6 тыс. км, верхний до 15 тыс. км. Их разность составила 6 тыс. км, что позволяет нам все измерения сгруппировать в 9 разрядов с величиной интервала в 6 тыс. км.
Определяем числовые характеристики статистического распределения.
Находим среднее арифметическое:
Определяем оценку дисперсии:
Находим оценку среднего квадратического отклонения:
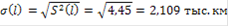
Определяем оценку величины коэффициента вариации:
Расчёт показателей теоретического распределения
За нулевую гипотезу принимаем, что теоретическое распределение является нормальным (исходя из вида гистограммы).
Нормальный закон распределения характеризуется плотностью вероятности:
где 
и 
- соответственно математическое ожидание и среднееквадратическое отклонение случайной величины
Определяем показатели теоретического распределения и строим графики. Определение точек теоретических кривых удобнее проводить в табличной форме, см. таблицу №1.
Таблица 1 - Расчёт теоритических кривых.
| № | Середина интервалов тыс. км. |  , тыс. км.
| z | 
| Теоретические частоты 
| Накопленная частость | |
| F(z) | в% | ||||||
| 6,5 | -4,19 | -1,99 | 0,06 | 0,53 | 0,02 | 2,35 | |
| 7,5 | -3,19 | -1,51 | 0,13 | 1,21 | 0,07 | 6,52 | |
| 8,5 | -2,19 | -1,04 | 0,23 | 2,21 | 0,15 | 14,96 | |
| 9,5 | -1,19 | -0,56 | 0,34 | 3,23 | 0,29 | 28,63 | |
| 10,5 | -0,19 | -0,09 | 0,40 | 3,77 | 0,46 | 46,41 | |
| 11,5 | 0,81 | 0,38 | 0,37 | 3,51 | 0,65 | 64,95 | |
| 12,5 | 1,81 | 0,86 | 0,28 | 2,62 | 0,80 | 80,46 | |
| 13,5 | 2,81 | 1,33 | 0,16 | 1,56 | 0,91 | 90,86 | |
| 14,5 | 3,81 | 1,81 | 0,08 | 0,74 | 0,96 | 96,46 | |
|
При этом теоретические частости подсчитываются через так называемую табличную плотность вероятности:
где 
Значения этой функции подсчитаны и приводятся в таблицах, содержащихся в литературе по математической статистике. Эта же таблица приведена в приложении 1 настоящего методического указания.
Теоретические частоты подсчитываются по формуле:
где 
- постоянный коэффициент.
Умножив цифры в пятой колонке на этот коэффициент мы получаем соответствующие им теоретические частоты, которые заносим в шестую колонку таблицы.
Для контроля правильности ваших действий необходимо на этом этапе в обязательном порядке подсчитать сумму теоретических частот. Она должна получиться чуть меньше объема выборки. В нашем примере она равна 19,36 что на 0,64 меньше 20. Это очень хороший результат указывает на правильность наших вычислений.
Если полученная сумма значительно меньше объема выборки или превышает ее, то дальнейшие расчеты надо приостановить и искать ошибку. Иногда она довольно проста и кроется в ошибке определения постоянного коэффициента с. Редкой, но более неприятной ошибкой является такая, причина появления которой заложена в самом начале расчетов. Она связана с грубыми просчетами в вычислениях среднего арифметического и среднего квадратического значений.
Рассчитываем интегральную функцию нормального распределения:
Для ее вычисления удобнее провести центрирование и нормирование данной функций, для чего положим:
Центрированная и нормированная, т.е. табличная функция нормального закона запишется так:
Для табличной интегральной функции составлена таблица, см. приложение 2. По величинеZ находим значения функции. Используя ее,занесем в гр. 7 таблицы №1 накопленные частости для каждого интервала, а в гр. 8 ее значение в процентах.
В отчете по лабораторно-практической работе выполняются два рисунка, на одном из которых изображается теоретическая кривая частот распределения отказов, а на другом - интегральная кривая частот отказов, см. рис. 1 и 2. При их выполнении необходимо соблюдать в установленном порядке существующие на данный момент стандарты.
Рисунок 1 - Гистограмма и теоритическая кривая
Рисунок 2 - Интегральная кривая