Из опубликованных работ были выбраны [77,83,85,91,93,97,98,99,100], удовлетворяющие следующим условиям: эксперименты проводились при атмосферном давлении с контролем температуры и фугитивности кислорода, приведены полные составы сосуществующих расплавов (стекол), шпинелей и оливинов. Был сформирован массив, состоящий из 92 точек многомерного пространства признаков. Каждая такая точка представляет собой как бы объединенный "анализ" - матрицу, состоящую из пересчитанных на атомные количества содержаний химических элементов в стеклах, шпинели и оливине, значений температуры и фугитивности.
Методика обработки данных. Включает пересчеты первичных составов стекол, шпинелей и оливина, полученных зондовым методом, и дальнейшую математическую обработку методом наименьших квадратов.
Составы стекол. В имеющихся составах стекол содержания FeO и Fe2O3 (если такое имелось, в виде весовых % окислов) пересчитывались в FeO (общее). Затем разделение на FeO и Fe2O3 проводилось по обобщенной формуле, предложенной в [10]. После этого рассчитывались атомные количества элементов: сначала с учетом содержания кислорода отношение K/O, где:
K = Si + Ti + Al + Cr + Fe3+ + Fe2+ + Mn + Ca + Na + K; O - кислород.
K/O варьировало от 41/59 до 38/62. Затем количество атомов кислорода вычиталось, а содержания элементов вновь пересчитывались на 100%.
Составы шпинелей и оливина. В имеющихся составах шпинелей содержания FeO и Fe2O3 также пересчитывались на FeO (общее), которое вновь разделялось на окисную и закисную формы по стехиометрии, и с учетом ульвошпинелевого компонента. Затем, составы шпинелей и оливина пересчитывались на атомные проценты, содержание кислорода вычиталось и остаток катионов нормировался до 100%.
При дальнейшей обработке мы исходили из отсутствия структурного мотива в расплавах, статистически беспорядочного распределения катионов в кристаллах шпинели между октаэдрическими и тетраэдрическими позициями, и из того, что распределение Fe и Mg по позициям M1 и M2 в оливине близко к случайному. Исследовалась связь между совместными значениями Fe2+/Mg в разных фазах, аппроксимированная по методу наименьших квадратов [70] линейной зависимостью. По получаемому уравнению вида y = A + B x; где: x - известное значение Fe2+/Mg в данной фазе; y - оцениваемое значение Fe2+/Mg в другой фазе; A и B - постоянные коэффициенты, вычислялось значение Fe2+/Mg в другой фазе. Сила связи оценивалась по величине коэффициента корреляции (R). По R оценивались также и влияние температуры (T), фугитивности кислорода (fO2) и активности элементов в расплаве. Стандартная ошибка ( ) определялась по уравнению:
) определялась по уравнению:
 (di) / (n-2) ], где di = yi (истинное) - yi (расчетное)
(di) / (n-2) ], где di = yi (истинное) - yi (расчетное)
Определялось также и значение абсолютной ошибки ( ). Распределение стандартной ошибки практически во всех случаях соответствовало гауссовскому, что позволило отбросить точки, для которых квадратичное отклонение было > 3
). Распределение стандартной ошибки практически во всех случаях соответствовало гауссовскому, что позволило отбросить точки, для которых квадратичное отклонение было > 3  . Их количество составляло ~ 4-7% от общего числа точек. Для оставшегося массива процедура расчетов вновь повторялась; эти результаты приведены в тексте. Все расчеты проводились с помощью программы "FASTVIEW" (автор - Ананьев В.В.).
. Их количество составляло ~ 4-7% от общего числа точек. Для оставшегося массива процедура расчетов вновь повторялась; эти результаты приведены в тексте. Все расчеты проводились с помощью программы "FASTVIEW" (автор - Ананьев В.В.).
Используемая форма представлений составов (атомные количества катионов) кажется более целесообразной в сравнении с традиционными. В таком виде данные точнее отражают как содержания элементов в каждой из фаз, так и отношения содержаний элементов между фазами, т.к. пропорциональны числу атомов, а не их весовой или молекулярной долям, что существенно для легких элементов типа Na и элементов с валентностями  2. Эта форма представления составов привычна для восприятия из-за небольших отличий цифровых значений от окисных весовых процентов, в отличие от атомных количеств с участием кислорода. Расчитываемое по валентностям количество кислорода является предельным для данной породы или расплава того же состава. В силикатных стеклах (расплавах) выделяются 3 разновидности кислорода: мостиковый (00), немостиковый (01-) и свободный (02-) [9]. Концентрации каждой из этих форм кислорода зависят от состава расплава, его структуры, состава флюида, температуры (T) и давления (P). Концентрация мостикового кислорода должна быть меньше предельной из-за существования наряду со связью
2. Эта форма представления составов привычна для восприятия из-за небольших отличий цифровых значений от окисных весовых процентов, в отличие от атомных количеств с участием кислорода. Расчитываемое по валентностям количество кислорода является предельным для данной породы или расплава того же состава. В силикатных стеклах (расплавах) выделяются 3 разновидности кислорода: мостиковый (00), немостиковый (01-) и свободный (02-) [9]. Концентрации каждой из этих форм кислорода зависят от состава расплава, его структуры, состава флюида, температуры (T) и давления (P). Концентрация мостикового кислорода должна быть меньше предельной из-за существования наряду со связью  Si-O-Si
Si-O-Si  связи
связи  Si-Si
Si-Si  "кислородная вакансия" [1] хотя не ясно, насколько велика их доля и как они зависят от вышеперечисленных параметров. Растворенная в расплаве Н2О (на примере альбитовой системы), по данным М.Б.Эпельбаума [76], влияет на соотношение мостиковой и немостиковой форм кислорода. По расчетам [43] такие флюидные компоненты, как Н2О и Н2, в процессе дегазации базальтовых расплавов увеличивают фугитивность кислорода, что должно, вероятно, сказываться и на концентрации различных форм кислорода в расплаве. F и Cl, постоянные участники магматического процесса, в расплавах образуют ионные группировки с катионами металлов [2,33], т.е. выполняют роль "свободного" кислорода. Эти наблюдения позволяют рассматривать рассчитываемое по валентностям содержание кислорода в предполагаемом расплаве как максимально возможное и без ущерба исключать из данных по составам. Кроме того, операция вычитания рассчитанного количества кислорода (практически постоянная величина: 59-62) и нормирование до 100% остатка с дальнейшим поиском корреляции между процентными величинами численно соответствует [62] нормированию на постоянную величину, кратную содержанию кислорода, и поиску истинного коэффициента корреляции между процентными величинами. В перспективе желательно научиться рассчитывать истинные концентрации трех форм кислорода в расплавах и знать, как связана фугитивность кислорода с концентрациями их в расплаве, и как влияет концентрация каждой из форм кислорода в расплаве и фугитивность кислорода в целом на его вязкость и т.д.
"кислородная вакансия" [1] хотя не ясно, насколько велика их доля и как они зависят от вышеперечисленных параметров. Растворенная в расплаве Н2О (на примере альбитовой системы), по данным М.Б.Эпельбаума [76], влияет на соотношение мостиковой и немостиковой форм кислорода. По расчетам [43] такие флюидные компоненты, как Н2О и Н2, в процессе дегазации базальтовых расплавов увеличивают фугитивность кислорода, что должно, вероятно, сказываться и на концентрации различных форм кислорода в расплаве. F и Cl, постоянные участники магматического процесса, в расплавах образуют ионные группировки с катионами металлов [2,33], т.е. выполняют роль "свободного" кислорода. Эти наблюдения позволяют рассматривать рассчитываемое по валентностям содержание кислорода в предполагаемом расплаве как максимально возможное и без ущерба исключать из данных по составам. Кроме того, операция вычитания рассчитанного количества кислорода (практически постоянная величина: 59-62) и нормирование до 100% остатка с дальнейшим поиском корреляции между процентными величинами численно соответствует [62] нормированию на постоянную величину, кратную содержанию кислорода, и поиску истинного коэффициента корреляции между процентными величинами. В перспективе желательно научиться рассчитывать истинные концентрации трех форм кислорода в расплавах и знать, как связана фугитивность кислорода с концентрациями их в расплаве, и как влияет концентрация каждой из форм кислорода в расплаве и фугитивность кислорода в целом на его вязкость и т.д.
Полученные результаты.

|
| Рис. 1 |
Для исследования поведения Fe2+/Mg в системе расплав (m) - шпинель (SP) - оливин (OL) был использован массив, сформированный из 92 точек. Выбраковано было 10 точек (по 5 для каждой из зависимостей: расплав - оливин и расплав - шпинель). Для дальнейших расчетов было использовано 82 точки, с диапазоном Fe2+/Mg отношений для расплава: 0,14-2,02. Были получены следующие результаты:
расплав-шпинель
[Fe2+/Mg]m = 0,64 [(Fe2+- Ti) / Mg ]sp + 0,13; R - 0,97;  - 0,078;
- 0,078;  - 0,104.
- 0,104.
Графически зависимость представлена на рис.1.
расплав-оливин
[Fe2+/Mg]m = 2,71 . [Fe2 / Mg]ol + 0,05; R - 0,98;  - 0,73;
- 0,73;  - 0,096.
- 0,096.
Графически зависимость представлена на рис.1.
Обычно для системы расплав-оливин распределение Fe2+/Mg представляют в таком виде:
КD = [Fe2+/Mg]ol / [Fe2/Mg]m KD среднее - 0,3508;  - 0,045;
- 0,045;  - 0,056;
- 0,056;

|
| Рис. 2 |
интервал значений КD: 0,26-0,5. KD [Fe2/Mg] имеет одно и то же численное значение для молекулярных и атомных количеств содержаний элементов.
Численные значения коэффициента КD пропорциональны содержаниям ряда элементов в расплаве: КD-Si (R-0,8); KD-Na (R-0,72); KD-K(R-0,64). Связь между температурой и КD имеет значение R=0,38. Невысокое (R-0,4) значение коэффициента корреляции имеет и связь отношения [Fe2+/Mg]sp/[Fe2+/Mg]m c температурой. Расчет [Fe2/Mg]m по оливину может быть представлен и в такой форме:
[Fe2+/Mg]m = {[Fe2+/Mg]ol / 0,35}. 0,95 + 0,05; R-0,98;  -0,073;
-0,073;  - 0,095.
- 0,095.
Графически зависимость представлена на рис. 2.
Оливин - шпинель в расплаве.
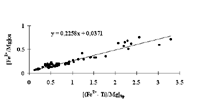
|
| Рис. 3 |
[Fe2+/Mg]ol = 0,23 [(Fe2+- Ti) / Mg]sp+ 0,04; R-0,96;  -0,036; d -0,048.
-0,036; d -0,048.
Графически зависимость представлена на рис.3
Шпинель - оливин в расплаве.
[(Fe2+-Ti) / Mg]sp= 4,06 . [Fe2+ /Mg]ol-0,08; R-0,96;  -0,147;
-0,147;  -0,199.
-0,199.
Графически зависимость представлена на рис. 4.

|
| Рис. 4 |
Зависимость [(Fe2+- Ti) / Mg]sp / [Fe2+/ Mg]ol (и наоборот) - Т (температура) имеет R-0,52 (интервал температур: 1100-1500oС). Полученные результаты, на достаточно большой по объему (82 точки) выборке, демонстрируют хорошую корреляцию (R-0,96) Fe2/Mg отношений в OL-SP (или SP-OL) ассоциациях, находящихся в равновесии с расплавом при атмосферном давлении.
Каждая из зависимостей (m-SP; m-OL) может быть представлена в более точном виде, полученными по более объемным выборкам с учетом Р и Т. Это дает уточненные зависимости в распределении Fe2+/Mg для ассоциации OL-SP (или SP-OL) сосуществующих с расплавом.
Расплав (m) - шпинель (SP). Используются два варианта уравнения: "равновесное" - 126 точек (1); "неравновесное" - 208 точек (2) [55]. Для разделения на "равновесные" и "неравновесные" составы фаз были использованы следующие характеристики условий опытов при атмосферном давлении: температура и продолжительность эксперимента [2].
[Fe2+/Mg]m = 0,75 [(Fe2+- Ti) / Mg]sp+ 0,04 R - 0,98;  -0,034;
-0,034;  - 0,044. (1)
- 0,044. (1)
[Fe2+/Mg]m = 0,65 [(Fe2+- Ti) / Mg]sp+ 0,1 R - 0,98;  -0,05;
-0,05;  - 0,065. (2)
- 0,065. (2)
Различия в коэффициентах уравнений (1) и (2) связаны с влиянием железистости расплава и "неравновесности" на вхождение Fe2+ и Ti в шпинель при ее кристаллизации [55]. В интервале значений 1 атм. - 1,5 ГПа влияние давления незаметно [55]. Для распределения [(Fe2+- Ti) / Mg]sp / [Fe2+/Mg]m ~ T o C в интервале 1100-1500o C R= 0,2, что свидетельствует о практическом отсутствии зависимости этого отношения от температуры [55].
Расплав-оливин. По результатам обработки имеющейся в нашем распоряжении выборки (82 точки, P=1 атм), можно утверждать следующее: [Fe2+/Mg]ol / [Fe2/Mg]m отношение (КD) лежит в интервале значений: 0,26-0,5; среднее: 0,35;  -0,045;
-0,045;  -0,056. Зависимость этого КD от температуры практически отсутствует (R-0,38). Вместе с тем существуют достаточно сильные корреляционные связи этого отношения с рядом элементов в расплаве: Si-КD (0,8); Na-КD (0,7); K- КD (0,6).
-0,056. Зависимость этого КD от температуры практически отсутствует (R-0,38). Вместе с тем существуют достаточно сильные корреляционные связи этого отношения с рядом элементов в расплаве: Si-КD (0,8); Na-КD (0,7); K- КD (0,6).
Относительно истинного значения КD и его зависимости от состава расплава, Т, Р пока единого мнения нет. В работах [78,89,96] приводятся значения КD: 0,3-0,33 + 0,03. Значения КD слабо зависят от температуры и давления. По данным [81,95], значения КD лежат в интервале 0,25-0,38, и зависят от концентрации SiO2 в расплаве и давления. Зависимость КD от давления (до значений Р ~ З ГПа) можно практически не учитывать [95]. По данным [101] в интервале давлений 105 ПА до 1,5 ГПа значение КD увеличивается на 0,03 относительно 0,3 (при 105 ПА), т.е. находится в пределах ошибки.
На основании приведенных выше данных можно утверждать, что в системе основной (ультраосновной) расплав - шпинель - оливин распределение Fe2+/Mg между этими фазами практически не зависит от температуры и давления до 1,5 ГПа. Зная закон распределения Fe2+/Mg отношения для OL-SP (SP-OL) ассоциации, находящейся в равновесии с расплавом, можно различать эту ассоциацию магматического генезиса от метаморфического.
Более точные значения коэффициентов в уравнениях, связывающих Fe2+/Mg в OL-SP (SP-OL) парах, кристаллизовавшихся из магматического расплава, можно получить, объединив приведенные выше результаты. Для оливина использованы два значения КD: 0,3 и 0,33, т.к. нормирование по SiO2 пока не проведено. Для шпинелей используются уравнения (1) и (2), "неравновесное" уравнение (2) целесообразно использовать для случая предполагаемых высокожелезистых расплавов с Fe2+/Mg > 1,4. В итоге, для каждого из случаев и OL-SP (расчет состава оливина по шпинели) и SP-OL (расчет состава шпинели по оливину) получено по 4 представленных ниже уравнения:
OL-SP
| [Fe2+/Mg]ol = 0,25.[(Fe2-Ti)/Mg]sp+ 0,01 [Fe2+/Mg]ol = 0,23.[(Fe2-Ti)/Mg]sp+ 0,01 | KD-0,3 "равновесные" (3) КD -0,33 (4) |
| [Fe2+/Mg]ol = 0,22.[(Fe2-Ti)/Mg]sp+ 0,03 [Fe2+/Mg]ol = 0,2.[(Fe2-Ti)/Mg]sp+ 0,03 | КD -0,3 "неравновесные" (5) КD -0,33 (6) |
 < 0,036; < 0,036;  < 0,048 < 0,048
|
SP-OL
| [(Fe2-Ti)/Mg]sp = 4. [Fe2+/Mg]ol -0,05 KD-0,3 "равновесные" (7) | [(Fe2-Ti)/Mg]sp = 4,4 . [Fe2+/Mg]ol -0,05 КD -0,33 (8) |
| [(Fe2-Ti)/Mg]sp = 4,6 . [Fe2+/Mg]ol -0,15 [(Fe2-Ti)/Mg]sp = 5,1. [Fe2+/Mg]ol -0,15 | КD -0,3 "неравновесные" (9) КD -0,33 (10) |
 < 0,147; < 0,147;  < 0,199 < 0,199
|
Обсуждение результатов.
Полученные в виде 8 уравнений цифровые зависимости позволяют рассчитывать Fe2+/Mg отношение в оливине по "равновесной" с составом данного кристалла шпинели, или, наоборот, по известному составу оливина - (Fe2-Ti)/Mg в шпинели. Расчеты по уравнениям для случаев КD =0,3 и КD =0,33 в каждой из 4 пар дают различия меньше стандартного отклонения. Уравнения (5,6,9,10) - условно "неравновесные" целесообразно использовать для случая образования OL-SP пар из высокожелезистых расплавов с Fe2+/Mg>1,4, а также для кристаллов основной массы эффузивов, эволюционировавших по феннеровскому пути. Ко всем уравнениям приводятся численные значения абсолютной ошибки ( ) и стандартного отклонения (
) и стандартного отклонения ( ), что позволяет с определенной долей вероятности (
), что позволяет с определенной долей вероятности ( - 70%, 2
- 70%, 2  - 95% [70]) судить о расплавном, или ином генезисе составов OL-SP пар в породе.
- 95% [70]) судить о расплавном, или ином генезисе составов OL-SP пар в породе.
Влияние давления до 1,5 ГПа, температуры (1100-1500oC) на распределение Fe2+/Mg отношения в системах расплав - шпинель и расплав - оливин не сказываются на численных значениях коэффициентов в уравнениях [55]. Соответственно и в уравнениях, связывающих оливин - шпинелевые пары, "равновесные" с основным-ультраосновным расплавом. T и P, в указанных интервалах, не влияют на распределение Fe2+/Mg отношения.
Все приведенные выше уравнения могут быть использованы для кристаллов шпинели, содержащих менее 6% вес. TiO2 и менее 50% вес. Al2O3 [55]. В высокоглиноземистые шпинели (Al2O3 более 50% вес.) магний из расплава входит более охотно по сравнению с высокохромистыми разностями. Это сказывается на числовых значениях уравнений распределения Fe2+/Mg. Для случая расплав - высокоглиноземистая шпинель к настоящему времени удалось получить только оценочные значения коэффициентов [55].
Разбалансировка Fe2+/Mg отношения в системе OL-SP (SP-OL) относительно равновесного с расплавом (т.е. не отвечающая одному или нескольким уравнениям) происходит на всех этапах становления магматической породы: охлаждение, нагрев, метаморфизм. Причем это рассогласование может быть зафиксировано численно путем учета величины, и отчетливо проявляется из-за различного характера поведения Fe2+ и Mg в оливине и шпинели при нагреве, остывании. Это было выявлено экспериментально [84] и подтверждено на природных объектах [87]. В работе [55] рассмотрены различные варианты этого явления и показано, что оно, вероятно, фиксируется и при метаморфических процессах.
Выявленные цифровые зависимости получены по экспериментальным данным, для которых понятия одновременность образования и равновесность составов OL-SP пар в расплаве однозначно связаны в подавляющем большинстве случаев, существование же отклонений может служить признаком некондиционности экспериментальных результатов [55]. Иначе на природных объектах. В горной породе одновременность или разновременность образования кристаллов шпинели и оливина может быть установлена по их структурным взаимоотношениям. Если же характер срастания установить не удается, то вопрос остается открытым. Равновесность же или неравновесность, с учетом зональности, мозаичности и т.д. в составах кристаллов может быть уверенно зафиксирована с помощью полученных уравнений. Эта оценка, соотнесенная со структурными особенностями породы, может быть очень полезной, и дать генетическую информацию.