Институт психолого-педагогического образования
Кафедра физико-математических дисциплин
ЗАДАНИЯ и методические указания к выполнению
Контрольных работ по дисциплине
«Прикладная Математика»
для студентов заочной формы обучения
направления подготовки 44.03.04 Профессиональное обучение (по отраслям)
профиля подготовки "Машиностроение и материалообработка",
профиля подготовки «Металлургия», профиля подготовки «Транспорт»
Екатеринбург
РГППУ
Задания и методические указания к выполнению контрольных работ по дисциплине « Прикладная математика », Екатеринбург, ФГАОУ ВО «Российский государственный профессионально-педагогический университет», 2016 - 30с.
| Автор: | канд. физ.-мат.наук, доцент | С.Д.Филиппов |
Одобрены на заседании кафедры физико-математических дисциплин. Протокол от 29.10.2015 г. №3.
| Заведующий кафедрой физико-математических дисциплин | С.В. Анахов |
Рекомендованы к печати научно-методической комиссией ИППО РГППУ.Протокол от 24.12.2015 №4.
| Председатель методической комиссии Института ППО | В.В. Пузырев | |
| Зам.директора НБ | Е.Н. Билева | |
| Директор Института ППО | И.И.Хасанова |
| © ФГАОУ ВО «Российский государственный профессионально-педагогический университет», 2016 ©С.Д.Филиппов, 2016 |
Цель контрольных работ – закрепление и проверка знаний, полученных студентами в процессе самостоятельного изучения учебного материала по данной дисциплине, а также выявление их умения применять полученные знания на практике.
Указания к выполнению контрольных работ
При выполнении контрольных работ необходимо руководствоваться следующими требованиями:
1. Вариант контрольной работы выбирать по последней цифре номера зачетной книжки.
2. Каждую контрольную работу следует выполнять в отдельной тетради.
3. На обложке тетради должны быть ясно написаны название дисциплины, номер контрольной работы, фамилия студента, его инициалы, номер группы и шифр специализации, шифр зачетной книжки.
4. В начале работы должен быть указан номер варианта задания.
5. Перед решением задачи должно быть полностью приведено ее условие.
6. Решение задач следует сопровождать необходимыми формулами, развернутыми расчетами и краткими пояснениями.
7. В конце работы должна стоять подпись студента с указанием даты ее выполнения.
Задача 1.
1.1. Дана функция  .
.
Показать, что  .
.
1.2. Дана функция  .
.
Показать, что  .
.
1.3. Дана функция  .
.
Показать, что  .
.
1.4. Дана функция 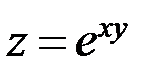 .
.
Показать, что 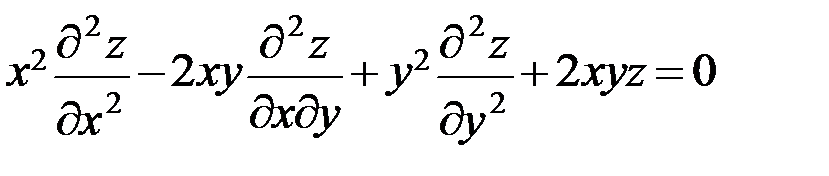 .
.
1.5. Дана функция  .
.
Показать, что  .
.
1.6. Дана функция  . Показать, что
. Показать, что  .
.
1.7. Дана функция  .
.
Показать, что  .
.
1.8. Дана функция  .
.
оказать, что  .
.
1.9. Дана функция  .
.
Показать, что  .
.
1.10. Дана функция  .
.
Показать, что  .
.
Задача 2.
Найти наименьшее и наибольшее значения функции z=f(x, y) в ограниченной замкнутой области D, заданной системой неравенств. Сделать чертеж.
2.1. 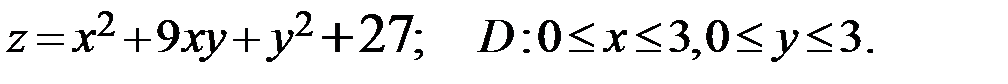
2.2. 
2.3. 
2.4. 
2.5. 
2.6. 
2.7. 
2.8. 
2.9. 
2.10. 
Задача 3.
Дана функция z=z(x, y), точка А(х0, у0) и вектор  . Найти: 1)
. Найти: 1)  в точке A; 2) производную в точке A по направлению вектора
в точке A; 2) производную в точке A по направлению вектора  .
.
3.1.  .
.
3.2.  .
.
3.3.  .
.
3.4.  .
.
3.5.  .
.
3.6.  .
.
3.7.  .
.
3.8.  .
.
3.9.  .
.
370.  .
.
Задача 4.
Найти неопределенные интегралы. В двух примерах (пункты а) и б)) проверить результаты дифференцированием.
4.1. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 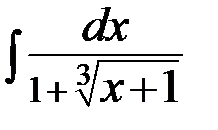 .
.
4.2. а) 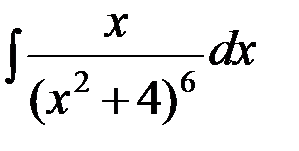 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4.3. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4.4. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4.5. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4.6. а) 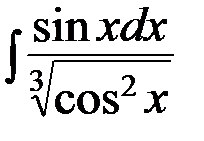 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4.7. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4.8. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4.9. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4.10. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 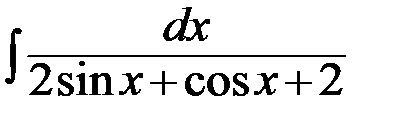 .
.
Задача 5.
Вычислить несобственный интеграл или доказать его расходимость.
5. 1.  . 5. 2.
. 5. 2.  .
.
5. 3.  . 5. 4.
. 5. 4.  .
.
5. 5.  . 5.6.
. 5.6.  .
.
5. 7. 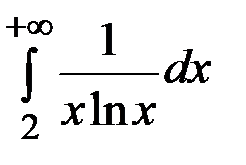 . 5. 8.
. 5. 8.  .
.
5. 9.  . 5.10.
. 5.10.  .
.
Задача 6.
Найти общее решение дифференциального уравнения.
6.1.  . 6.2.
. 6.2.  .
.
6.3..  . 6.4.
. 6.4.  .
.
6.5.  . 6.6.
. 6.6.  .
.
6.7.  . 6.8.
. 6.8.  .
.
6.9.  . 6.10.
. 6.10.  .
.
Задача7.
Найти частное решение дифференциального уравнения 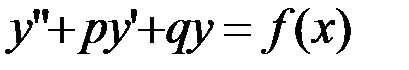 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  ,
,  .
.
7.1.  ;
;  ,
,  .
.
7.2.  ;
;  ,
,  .
.
7.3.  ;
;  ,
,  .
.
7.4.  ;
;  ,
,  .
.
7.5.  ;
; 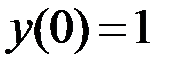 ,
,  .
.
7.6.  ;
;  ,
,  .
.
7.7.  ;
;  ,
,  .
.
7.8.  ;
;  ,
,  .
.
7.9.  ;
;  ,
,  .
.
7.10. 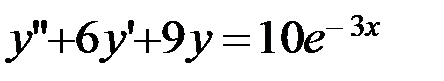 ;
;  ,
,  .
.
Задача 8.
Вычислить двойные интегралы по области D.
8.1. 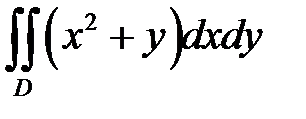 , где D – область, ограниченная линиям
, где D – область, ограниченная линиям 
8.2.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
8.3.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
8.4.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
8.5.  где D – область, ограниченная линиями
где D – область, ограниченная линиями 
8.6.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
8.7.  где D – область, ограниченная линиями
где D – область, ограниченная линиями 
8.8.  где D – область, ограниченная линиями
где D – область, ограниченная линиями 
8.9.  , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
8.10.  где D – область, ограниченная линиями
где D – область, ограниченная линиями
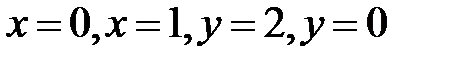 .
.
Задача 9.
Перейдя к полярным координатам (если требуется), вычислить площадь фигуры, ограниченной областью D.
9.1. Область D ограниченна линиями:  (І ая четверть)
(І ая четверть)
9.2. Область D ограниченна линиями:  .(І ая четверть)
.(І ая четверть)
9.3. Область D ограниченна линиями:  . (І ая четверть)
. (І ая четверть)
9.4. Область D ограниченна линиями: 
9.5. Область D ограниченна лемнискатой:  (І ая четверть)
(І ая четверть)
9.6. Область D ограниченна линиями: 
9.7. Область D ограниченна линиями: 
9.8. Область D ограниченна линиями: 
9.9. Область D ограниченна линиями: 
9.10. Область D ограниченна лемнискатой: 
Задача 10.
Вычислить криволинейные интегралы 2-го рода
10.1.  где L – контур треугольника, образованного осями координат и прямой
где L – контур треугольника, образованного осями координат и прямой  в положительном направлении, т.е. против движения часовой стрелки.
в положительном направлении, т.е. против движения часовой стрелки.
10.2.  где L– дуга параболы
где L– дуга параболы  от точки О (0;0) до точки
от точки О (0;0) до точки
А(2;4).
10.3.  где L – контур прямоугольника, образованного прямыми
где L – контур прямоугольника, образованного прямыми
 в положительном направлении (против часовой стрелки).
в положительном направлении (против часовой стрелки).
10.4.  вдоль кривой
вдоль кривой  .
.
10.5.  вдоль кривой
вдоль кривой  от точки О (0;0) до точки А(1;1).
от точки О (0;0) до точки А(1;1).
10.6. 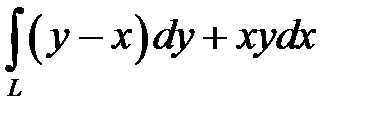 вдоль
вдоль  отточки О (0;0) до точки А(1;1).
отточки О (0;0) до точки А(1;1).
10.7. 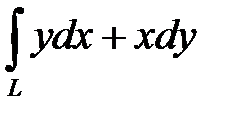 , где L– четверть окружности
, где L– четверть окружности  0
0  , против часовой стрелки.
, против часовой стрелки.
10.8.  , где L– первая арка циклоиды
, где L– первая арка циклоиды  0
0  .
.
10.9.  вдоль линии
вдоль линии  от точки О (0;0) до точки А(1;1).
от точки О (0;0) до точки А(1;1).
10.10. 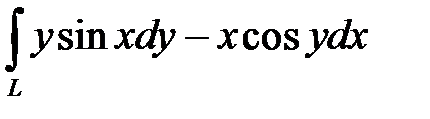 вдоль отрезка ОА, О (0;0),
вдоль отрезка ОА, О (0;0),  .
.
Задача 11.
Исследовать сходимость числового ряда.
12.1.  . 12.2.
. 12.2.  .
.
41..  . 12.4.
. 12.4.  .
.
12... 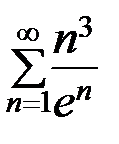 . 12...
. 12...  .
.
12.7.  . 12.8.
. 12.8.  .
.
12.9.  . 12.10.
. 12.10.  .
.
Задача 13.
Найти интервал сходимости степенного ряда.
13.1.  . 13.2.
. 13.2.  .
.
13.3.  . 13.4.
. 13.4.  .
.
13.5.  . 13.6.
. 13.6.  .
.
13.7.  . 13.8.
. 13.8.  .
.
13.9.  . 1310.
. 1310. 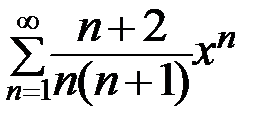 .
.
Задача 14.
Вычислить определенный интеграл  с точностью до 0,001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно.
с точностью до 0,001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно.
14.1.  . 14.2.
. 14.2.  .
.
14.3. 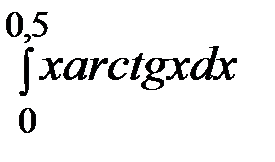 . 14.4.
. 14.4.  .
.
14.5.  . 14.6.
. 14.6. 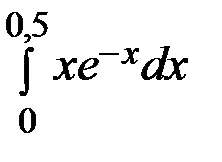 .
.
14.7.  . 14.8.
. 14.8.  .
.
14.9.  . 14.10.
. 14.10.  .
.
Методические указания и образцы решения задач.
Задача 1.
Показать, что функция  удовлетворяет равенству:
удовлетворяет равенству:

Решение. Находим частные производные функции по  и по
и по  :
:
 Подставим в равенство частные производные.
Подставим в равенство частные производные.

 ;
;

что и требовалось показать.
Задача 2
Найти наименьшее и наибольшее значения функции 
в области


Решение.
а) Найдём стационарные точки

Точка М  - стационарная, но не принадлежит области D.
- стационарная, но не принадлежит области D.
б) Исследуем данную функцию на границах квадрата АВСD.
Отрезок АВ: 

Функция  принимает наибольшее
принимает наибольшее  и наименьшее
и наименьшее  значения на концах отрезка
значения на концах отрезка  :
:

Отрезок BC: 


Отрезок CD: 


Отрезок DA: 
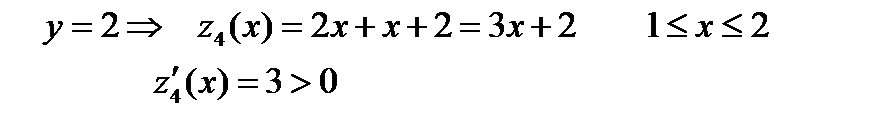

Найденные значения z сравним и получим

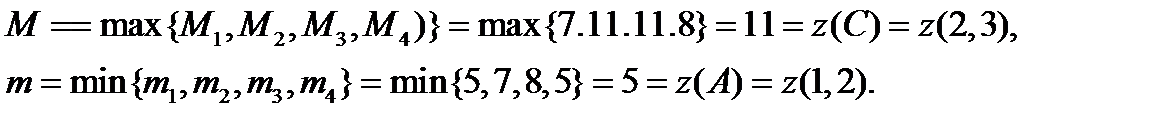
Наибольшее значение М равно 11 и достигается при х=2 и у=3, наименьшее значение m равно 5 и достигается при х=1 и у=2/
Задание3.
Дана функция  точка
точка  и вектор
и вектор 
 Найти
Найти  в точке
в точке  и производную в точке
и производную в точке  по направлению вектора
по направлению вектора  .
.

Найдём частные производные и вычислим их значение в точке  .
. 


 – направляющие косинусы вектора
– направляющие косинусы вектора 

Литература к заданиям 1.1 – 240, 2.1 – 2.0,2.1 – 270 – [4, гл. VIII, §§1-2, §4].
Задача 4.
Найти неопределённые интегралы, выполнив проверку дифференцированием в первых двух примерах.

Решение:

Проверка:


Используем метод интегрирования по частям для функции 
Формула:  Имеем
Имеем

Проверка:


Найдём коэффициенты








Задача 5
Вычислить несобственный интеграл

Несобственный интеграл расходится.
Методы интегрирования рассматриваются в учебном пособии [4, ч. I, гл. IХ. §§1-4].
Задача 6.
В данном задании предлагается решить дифференциальное уравнение одного из трёх типов – однородное, линейное или с разделяющимися переменными. Предлагается решение однородного уравнения.
Найти общее решение дифференциального уравнения первого порядка.

 .
.
Уравнение является однородным.
Функции 
 однородные второго порядка.
однородные второго порядка.
Уравнение можно привести к виду
 , разделив обе части его на
, разделив обе части его на  а затем на
а затем на  .
.

Введём подстановку

Разделяем переменные:

Интегрируем обе частиравенства,получаем

Кроме того,  также является решением.
также является решением.
Множество решений примет вид

Задача 7.
Найти общее и частное решения дифференциального уравнения
 при начальных условиях
при начальных условиях  .
.
Решение. Ищем общее решение в виде 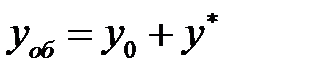 , где
, где  - общее решение однородного уравнения,
- общее решение однородного уравнения,  - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
Решаем однородное уравнение.
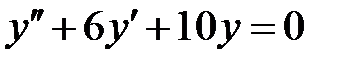 имеет характеристическое уравнение
имеет характеристическое уравнение 
корни которого равны  .Тогда
.Тогда
 -
-
является общим решением однородного уравнения
Находим частное решение данного уравнения.
Учитывая стандартную формулу правой части  , находим
, находим  -коэффициент при х в показателе степени. Число
-коэффициент при х в показателе степени. Число  не является корнем характеристического уравнения
не является корнем характеристического уравнения  поэтому
поэтому  подбираем в виде
подбираем в виде 
Найдём  Для этого подставим
Для этого подставим  в исходное дифференциальное уравнение
в исходное дифференциальное уравнение


Общее решение данного уравнения

Для поиска частного решения, удовлетворяющего начальным условиям, сначала найдем 

В равенства (1) и (2) подставим начальные условия: 
 , и окончательно получаем
, и окончательно получаем

Тема «Обыкновенные дифференциальные уравнения» рассмотрена в пособии [4, ч. II, гл. IV].
Задача 9.
Вычислить  где D – область, ограниченная линиями
где D – область, ограниченная линиями 

Решение. Область Dявляется правильной в направлении оси Оу, поэтому вычисление двойного интеграла сводится к вычислению повторного интеграла по формуле


Задача 9.
Вычислить двойной интеграл  если область D ограничена окружностями
если область D ограничена окружностями 

Решение. Для вычисления интеграла перейдем к полярным координатам, используя формулы перехода
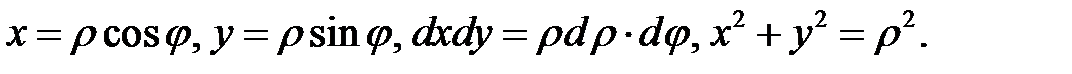
При этом исходная область интегрирования в полярных координатах переходит в прямоугольник 

Внутренний интеграл вычисляем методом интегрирования по частям

В результате 
**Типовые задачи по теме «Кратные интегралы» рассматриваются в учебном пособии [4, ч.  , гл.
, гл.  ,§§1-6].
,§§1-6].
Задача10.
Вычислить криволинейный интеграл

по дуге  кривой, заданной параметрически
кривой, заданной параметрически

Найдем dx и dy

Тогда 




Задача11.
Исследовать сходимость числового ряда

Решение. Для исследования данного ряда применяем признак Даламбера:
 , ряд расходящийся,
, ряд расходящийся,  сходящийся,
сходящийся,  нет ответа по данному признаку.
нет ответа по данному признаку.
 по данному условию, составим
по данному условию, составим

Значит данный ряд сходящийся.
Задача 13.
Найти область сходимости степенного ряда

Решение.Прежде всего определяется радиус сходимости степенного ряда


Значит интервал сходимости 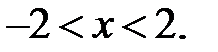
На границах интервала рассматриваются числовые ряды.
При 
Так как предел  то ряд расходится.
то ряд расходится.
При 
 –знакочередующийся ряд.
–знакочередующийся ряд.
Так как предел  не существует то ряд расходится.
не существует то ряд расходится.
Таким образом область сходимости ряда – интервал (-2;2).
Задача 14.
Вычислить определённый интеграл  с точностью 0,001,.
с точностью 0,001,.
Решение. Разложим подынтегральную функцию в ряд, а затем проинтегрируем её почленно.


 .
.
Используя разложение в ряд Маклорена функции
 , запишем разложение
, запишем разложение

Проинтегрировав, получим:

Значение интеграла равно сумме знакочередующегося ряда, а по теореме Лейбницаего сумма отличается от конечного отрезка ряд не более чем на первый отброшенный член.Шестойчлен ряда равен  поэтому в качестве приближенного значения интеграла берем первые пять слагаемых.Отсюда
поэтому в качестве приближенного значения интеграла берем первые пять слагаемых.Отсюда

с точностью 0,001.
Типовые задачи по теме «Ряды» рассматриваются в учебном пособии [4, ч.  , гл.
, гл.  ,§§1-6].
,§§1-6].
Литература
Основная литература
1. Шипачев В. С. Высшая математика. Базовый курс: учебник и практикум для бакалавров [Гриф Минобразования РФ] / В. С. Шипачев; под ред. А. Н. Тихонова. - 8-е изд., перераб. и доп. - Москва:Юрайт, 2015. - 447 с.
2. Шипачев В. С. Высшая математика. Полный курс: учебник для акад. бакалавриата [Гриф УМО] / В. С. Шипачев; под ред. А. Н. Тихонова. - 4-е изд., испр. и доп. - Москва:Юрайт, 2015. - 608 с
5. Ляховский В. А. Курс математики для технических высших учебных заведений: учебное пособие для вузов [Гриф УМО]. Ч. 2: Функции нескольких переменных. Интегральное исчисление. Теория поля / В. А. Ляховский, А. И. Мартыненко, В. Б. Миносцев; под ред. В. Б. Миносцева, Е. А. Пушкаря. - 2-е изд., испр. - Санкт-Петербург; Москва; Краснодар: Лань, 2013. - 428 с.
4. Данко П.Е., Попов А.Г., Кожевникова Т..Я. Высшая математика в упражнениях и задачах [Текст] / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. В 2 ч. – М.: Высшая школа, 2007. – 304+415с.
Дополнительная литература:
1. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. [Текст] / Б.П. Демидович, В.А. Кудрявцев. – М.: ООО "Изд. Астрель", 2001.- 437с.
2. Курс математики для технических высших учебных заведений [Электронный ресурс]: учебное пособие для вузов [Гриф УМО]. Ч. 4: Теория вероятностей и математическая статистика / Н. А. Берков [и др.]; под ред. Е. А. Пушкаря, В. Б. Миносцева. - 2-е изд., испр. - Электрон. текстовые дан. - Санкт-Петербург; Москва; Краснодар: Лань, 2013. - 304 с.
3. Курс математики для технических высших учебных заведений [Электронный ресурс]: учебное пособие для вузов [Гриф Минобразования РФ]. Ч. 3: Дифференциальные уравнения. Уравнения математической физики. Теория оптимизации / Н. А. Берков [и др.]; под ред. В. Б. Миносцева, Е. А. Пушкаря. - 2-е изд., испр. - Электрон. текстовые дан. - Санкт-Петербург; Москва; Краснодар: Лань, 2013. - 513 с.
4. Курс математики для технических высших учебных заведений: учебное пособие для вузов [Гриф Минобразования РФ]. Ч. 1: Аналитическая геометрия. Пределы и ряды. Функции и производные. Линейная и векторная алгебра / В. Г. Зубков и др.; под ред. В. Б. Миносцева, Е. А. Пушкаря. - 2-е изд., испр. - Санкт-Петербург; Москва; Краснодар: Лань, 2013. - 542 с.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления [Текст] / Н.С. Пискунов. В 2-х т. – М.: Интеграл-Пресс, 2005.- 460+560с.
ЗАДАНИЯи методические указания к выполнению