А теперь давайте вернёмся в наше физическое пространство и рассмотрим более скромный конкретный пример – обычный математический маятник. Давайте попробуем использовать метод построения динамики в обобщённых координатах – метод Лагранжа для нахождения закона его движения.
У математического маятника, колеблющегося в заданной плоскости – всего одна обобщённая координата – угол отклонения от вертикали 
Нам требуется найти вид его функции Лагранжа (5.6)
и вставить её (в конкретном виде) в уравнение Лагранжа
(5.7)
Причём, если пренебречь трением, внешних непотенциальных сил в данном случае нет:
(5.7в)
Если нам удастся это сделать, мы получим дифференциальное уравнение относительно обобщённой координаты (она в данном случае одна) и её производных по времени. Для нахождения уравнения движения, то есть функции координаты от времени 
останется решить дифференциальное уравнение.
Для начала требуется выразить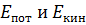 
как функции обобщённой координаты и её производных по времени.
Выражение для потенциальной энергии в однородном поле тяготения 
в данном случае, как видно из рисунка, обретает вид:
(5.12)
Потенциальную энергию можно отсчитывать от любого условного нулевого уровня. На конечном результате это не скажется, ведь путь к нему будет лежать через дифференцирование. Поэтому потенциальную энергию маятника мы можем выразить так:
(5.12а)
Теперь выразим кинетическую энергию. Нам в этом опять поможет рисунок.
(5.13)
Подставив выражения потенциальной и кинетической энергий из формул (5.12а) и (5.13) в общую формулу функции Лагранжа (5.6), получим конкретный вид функции Лагранжа для математического маятника:
(5.14)
Вставляем эту функцию Лагранжа (5.14) в уравнение Лагранжа (5.7в):
(5.15)
Выглядит громоздко. Но здесь, как видим, мы имеем тот упрощающий решение случай, когда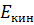 
явно зависит только от обобщённой скорости 
, но не обобщённой координаты , а 
наоборот, зависит только от координаты , но не скорости . Поэтому производная потенциальной энергии по скорости и производная кинетической энергии по координате равы нулю и их можно исключить из формулы:
(5.15а)
Теперь сократим эту формулу на 
. В результате масса 
полностью исключается из неё. Значит, закон движения математического маятника не зависит от его массы:
(5.15б)
Подставляем производные (производная от «косинуса» – «минус синус», производная от «фи с точкой в квадрате» – «два фи с точкой»):
(5.15в)
Сокращаем двойки и вместо 
пишем 
(это одно и то же, каждая точка над символом означает дифференцирование по времени):
(5.15г)
Это – конкретный вид уравнения Лагранжа для данного случая.
В учебных задачах часто спрашивают вид уравнения Лагранжа, а то и просто вид функции Лагранжа для той или иной (механической) системы. Мы же спросим себя, в чём смысл этого уравнения Лагранжа? В том, что это не что иное, как дифференциальное уравнение, описывающее движение математического маятника.
Правда, уравнение это хотя выглядит просто, но решается непросто (то есть, непросто из него получить из него функцию . Это нелинейное дифференциальное уравнение (в том смысле, что зависимость между и нелинейная, не прямо пропорциональная) Оно описывает нелинейные колебания – не синусоидальные, такие, при которых частота зависит от амплитуды. Лишь в случае малых амплитуд колебания «стремятся к линейным» в той мере, в которой значение 
стремится к значению самого угла , выраженному в радианах. И в этом случае закон движения маятника , как известно из курса средней школы, стремится к выражению:
(5.16)
где коэффициент при 
, а именно выражение 
– это частота его колебаний.
Теория колебаний – это очень интересная тема, ст о ящая отдельной беседы. Сегодня хочется сказать, что в познании природы бывает важно найти сам закон в виде дифференциального уравнения (в нашем случае ). Решение дифференциального уравнения может представлять большие технические трудности (вспомним, кстати, задачу трёх тел из третьей беседы, которая вообще не имеет аналитического решения). Но это уже, с позволения сказать, скорее технические, а не гносеологическиетрудности…