Тема: Перпендикуляр и наклонная. Расстояние от точки до плоскости
Дата: 05.10.2021 г.
Группа: П-263
Цели урока:закрепление понятий: перпендикуляр к плоскости, наклонная, основание наклонной, основание перпендикуляра, проекции наклонной на плоскость, расстояния от точки до плоскости
Студенты должны знать: определение перпендикулярности прямой и плоскости, перпендикуляра и наклонной, основание наклонной, основание перпендикуляра, проекции наклонной на плоскость, расстояния от точки до плоскости
Студенты должны уметь: применять признак при решении задач, графически изображать перпендикулярные прямые к плоскости, перпендикуляра и наклонной
Актуализация знаний студентов
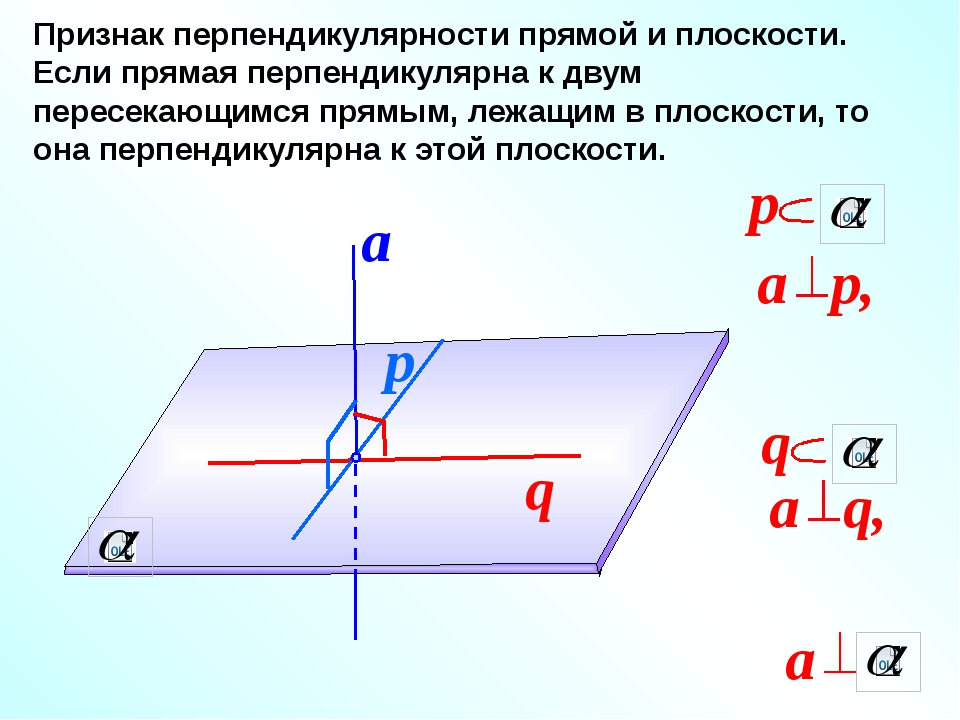
Актуализация опорных знаний.
Вопросы:
1. Угол между прямыми равен 90º. Как называются такие прямые?
/перпендикулярные/
2. Верно ли утверждение: «Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости»?
/ да /
3. Сформулируйте признак перпендикулярности прямой и плоскости.
/Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости./
4. Как определяется расстояние от точки до прямой на плоскости? От точки до плоскости?
/Как длина перпендикуляра, поведенного из точки к данной прямой./
2.Решение задач
Задача № 1
Задача № 2
Через вершину В ромба АВСD проведена прямая ВМ перпендикулярно к его плоскости. Найти расстояние от точки М до прямых, содержащих стороны ромба, если АВ = 25 см; ∠ВАD = 60º; ВМ = 12,5 см.
Решение:
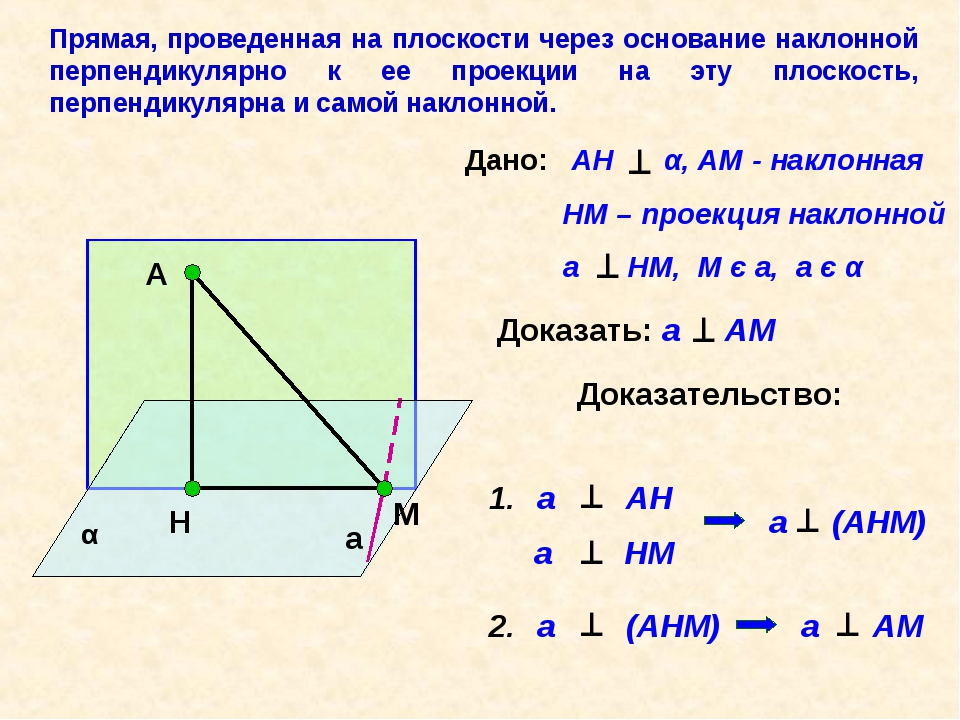
Проведем ВК ⊥ AD. ВК – проекция наклонной МК на плоскость ромба; AD ⊥ ВК, то AD ⊥ МК (по теореме о трех перпендикулярах). Длина МК – расстояние от точки М до прямой AD. МЕ – расстояние от точки М до прямой DC.
|
|
Из треугольника АВК: ВК = АВsin60º =.
МВК – прямоугольный (= 90º), так как МВ ⊥ (АВС); МК = = 25 (см).
ВК = ВЕ (как высоты ромба); (по двум катетам, как прямоугольные); МЕ = МК = 25 (см).
Расстояние от точки М до прямых АВ и ВС равны длине перпендикуляра МВ, то есть 12,5 см.
Ответ: 25 см; 25 см; 12,5 см; 12,5 см.
Задача № 3
Луч ВА не лежит в плоскости неразвернутого угла CBD. Докажите, что если, причем, то проекцией луча ВА на плоскость CBD является биссектриса ∠CBD.
1) Пусть АЕ ⊥ (CBD). В плоскости (АВС) проведем перпендикуляр АМ к прямой ВС, а в плоскости (АВD) перпендикуляр АК к прямой BD.
Так как,то точка М лежит на луче ВС (а не на продолжении этого луча). Аналогично, так как ∠ABD < 90°, то точка К лежит на луче BD. Так как ВС ⊥ АМ, то ВС ⊥ ЕМ (по теореме, обратной теореме о трех перпендикулярах).
Аналогично доказывается, что BD ⊥ ЕК.
2) = по гипотенузе (АВ – общая сторона) и острому углу (∠АВС = ∠ABD), то ВМ = ВК;
3) по гипотенузе (ВЕ – общая сторона) и катету (ВМ = ВК), то ЕМ = ЕК;
4) Точка Е равноудалена от сторон ∠СВD, значит, она лежит на биссектрисе этого угла, то есть луч ВЕ – биссектриса.
3.Домашнее задание:
Критерии оценивания:
1.Оценка «отлично» - выставляется обучающемуся, если правильно решены все задания, выполнены в полной мере, изложены логично.
1. Оценка «хорошо» - выставляется обучающемуся, если допущены незначительные погрешности в задании.
2. Оценка «удовлетворительно» - выставляется обучающемуся, если ответ на вопрос нелогичный, не полный.
|
|
3. Оценка «неудовлетворительно» - выставляется обучающемуся, если задания не решены.
ВНИМАНИЕ!!!
Уважаемые студенты, практическое задание необходимо выполнить в рабочей тетради (сфотографировать) или в формате Документа Word. Отправлять для проверки в личные сообщения на страницу ВКонтакте:https://vk.com/kolomiyetssg?z=photo95751036_324720501%2Falbum95751036_0%2Frev
Преподаватель: Коломиец Светлана Григорьевна