Задание номер 1.
1. В городе N живет 200000 жителей. Среди них 15 % детей и подростков. Среди взрослых 35% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?
Ответ:________
2. Клиент взял в банке кредит 3000 рублей на год под 16 %. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
Ответ:________
3. Поезд Москва-Волгоград отправляется в 13:40, а прибывает в 8:40 на следующий день (время московское). Сколько часов поезд находится в пути?
Ответ:________
4. В доме, в котором живёт Наташа, один подъезд. На каждом этаже по шесть квартир. Наташа живёт в квартире 52. На каком этаже живёт Наташа?
Ответ:________
5. При оплате услуг через платежный терминал взимается комиссия 3%. Терминал принимает суммы, кратные 10 рублям. Месячная плата за интернет составляет 550 рублей. Какую минимальную сумму положить в приемное устройство терминала, чтобы на счету фирмы, предоставляющей интернет-услуги, оказалась сумма, не меньшая 550 рублей?
Ответ:________
6. Студент получил свой первый гонорар в размере 1100 рублей за выполненный перевод. Он решил на все полученные деньги купить букет лилий для своей учительницы английского языка. Какое наибольшее количество лилий сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, лилии стоят 120 рублей за штуку и букет должен состоять из нечетного числа цветов?
Ответ:________
7. Одна таблетка лекарства весит 30 мг и содержит 7% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 0,6 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку в возрасте четырёх месяцев и весом 7 кг в течение суток?
Ответ:________
8. Диагональ экрана телевизора равна 50 дюймам. Выразите диагональ экрана в сантиметрах. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа.
Ответ:________
9. Бегун пробежал 150 м за 15 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
Ответ:________
10. В книге Елены Молоховец «Подарок молодым хозяйкам» имеется рецепт пирога с черносливом. Для пирога на 4 человек следует взять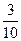 
фунта чернослива. Сколько граммов чернослива следует взять для пирога, рассчитанного на 5 человек? Считайте, что 1 фунт равен 0,4 кг.
Ответ:________
11. Одного рулона обоев хватает для оклейки полосы от пола до потолка шириной 1,2 м. Сколько рулонов обоев нужно купить для оклейки прямоугольной комнаты размерами 1,1 м на 5,8 м?
Ответ:________
Задание номер 2.
12. В ходе химической реакции количество исходного вещества (реагента), которое ещё не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат — масса оставшегося реагента, который ещё не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты?
Ответ:________
Задание номер 3.
13. На клетчатой бумаге с размером клетки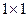 
изображён угол. Найдите тангенс этого угла.
Ответ:________
14. На клетчатой бумаге с размером клетки 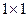изображён угол. Найдите тангенс этого угла.
Ответ:________
15. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры.
Ответ:________
16. На клетчатой бумаге с размером клетки 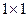отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC.
Ответ:________
17. На клетчатой бумаге с размером клетки 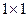изображён треугольник. Найдите радиус описанной около него окружности.
Ответ:________
18. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см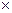 
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ:________
19. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 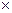1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ:________
Задание номер 4.
20. Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 46 теннисистов, среди которых 19 спортсменов из России, в том числе Ярослав Исаков. Найдите вероятность того, что в первом туре Ярослав Исаков будет играть с каким-либо теннисистом из России.
Ответ:________
21. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Ответ:________
22. На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,35. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Ответ:________
23. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Ответ:________
24. Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,07. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Ответ:________
25. Вероятность того, что новый пылесос прослужит больше года, равна 0,92. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Ответ:________
26. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 50% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 70% яиц высшей категории. Всего высшую категорию получает 65% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства
Ответ:________
27. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной и меньше 5?
Ответ:________
28. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Сапфир» выиграет жребий ровно один раз.
Ответ:________
29. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что наступит исход ОРР (в первый раз выпадает орёл, во второй и третий — решка).
Ответ:________
30. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, а при каждом последующем – 0,8. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Ответ:________
31. При изготовлении подшипников диаметром 65 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,981. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 64,99 мм, или больше, чем 65,01 мм.
Ответ:________
32. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 68 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Менеджмент», нужно набрать не менее 68 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент Р. получит не менее 68 баллов по математике, равна 0,7, по русскому языку — 0,7, по иностранному языку — 0,8 и по обществознанию — 0,5.
Найдите вероятность того, что Р. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Ответ:________
33. На фабрике керамической посуды 30% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 60% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Ответ:________
34. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стратор» по очереди играет с командами «Ротор», «Стартер» и «Протор». Найдите вероятность того, что «Стратор» будет начинать только вторую и последнюю игры.
Ответ:________
35. Фабрика выпускает сумки. В среднем на 45 качественных сумок приходится 5 сумок, имеющих скрытые дефекты. Найдите вероятность того, что выбранная в магазине сумка окажется с дефектами.
Ответ:________
36. За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
Ответ:________
37. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Ответ:________
Задание 5: уравнения.
38. Найдите корень уравнения 
.
Ответ: ______
39. Найдите корень уравнения 
.
Ответ: ______
40. Найдите корень уравнения 
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Ответ: ______
41. Найдите корень уравнения 
. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Ответ: ______
42. Найдите корень уравнения 
.
Ответ: ______
43. Найдите корень уравнения 
.
Ответ: ______
44. Найдите корень уравнения 
.
Ответ: ______
45. Найдите корень уравнения 
. В ответе запишите наименьший положительный корень.
Ответ: ______
46. Найдите корень уравнения 
. В ответе запишите наибольший отрицательный корень.
Ответ: ______
47. Найдите корень уравнения 
. В ответе запишите наибольший отрицательный корень.
Ответ: ______
48. Найдите корень уравнения 
.
Ответ: ______
49. Найдите корень уравнения 
.
Ответ: ______
50. Найдите корень уравнения 
.
Если уравнение имеет более одного корня, укажите меньший из них.
Ответ: ______
51. Найдите корень уравнения 
. В ответе запишите наибольший отрицательный корень.
Ответ: ______
52. Найдите корень уравнения 
. В ответе запишите наибольший отрицательный корень.
Ответ: ______
53. Найдите корень уравнения 
. В ответе запишите наименьший положительный корень.
Ответ: ______
54. Найдите корень уравнения 
.
Ответ: ______
55. Найдите корень уравнения 
.
Ответ: ______
56. Найдите корень уравнения 
. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Ответ: ______
57. Найдите корень уравнения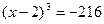 
.
Ответ: ______
58. Найдите корень уравнения 
.
Ответ: ______
59. Найдите корень уравнения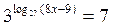 
.
Ответ: ______
Задание 6: простая планиметрия.
60. Площадь треугольника ABC равна 176. DE – средняя линия. Найдите площадь треугольника CDE.
Ответ: ______
61. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
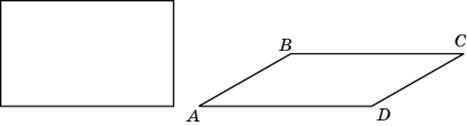
Ответ: ______
62. Стороны параллелограмма равны 40 и 80. Высота, опущенная на первую из этих сторон, равна 60. Найдите высоту, опущенную на вторую сторону параллелограмма.
Ответ: ______
63. Около окружности, радиус которой равен 4, описан многоугольник, периметр которого равен 63. Найдите его площадь.
Ответ: ______
64. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Ответ: ______
65. В треугольнике ABC угол B равен 9°, угол C равен 55°, AD – биссектриса, E — такая точка на AB, что AE = AC. Найдите угол BDE. Ответ дайте в градусах.
Ответ: ______
66. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 1:3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 50.
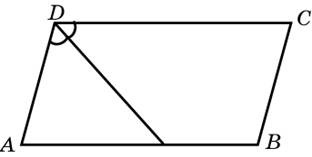
Ответ: ______
67. Основания трапеции равны 12 и 60. Найдите отрезок, соединяющий середины диагоналей трапеции.
Ответ: ______
68. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 36. Найдите ее среднюю линию.
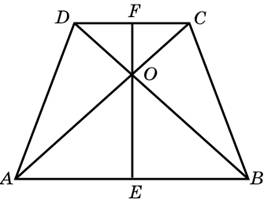
Ответ: ______
69. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 36. Найдите радиус описанной окружности этой трапеции.
Ответ: ______
70. Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 90°. Найдите число вершин многоугольника.
Ответ: ______
71. Катеты равнобедренного прямоугольного треугольника равны 
. Найдите радиус окружности, вписанной в этот треугольник.
Ответ: ______
72. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 32, 24. Найдите периметр данного треугольника.
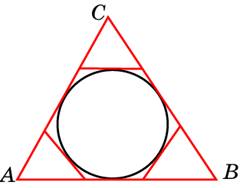
Ответ: ______
Задание 7.
73. На рисунке изображён график 
– производной функции 
, определенной на интервале 
. В какой точке отрезка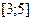 
функция принимает наибольшее значение?
Ответ: ______
74. На рисунке изображен график – производной функции , определенной на интервале 
. Найдите количество точек, в которых касательная к графику функции параллельна прямой 
или совпадает с ней.
Ответ: ______
75. На рисунке изображены график функции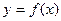 
и касательная к нему в точке с абсциссой 
. Найдите значение производной функции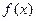 
в точке 
.
Ответ: ______
76. На рисунке изображены график функции 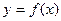и касательная к нему в точке с абсциссой . Найдите значение производной функции 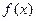в точке .
Ответ: ______
77. Прямая 
является касательной к графику функции 
. Найдите b, учитывая, что абсцисса точки касания меньше 0.
Ответ: ______
78. Материальная точка движется прямолинейно по закону 
, где 
– расстояние от точки отсчета в метрах,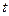 
– время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 93 м/с?
Ответ: ______
79. На рисунке изображён график функции 
– одной из первообразных функции 
, определённой на интервале 
. Найдите количество решений уравнения 
на отрезке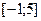 
.
Ответ: ______
80. На рисунке изображён график функции 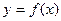(два луча с общей начальной точкой). Пользуясь рисунком, вычислите 
, где 
– одна из первообразных функции .
Ответ: ______
81. На рисунке изображён график некоторой функции 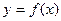. Функция 
– одна из первообразных функции 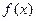. Найдите площадь закрашенной фигуры.
Ответ: ______
Задание 9. Значения выражений.
82. Найдите значение выражения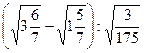 
.
Ответ: ______
83. Найдите значение выражения 
.
Ответ: ______
84. Найдите значение выражения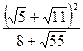 
.
Ответ: ______
85. Найдите значение выражения 
.
Ответ: ______
86. Найдите 
, если 
и 
.
Ответ: ______
87. Найдите 
, если 
.
Ответ: ______
88. Найдите 
, если 
.
Ответ: ______
89. Найдите 
, если 
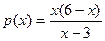при 
.
Ответ: ______
90. Найдите значение выражения 
при 
.
Ответ: ______
91. Найдите значение выражения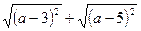 
при 
.
Ответ: ______
92. Найдите значение выражения 
при 
.
Ответ: ______
93. Найдите значение выражения 
.
Ответ: ______
94. Найдите значение выражения 
.
Ответ: ______
95. Найдите значение выражения 
.
Ответ: ______
96. Найдите значение выражения 
.
Ответ: ______
97. Найдите значение выражения 
.
Ответ: ______
98. Найдите значение выражения 
.
Ответ: ______
Задание 10.
99. При температуре 0°C рельс имеет длину 
м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону 
, где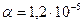 
(°C)-1 – коэффициент теплового расширения, 
– температура (в градусах Цельсия). При какой температуре рельс удлинится на 4,5 мм? Ответ выразите в градусах Цельсия.
Ответ: ______
100. Высота над землей подброшенного вверх мяча меняется по закону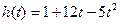 
, где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 5 метров?
Ответ: ______
101. Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому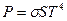 
, где P – мощность излучения звезды (в ваттах), 
– постоянная, S – площадь поверхности звезды (в квадратных метрах), а T – температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна 
м2, а мощность её излучения равна 
Вт. Найдите температуру этой звезды в кельвинах.
Ответ: ______
102. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием 
см. Расстояние 
от линзы до лампочки может изменяться в пределах от 50 до 70 см, а расстояние 
от линзы до экрана – в пределах от 160 до 180 см. Изображение на экране будет четким, если выполнено соотношение 
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах.
Ответ: ______
103. Перед отправкой тепловоз издал гудок с частотой 
Гц. Чуть позже гудок издал подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка 
больше первого: она зависит от скорости тепловоза по закону 
(Гц), где 
– скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 6 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а 
м/с. Ответ выразите в м/с.
Ответ: ______
104. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна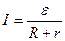 
, где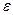 
– ЭДС источника (в вольтах), 
Ом – его внутреннее сопротивление, R – сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 5% от силы тока короткого замыкания 
? (Ответ выразите в омах).
Ответ: ______
105. Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле 
, где 
– частота вынуждающей силы (в с-1), 
– постоянный параметр, 
с-1 – резонансная частота. Найдите максимальную частоту 
, меньшую резонансной, для которой амплитуда колебаний превосходит величину 
не более чем на одну пятнадцатую. Ответ выразите в с-1.
Ответ: ______
106. Уравнение процесса, в котором участвовал газ, записывается в виде 
, где p (Па) – давление в газе, V – объем газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение в 16 раз объема газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 2 раза?
Ответ: ______
107. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением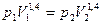 
, где p 1 и p 2 – давление газа (в атмосферах) в начальном и конечном состояниях, V 1 и V 2 – объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 64 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах
Ответ: ______
108. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону 
, где t – время в секундах, амплитуда U 0 = 2 В, частота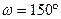 
/с, фаза 
. Датчик настроен так, что если напряжение в нём не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
Ответ: ______
109. Скорость колеблющегося на пружине груза меняется по закону 
(см/с), где t – время в секундах. Какую долю времени из первой секунды скорость движения превышала 4 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Ответ: ______
Задание 8: простая стереометрия.
110. Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.
Ответ: ______
111. Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна 
и образует с плоскостью этой грани угол 45°. Найдите объем параллелепипеда.
Ответ: ______
112. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с плоскостью этой грани угол 60° и равно 2. Найдите объем параллелепипеда.
Ответ: ______
113. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Ответ: ______
114. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см3.
Ответ: ______
115. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.
Ответ: ______
116. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Ответ: ______
117. Дано два цилиндра. Объём первого цилиндра равен 12. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра.
Ответ: ______
118. Объем конуса равен 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите объем отсеченного конуса.
Ответ: ______
Примечание: имеется в виду объём именно отсечённого конуса, который сверху, а не усечённого конуса, который снизу.
119. Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
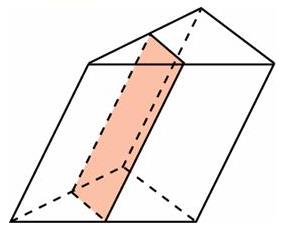
Ответ: ______
120. От треугольной пирамиды, объем которой равен 34, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Ответ: ______
121. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Ответ: ______
122. В правильной треугольной пирамиде боковое ребро равно 5, а сторона основания равна 
. Найдите высоту пирамиды.
Ответ: ______
123. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
Ответ: ______
124. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.
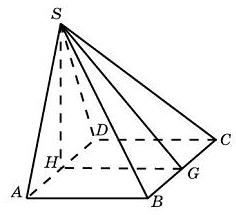
Ответ: ______
125. Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1.
Ответ: ______
Задание 11. Текстовые задачи.
126. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Ответ: ______
127. Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Ответ: ______
128. Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
Ответ: ______
129. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Ответ: ______
130. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?
Ответ: ______
131. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Ответ: ______
132. Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь — за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?
Ответ: ______
133. Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Ответ: ______
134. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Ответ: ______
135. Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 4,4 км от места отправления. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
Ответ: ______
136. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе