Способы определения натуральной величины отрезка

1. Способ вращения.

 

Необходимо повернуть отрезок вокруг одного из его концов, чтобы он расположился параллельно плоскости.

 

? По заданным координатам концов отрезка АВ построить его комплексный чертеж. Найти натуральную величину отрезка, пользуясь способом вращения.

 

 

№ варианта

Координаты

№ варианта

Координаты

А

В

А

В

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

 

2. Способ замены плоскостей.

 

Сводится к тому, что проецируемая линия остается на месте, а одну из плоскостей проекции заменяют дополнительной плоскостью, параллельной отрезку. На эту новую плоскость проецируют изображенный отрезок.

 

 

? По заданным координатам концов отрезка АВ построить комплексным чертеж. Найти натуральную величину отрезка, пользуясь способом замены плоскостей проекций.

№ варианта

Координаты

№ варианта

Координаты

А

В

А

В

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

 

4.3. Проецирование некоторых геометрических тел.

Детали машин, приборов и приспособлений часто имеют форму геометрических тел – призмы, пирамиды, цилиндра, конуса и т.п. Геометрические тела делят на две основные группы: многогранники и тела вращения. К многогранникам относят призмы и пирамиды, к телам вращения – цилиндр, конус, шар, тор.

 

Проекции поверхностей геометрических тел: а – призмы, б – пирамиды, в – цилиндра, г – конуса, д - шара

? Проанализируйте форму детали, мысленно расчленив ее на отдельные элементы. Какие геометрические тела образуют форму детали?

1. –

2. –

3. –

4. –

5. –

 

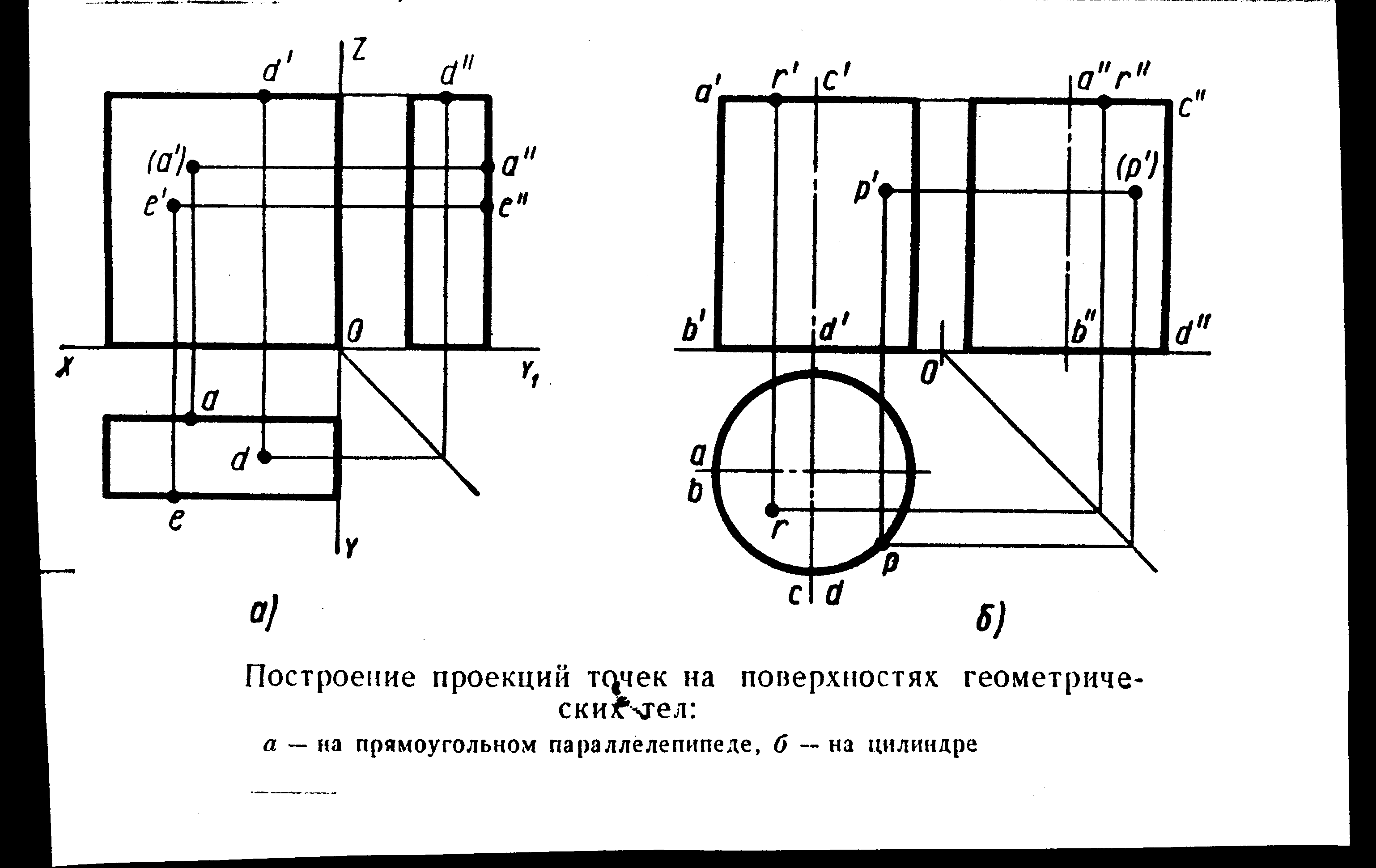4.4. Построение проекций точек, заданных на поверхности геометрических тел.

 

Построение проекций точек на поверхностях геометрических тел: а – на прямоугольном параллелепипеде, б – на шаре

 

 

? Прочитайте и нанесите точки на аксонометрическом изображении изделия кронштейна.

 

рис.44 Проекции точек на поверхностях модели (кронштейна)

На рис. 44,а показан кронштейн, состоящий из двух четырехугольных и одной треугольной призм. Требуется найти фронтальную и профильную проекции точки 4. Грань, на которой отмечена точка 4, перпендикулярна фронтальной и профильной плоскостям. Следовательно, проекции граней на эти плоскости будут изображены в виде линий, на которых и будут расположены фронтальная и профильная проекции точки 4 (44,б). Точка 2 расположена на наклонной грани треугольной призмы, поэтому найти проекцию точки 2 несколько сложнее. Наклонная грань призмы проецируется на профильную плоскость проекции в виде прямой линии. Следовательно, точку 2 необходимо сначала спроецировать на профильную плоскость, а затем – на фронтальную (главный вид). С этой целью на чертеже указаны линии проекционной связи.

Умение находить точки на проекциях и определять поверхности, на которых эти точки нанесены, позволяет устанавливать взаимное положение одной точки относительно другой, выделять, какая из точек расположена выше или ниже, какая из точек расположена ближе или дальше от наблюдателя.

 

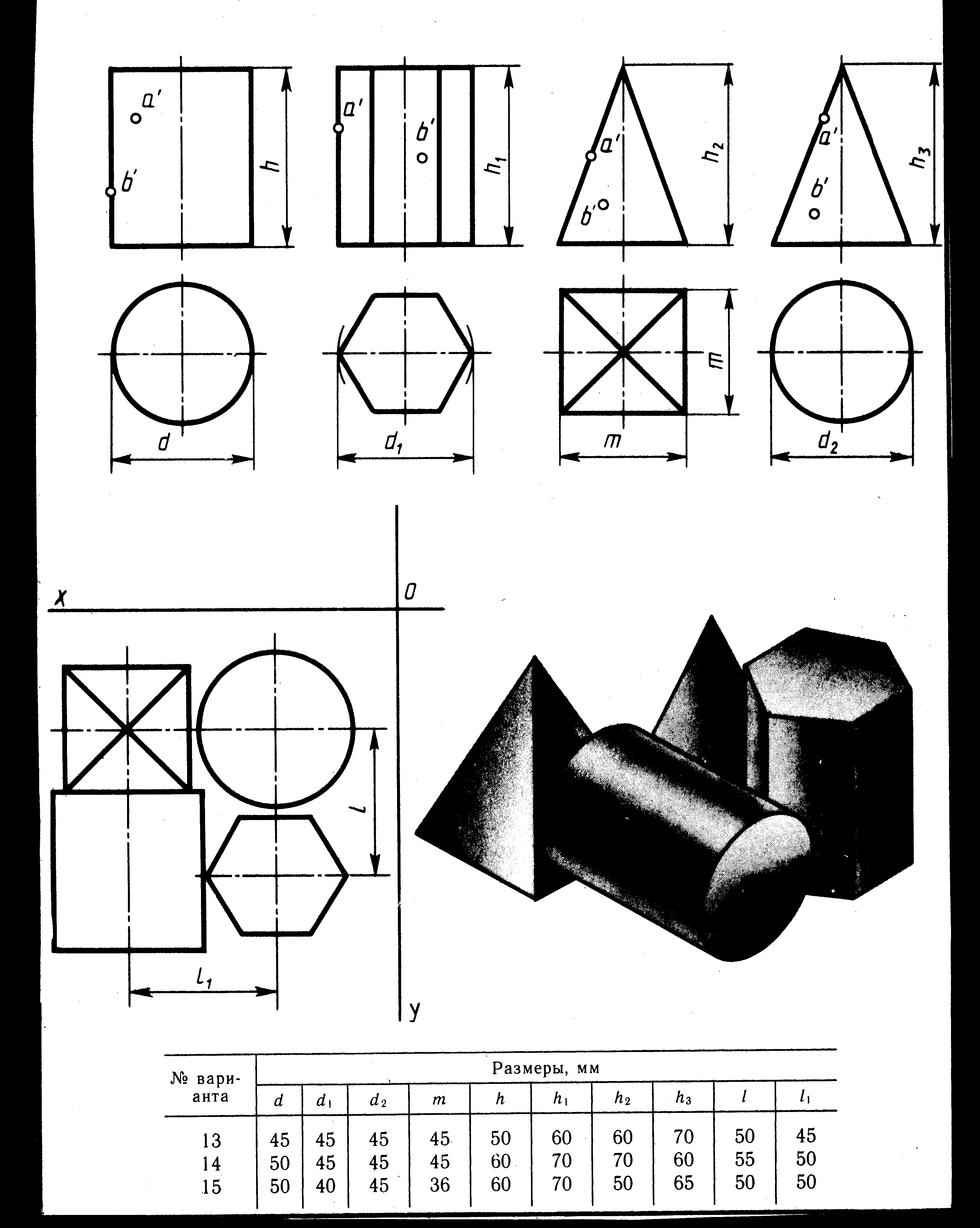
? Построить в трех проекциях геометрические тела (на чертеже сверху). Найти проекции точек, расположенных на их поверхностях. По выполненным чертежам построить аксонометрические проекции.

 

? По образцу построить в трех проекциях группу геометрических тел, взаимное расположение которых представлено на горизонтальной проекции и изометрической проекции (на чертеже снизу.)

 

 

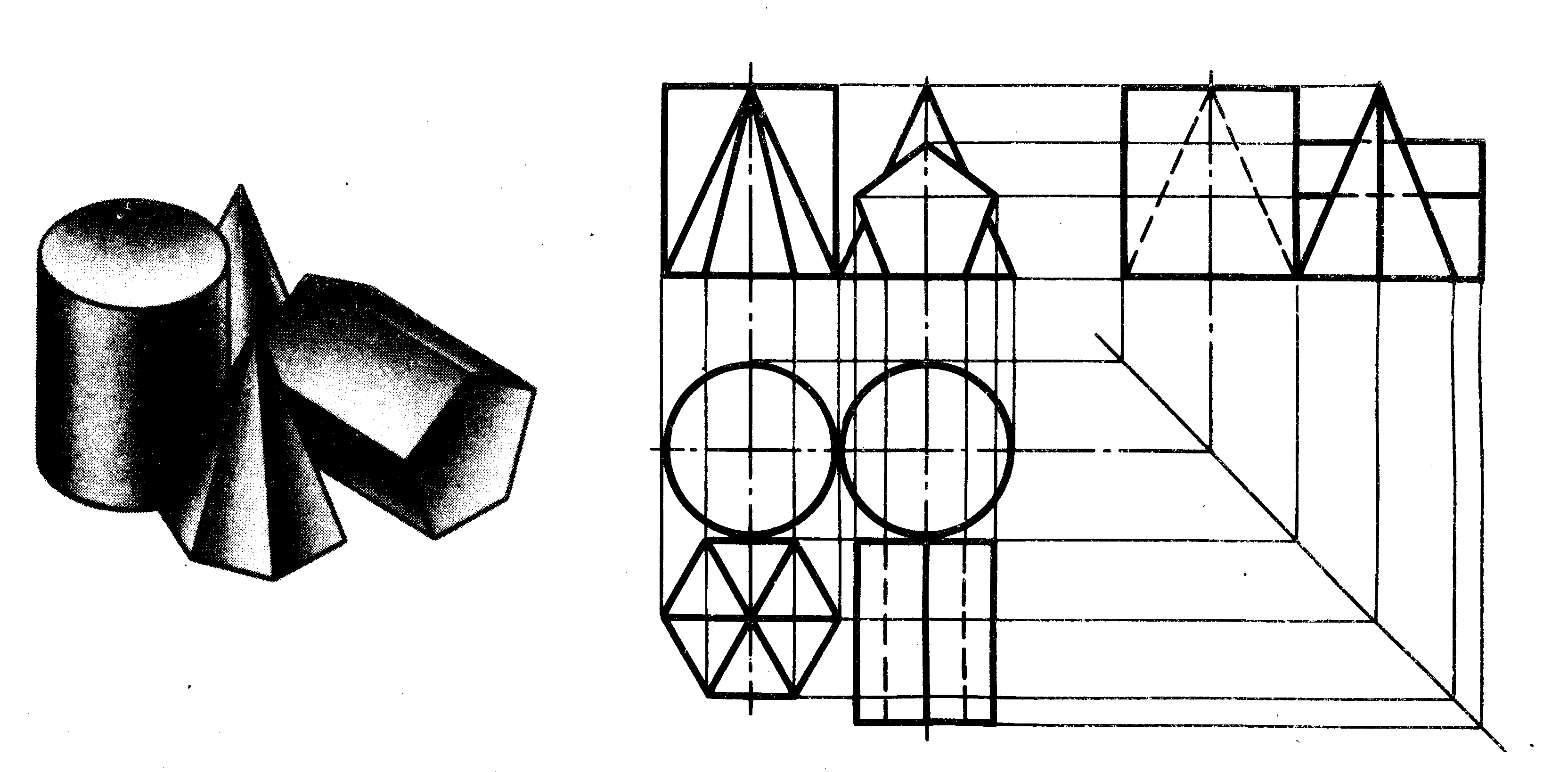
? Выполнить варианты с 1 по 15

 

Задание

 

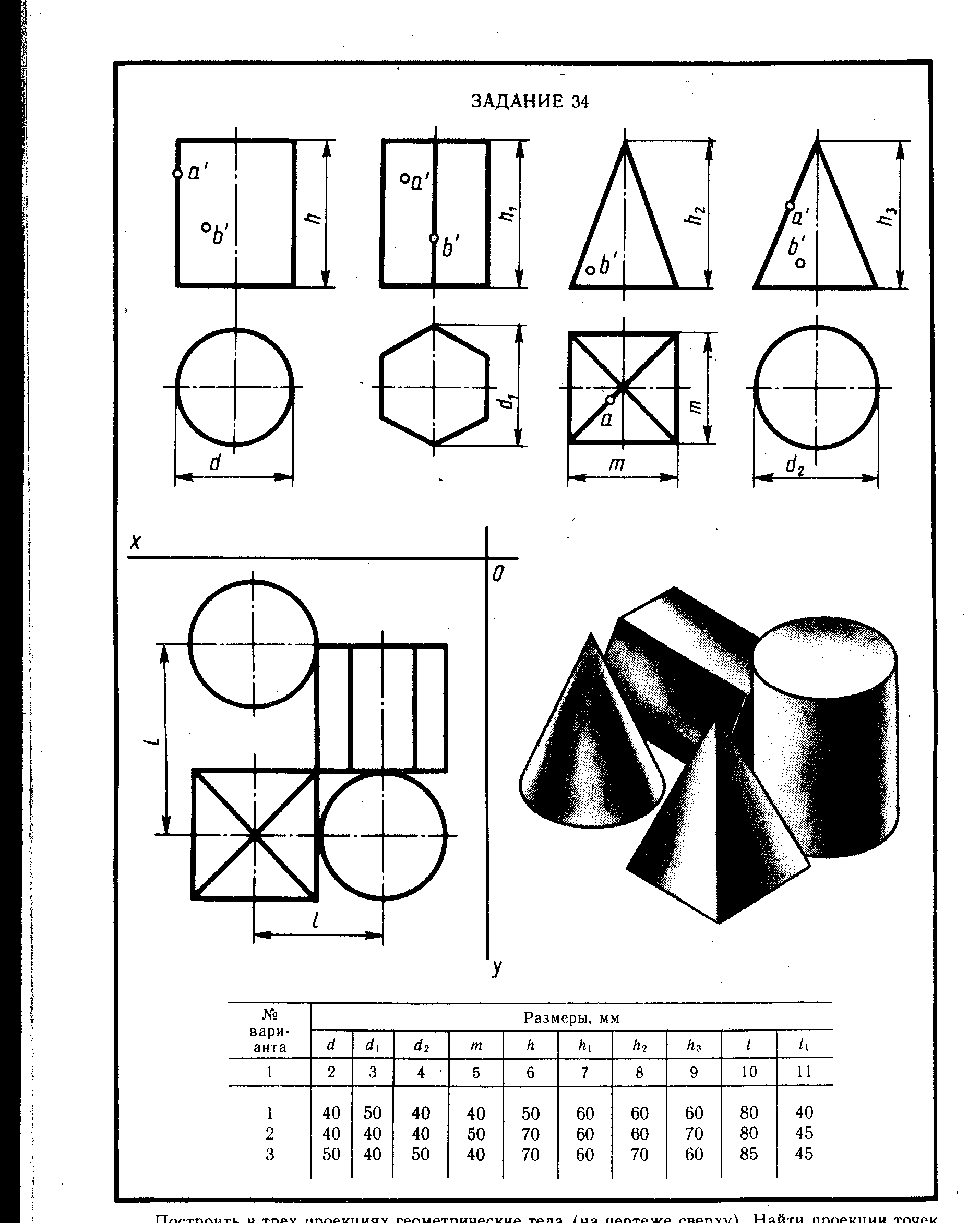
№ варианта	Размеры, мм
d	d1	d2	m	h	h1	h2	h3	l	l1

 

 

 

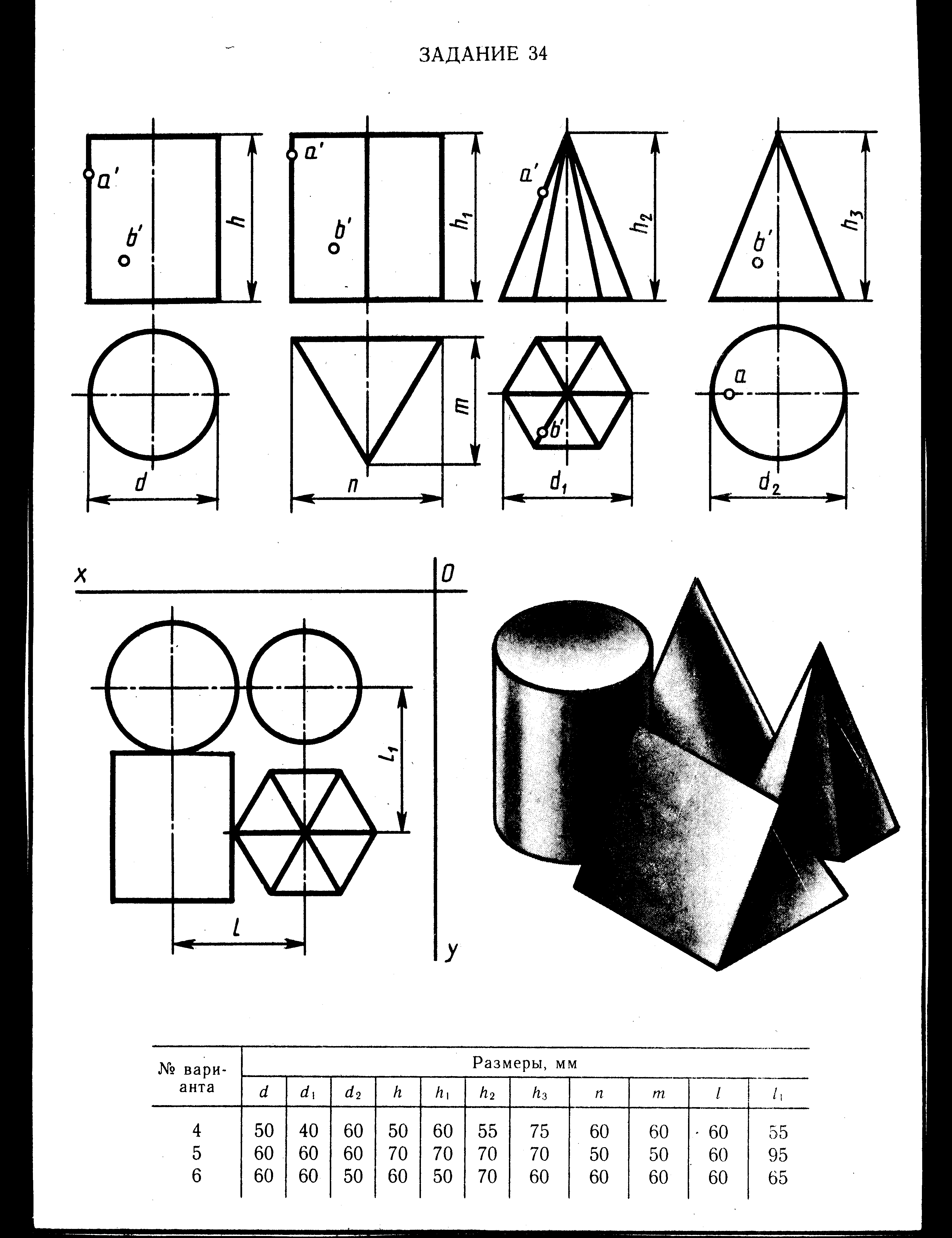
№ варианта	Размеры, мм
d	d1	d2	h	h1	h2	h3	n	m	l	l1

№ варианта	Размеры, мм
d	d1	d2	n	m	h	h1	h2	h3	l	l1

 

 

№ варианта	Размеры, мм
d	d1	d2	d3	d4	h	h1	h2	h3	l	l1

 

№ варианта	Размеры, мм
d	d1	d2	m	h	h1	h2	h3	l	l1