Другие важные свойства числовых неравенств

Числовые неравенства и их свойства.

 

Неравенства в математике играют заметную роль. В школе в основном мы имеем дело с числовыми неравенствами, с определения которых мы начнем эту статью. А дальше перечислим и обоснуем свойства числовых неравенств, на которых базируются все принципы работы с неравенствами.

Сразу отметим, что многие свойства числовых неравенств аналогичны свойствам числовых равенств. Поэтому, излагать материал будем по такой же схеме: формулируем свойство, приводим его обоснование и примеры, после чего переходим к следующему свойству.

Навигация по странице.

• Числовые неравенства: определение, примеры.
• Свойства числовых неравенств.
• Основные свойства.
• Другие важные свойства числовых неравенств.

 

Числовые неравенства: определение, примеры

Когда мы вводили понятие неравенства, то заметили, что неравенства часто определяют по виду их записи. Так неравенствами мы назвали имеющие смысл алгебраические выражения, содержащие знаки не равно ≠, меньше <, больше >, меньше или равно ≤ или больше или равно ≥. На основе приведенного определения удобно дать определение числового неравенства:

Определение.

Числовое неравенство – это неравенство, в записи которого по обе стороны от знака неравенства находятся числа или числовые выражения.

Встреча с числовыми неравенствами происходит на уроках математики в первом классе сразу после знакомства с первыми натуральными числами от 1 до 9, и знакомства с операцией сравнения. Правда, там их называют просто неравенствами, опуская определение «числовые». Для наглядности не помешает привести пару примеров простейших числовых неравенств из того этапа их изучения: 1<2, 5+2>3.

А дальше от натуральных чисел знания распространяются на другие виды чисел (целые, рациональные, действительные числа), изучаются правила их сравнения, и это значительно расширяет видовое разнообразие числовых неравенств: −5>−72, 3>−0,275·(7−5,6), .

К началу страницы

Свойства числовых неравенств

 

На практике работать с неравенствами позволяет ряд свойств числовых неравенств. Они вытекают из введенного нами понятия неравенства. По отношению к числам это понятие задается следующим утверждением, которое можно считать определением отношений «меньше» и «больше» на множестве чисел (его часто называют разностным определением неравенства):

Определение.

· число a больше числа b тогда и только тогда, когда разность a−b является положительным числом;

· число a меньше числа b тогда и только тогда, когда разность a−b – отрицательное число;

· число a равно числу b тогда и только тогда, когда разность a−b равна нулю.

Это определение можно переделать в определение отношений «меньше или равно» и «больше или равно». Вот его формулировка:

Определение.

· число a больше или равно числу b тогда и только тогда, когда a−b – неотрицательное число;

· число a меньше или равно числу b тогда и только тогда, когда a−b – неположительное число.

Данные определения мы будем использовать при доказательстве свойств числовых неравенств, к обзору которых мы и переходим.

К началу страницы

Основные свойства

Обзор начнем с трех основных свойств неравенств. Почему они основные? Потому, что они являются отражением свойств неравенств в самом общем смысле, а не только по отношению к числовым неравенствам.

Числовым неравенствам, записанным с использованием знаков < и >, характерно:

· Свойство антирефлексивности, выражающееся в том, что для любого числа a неравенства a<a и a>a – неверные.

Действительно, известно, что для любого числа a выполняется равенство a−a=0, откуда в силу разностного определения равных чисел следует равенство a=a. Следовательно, a<a и a>a – неверные неравенства.

Например, 3<3 и - неверные неравенства.

· Свойство антисимметричности: если числа a и b такие, что a<b, то b>a, и если a>b, то b<a.

Обоснуем его, обратившись к данному выше определению отношений «больше» и «меньше». Начнем с первой части. Так как a<b, то a−b – отрицательное число. При этом b−a=−(a−b) – положительное число, как число, противоположное отрицательному числу a−b. Следовательно, b>a. Аналогично доказывается и вторая часть рассматриваемого свойства.

Приведем пример: из неравенства 5<11 вытекает, что 11>5, а числовое неравенство −0,27>−1,3 можно переписать как −1,3<−0,27.

И перед переходом к следующему свойству заметим, что свойство антисимметричности позволяет читать неравенства как слева направо, так и справа налево. А точнее на его базе можно менять местами части числового неравенства, изменив при этом знак неравенства на противоположный (< на >, а > на <).

· Свойство транзитивности: если числа a, b и c таковы, что a<b и b<c, то a<c, и если a>b и b>c, то a>c.

Докажем его первое утверждение. Условия a<b и b<c означают, что a−b и b−c – отрицательные числа. Разность a−c можно представить как (a−b)+(b−c), а это есть отрицательное число как сумма двух отрицательных чисел a−b и b−c, что следует из правила сложения отрицательных чисел. Таким образом, a−c – отрицательное число, откуда следует, что a<c, что и требовалось доказать. Абсолютно аналогично доказывается и вторая часть свойства транзитивности.

Покажем примеры применения разобранного свойства неравенств. Например, из неравенств −1<5 и 5<8 можно заключить, что −1<8. Аналогично, из числовых неравенств и вытекает, что .

Что касается числовых неравенств, записанных при помощи знаков нестрогих неравенства ≤ и ≥, то они обладают свойством рефлексивности (а не антирефлексивности), так как неравенства a≤a и a≥a включают в себя случай равенства a=a. Также им свойственны антисимметричность и транзитивность.

Итак, числовые неравенства, записанные при помощи знаков ≤ и ≥, обладают свойствами:

· рефлексивности a≥a и a≤a – верные неравенства;

· антисимметричности, если a≤b, то b≥a, и если a≥b, то b≤a.

· транзитивности, если a≤b и b≤c, то a≤c, а также, если a≥b и b≥c, то a≥c.

Их доказательство очень похоже на уже приведенные, поэтому не будем на них останавливаться, а перейдем к другим важным свойствам числовых неравенств.

К началу страницы

Другие важные свойства числовых неравенств

Дополним основные свойства числовых неравенств еще серией результатов, имеющих большое практическое значение. На них основаны методы оценки значений выражений, на них базируются принципы решения неравенств и т.п. Поэтому целесообразно хорошо разобраться с ними.

В этом пункте свойства неравенств будем формулировать только для одного знака строгого неравенства, но стоит иметь в виду, что аналогичные свойства будут справедливы и для противоположного ему знака, а также для знаков нестрогих неравенств. Поясним это на примере. Ниже мы сформулируем и докажем такое свойство неравенств: если a<b и c – любое число, то a+c<b+c. Наряду с ним будут справедливы и такие свойства:

· если a>b, то a+c>b+c;

· если a≤b, то a+c≤b+c;

· если a≥b, то a+c≥b+c.

Для удобства представим свойства числовых неравенств в виде списка, при это будем давать соответствующее утверждение, записывать его формально с помощью букв, приводить доказательство, после чего показывать примеры использования. А в конце статьи сведем все свойства числовых неравенств в таблицу. Поехали!

· Прибавление (или вычитание) любого числа к обеим частям верного числового неравенства дает верное числовое неравенство. Другими словами, если числа a и b таковы, что a<b, то для любого числа c справедливо неравенство a+c<b+c.

Для доказательства составим разность левой и правой частей последнего числового неравенства, и покажем, что она отрицательна при условии a<b. Имеем (a+c)−(b+c)=a+c−b−c=a−b. Так как по условию a<b, то a−b<0. Следовательно, (a+c)−(b+c)<0, откуда a+c<b+c.

На доказательстве этого свойства числовых неравенств для вычитания числа c не останавливаемся, так как на множестве действительных чисел вычитание можно заменить прибавлением противоположного числа −c.

Например, если к обеим частям верного числового неравенства 7>3 прибавить число 15, то получится верное числовое неравенство 7+15>3+15, что то же самое, 22>18.

· Если обе части верного числового неравенства умножить (или разделить) на одно и то же положительное число c, то получится верное числовое неравенство. Если обе части неравенства умножить (или разделить) на отрицательное число c, и изменить знак неравенства на противоположный, то получится верное неравенство. В буквенном виде: если для чисел a и b выполняется неравенство a<b и c – положительное число, то a·c<b·c, а если c – отрицательное число, то a·c>b·c.

Доказательство. Начнем со случая, когда c>0. Составим разность левой и правой частей доказываемого числового неравенства: a·c−b·c=(a−b)·c. Так как по условию a<b, то a−b<0. А так как c>0, то произведение (a−b)·c будет отрицательным числом как произведение отрицательного числа a−b на положительное число c (что следует из правила умножения чисел с разными знаками). Следовательно, a·c−b·c<0, откуда a·c<b·c. Вторая часть утверждения для c<0 доказывается аналогично.

На доказательстве рассмотренного свойства для деления обеих частей верного числового неравенства на одно и то же число c не останавливаемся, так как деление всегда можно заменить умножением на обратное число 1/c.

Покажем пример применения разобранного свойства на конкретных числах. Например, можно обе части верного числового неравенства 4<6 умножить на положительное число 0,5, что дает верное числовое неравенство −4·0,5<6·0,5, откуда −2<3. А если обе части верного числового неравенства −8≤12 разделить на отрицательное число −4, и изменить знак неравенства ≤ на противоположный ≥, то получится верное числовое неравенство −8:(−4)≥12:(−4), откуда 2≥−3.

Из только что разобранного свойства умножения обеих частей числового равенства на число следуют два практически ценных результата. Так их и сформулируем в виде следствий.

o Следствие 1. Если изменить знаки обеих частей числового неравенства и знак самого неравенства, то придем к верному неравенству, то есть, если a<b, то −a>−b.

Данное следствие соответствует умножению обеих частей числового равенства на минус единицу. Оно обычно используется для перехода от неравенств, в которых фигурируют отрицательные числа, к неравенствам с положительными числами. Например, если −7<−1, то 7>1.

o Следствие 2. Если обе части числового равенства являются положительными числами, то, заменив их обратными им числами, и изменив знак неравенства на противоположный, будет получено верное числовое неравенство. То есть, если a и b – положительные числа, причем a<b, то .

Действительно, к последнему неравенству можно прийти, если обе части неравенства a<b разделить на положительное число a·b. Приведем пример использования данного свойства: из верного неравенства 5>3/2 следует неравенство . Здесь нужно подчеркнуть, что для отрицательных a или b при условии a<b неравенство может быть неверным. К примеру, −2<3, но 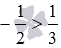- неверное равенство.

Все разобранные выше в этом пункте свойства объединяет то, что сначала дано верное числовое неравенство, и из него посредствам некоторых манипуляций с частями неравенства и знаком получается другое верное числовое неравенство. Сейчас мы приведем блок свойств, в которых изначально дано не одно, а несколько верных числовых неравенств, а новый результат получается из их совместного использования после сложения или умножения их частей.

· Если для чисел a, b, c и d справедливы неравенства a<b и c<d, то верным является и числовое неравенство a+c<b+d. Данное свойство числовых неравенств обычно формулируют в следующем виде: можно почленно складывать верные неравенства одного знака (под этим понимают, что все неравенства записаны с помощью одного знака, например, <, и под почленным сложением понимают сложение чисел, стоящих по одну сторону этого знака).

Докажем, что (a+c)−(b+d) – отрицательное число, этим будет доказано, что a+c<b+d. По условию a<b и c<d. Выше мы доказали свойство, позволяющее прибавлять к обеим частям числовых неравенств одно и то же число. Прибавим число c к обеим частям неравенства a<b, и число b – к обеим частям неравенства c<d, получаем a+c<b+c и b+c<b+d. Из полученных неравенств по свойству транзитивности заключаем, что a+c<b+d, что и требовалось доказать.

По индукции это свойство распространяется на почленное сложение трех, четырех, и, вообще, любого конечного числа числовых неравенств. Так, если для чисел a₁, a₂, …, a_n и b₁, b₂, …, b_n справедливы неравенства a₁<b₁, a₂<b₂, …, a_n<b_n, то методом математической индукции можно доказать, что a₁+a₂+…+a_n<b₁+b₂+…+b_n.

Например, нам даны три верных числовых неравенства одного знака −5<−2, −1<12 и 3<4. Рассмотренное свойство числовых неравенств позволяет нам констатировать, что неравенство −5+(−1)+3<−2+12+4 – тоже верное.

· Можно почленно умножать числовые неравенства одного знака, обе части которых представлены положительными числами. В частности, для двух неравенств a<b и c<d, где a, b, c и d – положительные числа справедливо числовое неравенство a·c<b·d.

Для доказательства можно умножить обе части неравенста a<b на число c, и обе части неравенства c<d – на число b, что дает верные числовые неравенства a·c<b·c и b·c<b·d, из которых по свойству транзитивности следует, что a·c<b·d.

Указанное свойство справедливо и для умножения любого конечного числа верных числовых неравенств с положительными частями. То есть, если a₁, a₂, …, a_n и b₁, b₂, …, b_n – положительные числа, причем a₁<b₁, a₂<b₂, …, a_n<b_n, то a₁·a₂·…·a_n<b₁·b₂·…·b_n.

Отдельно стоит заметить, что если в записи числовых неравенств содержатся неположительные числа, то их почленное умножение может приводить к неверным числовым неравенствам. Например, числовые неравенства 1<3 и −5<−4 – верные и одного знака, почленное умножение этих неравенств дает 1·(−5)<3·(−4), что то же самое, −5<−12, а это неверное неравенство.

o Следствие. Почленное умножение одинаковых верных неравенств вида a<b с положительными a и b дает верное числовое неравенство aⁿ<bⁿ.

В заключение статьи, как и было обещано, соберем все изученные свойства в таблицу свойств числовых неравенств: