Аддитивная и мультипликативная модели временного ряда

Моделирование колебаний

Моделирование сезонных и циклических колебаний

Аддитивная и мультипликативная модели временного ряда

Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания. Моделирование циклических колебаний в целом осуществляется аналогично моделированию сезонных колебаний, поэтому мы рассмотрим только методы моделирования последних.

Простейший подход – расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда. Общий вид аддитивной модели следующий:

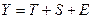
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой , сезонной и случайной компонент. Общий вид мультипликативной модели выглядит так:

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой, сезонной и случайной компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значений , и для каждого уровня ряда. Процесс построения модели включает в себя следующие шаги.

1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты .
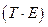3. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной или в мультипликативной модели.
4. Аналитическое выравнивание уровней или 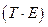и расчет значений с использованием полученного уравнения тренда.
5. Расчет полученных по модели значений или .
6. Расчет абсолютных и/или относительных ошибок.

Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.

Подробнее методику построения каждой из моделей рассмотрим на примерах.

Пример 3. Построение аддитивной модели временного ряда.

Обратимся к данным об объеме потребления электроэнергии жителями района за последние четыре года, представленным в табл. 3.

В примере 2 было показано, что данный временной ряд содержит сезонные колебания периодичностью 4. Объемы потребления электроэнергии в осенне-зимний период времени (I и IV кварталы) выше, чем весной и летом (II и III кварталы). По графику этого ряда можно установить наличие приблизительно равной амплитуды колебаний. Это свидетельствует о возможном существовании в ряде аддитивной модели. Рассчитаем ее компоненты.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого найдем уже центрированные четырехчленные скользящие средние по формулам: , и т.д.

Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними.

Таблица 5

Расчет оценок сезонной компоненты в аддитивной модели

№ квартала	Потребление электроэнергии	Центрированная скользящая средняя	Оценка сезонной компоненты
	6,0
	4,4
	5,0	6,250	-1,250
	9,0	6,450	2,550
	7,2	6,625	0,575
	4,8	6,875	-2,075
	6,0	7,100	-1,100
	10,0	7,300	2,700
	8,0	7,450	0,550
	5,6	7,625	-2,025
	6,4	7,875	-1,475
	11,0	8,125	2,875
	9,0	8,325	0,675
	6,6	8,375	-1,775
	7,0
	10,8

Используем эти оценки для расчета значений сезонной компоненты (табл. 6). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю .

Для данной модели имеем: .

Определим корректирующий коэффициент:

.

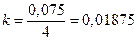Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом :

.

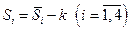Таблица 6