Задача 1. Найти производную функции одной переменной, исходя из определения производной.
Решение типового варианта
Задание. Используя определение производной, найти производные функции:
а)  б)
б)  в)
в) 
Решение.
а) Дадим аргумент х приращение  и найдем наращенное значение функции:
и найдем наращенное значение функции:

Находим приращение функции:

Составляем отношение:

Находим предел:

Итак, получим:

б) Произведем операции по указанной схеме:





в) 





Расчетные задания
1.1.  1.2.
1.2.  1.3.
1.3. 
1.4.  1.5.
1.5.  1.6.
1.6. 
1.7.  1.8.
1.8.  1.9.
1.9. 
1.11. 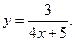 1.11.
1.11.  1.12.
1.12. 
1.13.  1.14.
1.14.  1.15.
1.15. 
1.16.  1.17.
1.17.  1.18.
1.18. 
1.19.  1.20.
1.20.  1.21.
1.21. 
1.22.  1.23.
1.23.  1.24.
1.24. 
1.25.  1.26.
1.26.  1.27.
1.27. 
1.28.  1.29.
1.29.  1.30.
1.30. 
Задача 2. Продифференцировать данные функции (в первом примере найти y / и y / /).
Решение типового варианта
Задание. Продифференцировать функции:
а) 

Решение.
а) Для упрощения операции дифференцирования перейдем в функции к дробным и отрицательным показателям.

Используя правило дифференцирования степени  , получим:
, получим:


б) Используем правило дифференцирования сложной степенной функции 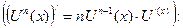



Расчетные задания
2.1 а)  б)
б) 
2.2. а)  б)
б) 
2.3. а)  б)
б) 
2.4. а)  б)
б) 
2.5. а)  б)
б) 
2.6. а)  б)
б) 
2.7. а)  б)
б) 
2.8. а)  б)
б) 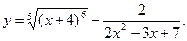
2.9. а)  б)
б) 
2.10. а)  б)
б) 
2.11. а)  б)
б) 
2.12. а)  б)
б) 
2.13. а)  б)
б) 
2.14. а)  б)
б) 
2.15. а)  б)
б) 
2.16. а)  б)
б) 
2.17. а)  б)
б) 
2.18. а)  б)
б) 
2.19. а)  б)
б) 
2.20. а) 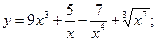 б)
б) 
2.21. а)  б)
б) 
2.22. а)  б)
б) 
2.23. а) 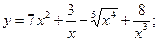 б)
б) 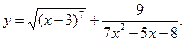
2.24. а)  б)
б) 
2.25. а)  б)
б) 
2.26. а)  б)
б) 
2.27. а)  б)
б) 
2.28. а)  б)
б) 
2.29. а)  б)
б) 
2.30. а)  б)
б) 
Задача 3. Найти производные первого порядка данных функций, используя правила вычисления производных.
Решение типового варианта
Задание. Используя правила дифференцирования, найти производные первого порядка от функций:
а)  б)
б) 
в)  г)
г) 
Решение.
а) 
б) Данная функция представляет произведение двух функций е3х и cos2x, каждая из которой является сложной функцией 
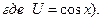 Поэтому, согласно правилу дифференцирования произведения, имеем:
Поэтому, согласно правилу дифференцирования произведения, имеем:


в) По правилу дифференцирования частного двух функций имеем:


г) Используем правило дифференцирования функций, заданной параметрически. Тогда

Итак, получаем:

Расчетные задания
3.1. а)  б)
б) 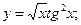
в)  г)
г) 
3.2. а) 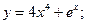 б)
б) 
в)  г)
г) 
3.3. а)  б)
б) 
в)  г)
г) 
3.4. а)  б)
б) 
в)  г)
г) 
3.5. а)  б)
б) 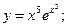
в)  г)
г) 
3.6. а)  б)
б) 
в) 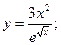 г)
г) 
3.7. а)  б)
б) 
в)  г)
г) 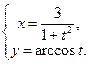
3.8. а)  б)
б) 
в) 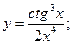 г)
г) 
3.9. а)  б)
б) 
в)  г)
г) 
3.10. а)  б)
б) 
в)  г)
г) 
3.11. а)  б)
б) 
в) 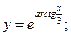 г)
г) 
3.12. а)  б)
б) 
в)  г)
г) 
3.13. а)  б)
б) 
в)  г)
г) 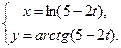
3.14. а)  б)
б) 
в)  г)
г) 
3.15. а) 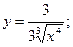 б)
б) 
в) г) 
3.16. а)  б)
б) 
в)  г)
г) 
3.17. а)  б)
б) 
в)  г)
г) 
3.18. а)  б)
б) 
в)  г)
г) 
3.19. а)  б)
б) 
в)  г)
г) 
3.20. а)  б)
б) 
в) 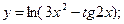 г)
г) 
3.21. а)  б)
б) 
в)  г)
г) 
3.22. а)  б)
б) 
в)  г)
г) 
3.23. а)  б)
б) 
в) 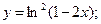 г)
г) 
3.24. а)  б)
б) 
в)  г)
г) 
3.25. а)  б)
б) 
в)  г)
г) 
3.26. а)  б)
б) 
в)  г)
г) 
3.27. а)  б)
б) 
в)  г)
г) 
3.28. а) 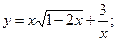 б)
б) 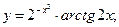
в)  г)
г) 
3.29. а)  б)
б) 
в)  г)
г) 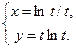
3.30. а) 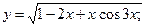 б)
б) 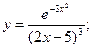
в) 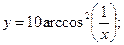 г)
г) 
Задача 4. Найти производные данных функций, предварительно прологарифмировав выражение.
Решение типового варианта
Задание. Продифференцировать функцию

Решение.
Предварительно прологарифмируем функцию


Дифференцируем обе части последнего равенства по x:

Отсюда

Далее выражаем  :
:

Окончательно получим:

Расчетные задания
4.1.  4.2.
4.2. 
4.3. 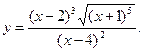 4.4.
4.4. 
4.5.  4.6.
4.6. 
4.7.  4.8.
4.8. 
4.9. 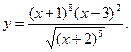 4.10.
4.10. 
4.11. 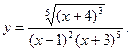 4.12.
4.12. 
4.13.  4.14.
4.14. 
4.15.  4.16.
4.16. 
4.17.  4.18.
4.18. 
4.19.  4.20.
4.20. 
4.21.  4.22.
4.22. 
4.23.  4.24.
4.24. 
4.25.  4.26.
4.26. 
4.27.  4.28.
4.28. 
4.29.  4.30.
4.30. 
Задача 5. составить уравнение касательной и нормали к графику кривой  в точке, абсцисса которой равна х0.
в точке, абсцисса которой равна х0.
Решение типового варианта
Задание. Записать уравнение касательной и нормали к графикам функций:
а)  б)
б)  в точке
в точке
абсцисса которой х0 =1.
Решение.
а) Для составления уравнения касательной согласно формуле  к данному графику функции находим ординату точки касания:
к данному графику функции находим ординату точки касания:
 ;
;
угловой коэффициент касательной равен:

Записываем уравнение касательной к графику в точке (1;4):
 или
или 
Используя полученные данные, записываем уравнение нормали согласно формуле

Тогда имеем
 или
или 
б) Находим ординату точки касания

и угловой коэффициент касательной

Уравнение касательной имеет вид:
 или
или 
Уравнение нормали будет:
 или
или 
Расчетные задания
5.1. 

5.2. 

5.3 

5.4. 

5.5. 

5.6. 

5.7. 

5.8. 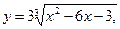

5.9. 

5.10. 

5.11. 

5.12. 

5.13. 

5.14. 

5.15. 

5.16. 

5.17. 

5.18. 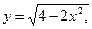

5.19. 

5.20. 

5.21. 

5.22. 

5.23. 

5.24. 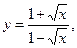

5.25. 

5.26. 

5.27. 

5.28. 

5.29. 

2.30. 

Задача 6. Вычислить предел функций с помощью правил Лопиталя.
Решение типового варианта
Задание. Вычислить предел функций с помощью правила Лопиталя:
а)  б)
б) 
Решение.
а) Под знаком предела числитель и знаменатель дроби стремятся к нулю при 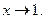 Приходим к неопределенности типа
Приходим к неопределенности типа  Для раскрытия ее применим правило Лопиталя:
Для раскрытия ее применим правило Лопиталя:
б) В данном случае имеем неопределенность  к раскрытию которой правило Лопиталя не применимо. Преобразуем выражение к тому виду, чтобы получилась неопределенность
к раскрытию которой правило Лопиталя не применимо. Преобразуем выражение к тому виду, чтобы получилась неопределенность 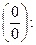

Получим неопределенность вида  к раскрытию которой применим правило Лопиталя:
к раскрытию которой применим правило Лопиталя:

Получим снова неопределенное выражение типа  Повторно применив правило Лопиталя, получим:
Повторно применив правило Лопиталя, получим:

Еще раз применив это правило, будем иметь:

Расчетные задания
6.1.  6.2.
6.2. 
6.3.  6.4.
6.4. 
6.5.  6.6.
6.6. 
6.7.  6.8.
6.8. 
6.9. 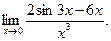 6.10.
6.10. 
6.11.  6.12.
6.12. 
6.13.  6.14.
6.14. 
6.15.  6.16.
6.16. 
6.17.  6.18.
6.18. 
6.19. 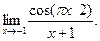 6.20.
6.20. 
6.21.  6.22.
6.22. 
6.23.  6.24.
6.24. 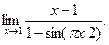
6.25.  6.26.
6.26. 
6.27.  6.28.
6.28. 
6.29.  6.30.
6.30. 