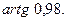Задача 7. Построить график функции с помощью производной первого порядка.
Указание. При построении графика функции с помощью первой производной предлагаем придерживаться следующей схеме:
1) найти область определения функции, если она заранее не указана;
2) проверить функцию на четность и нечетность;
3) исследовать функцию на периодичность;
4) найти точки пересечения графика функции с осями координат;
5) найти интервал знакопостоянства функции;
6) найти асимптоты графика функции;
7) исследовать функцию на монотонность и отметить интервалы возрастания и убывания;
8) найти абсциссы точек экстремума функции и ее экстремальные значения.
Согласно данным исследованиям стоим эскиз графика функции.
Решение типового варианта
Задание. Построить график функции  с помощью производной первого порядка.
с помощью производной первого порядка.
Решение.
1. Функция  определена для любого
определена для любого 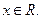
2. Функция четная, т.к. область определения условие 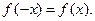 График функции симметричен относительно оси ординат.
График функции симметричен относительно оси ординат.
3.Функция непериодическая.
4.Абсциссы точек пересечения графика функции с осями координат находим из уравнения  . Имеем:
. Имеем:  Им соответствует ордината
Им соответствует ордината 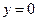 . Следовательно, график функций пересекает оси координат в следующих точках:
. Следовательно, график функций пересекает оси координат в следующих точках: 
5. Для нахождения интервалов, на которых функция принимает значения определенного знака, решим методом интервалов неравенство:
 или
или 
Для этого находим корни уравнения  Имеем
Имеем  Эти точки разбивают числовую прямую на четыре интервала:
Эти точки разбивают числовую прямую на четыре интервала:




Найдем знаки функции лишь на интервалах 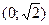 и
и  На втором интервале выполняется указанное неравенство, на первом – ему противоположное.
На втором интервале выполняется указанное неравенство, на первом – ему противоположное.
Следовательно,
 для всех
для всех 
 для всех
для всех 
В силу четности данной функции имеем:
 для всех
для всех 
 для всех
для всех 
6. У графика функции асимптот нет.
7. Найдем производную:  Она равна нулю в точках
Она равна нулю в точках 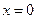 и
и 
Используем знак производной в окрестности каждой стационарной точки. Вследствие четности  достаточно установить знак
достаточно установить знак 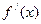 на промежутках (0;1) и (1;+¥).
на промежутках (0;1) и (1;+¥).
Взяв пробные точки, лежащие внутри этих промежутков убеждаемся, что для 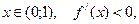 а для
а для 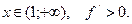 Поэтому на первом промежутке функция
Поэтому на первом промежутке функция  убывает, а на втором – возрастает. В силу четности функция для
убывает, а на втором – возрастает. В силу четности функция для 
 убывает, а для
убывает, а для 
 возрастает. В точках х= -1 и
возрастает. В точках х= -1 и
х = она принимает минимальное значение 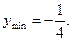 В точке х = 0 она принимает максимальное значение
В точке х = 0 она принимает максимальное значение  Используя результаты исследований, строим эскиз графика функции.
Используя результаты исследований, строим эскиз графика функции.
Расчетные задания
7.1. 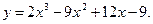 7.2.
7.2. 
7.3. 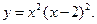 7.4.
7.4. 
7.5. 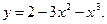 7.6.
7.6. 
7.7. 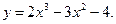 7.8.
7.8. 
7.9. 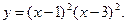 7.10
7.10 
7.11. 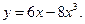 7.12.
7.12. 
7.13.  7.14.
7.14. 
7.15.  7.16.
7.16. 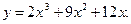
7.17.  7.18.
7.18. 
7.19.  7.20.
7.20. 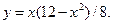
7.21.  7.22.
7.22. 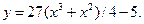
7.23.  7.24.
7.24. 
7.25.  7.26.
7.26. 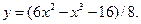
7.27. 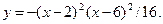 7.28.
7.28. 
7.29. 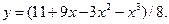 7.30.
7.30. 
Задача 8. Провести полное исследование функций и построить их графики.
Указание. Для полного исследования функции ко всем перечисленным ране пунктам добавляем пункт, включающий определение интервалов выпуклости и точек перегиба графика функции.
Решение типового варианта
Задание. Провести полное исследование функции  и построить ее график.
и построить ее график.
Решение.
1. Область определения функции – вся числовая прямая, кроме точек

2.  - нечетная функция, так как
- нечетная функция, так как 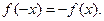 Поэтому для построения графика
Поэтому для построения графика  достаточно исследовать ее для
достаточно исследовать ее для 
3. Функция непериодическая.
4. График функции пересекает координат только в точке (0:0).
Точки  и
и  разбивают числовую прямую на четыре интервала:
разбивают числовую прямую на четыре интервала:

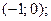


Найдем знаки функции лишь в интервалах  и
и 
 для всех
для всех 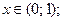
 для всех
для всех 
В силу нечетности данной функции имеем:
 для всех
для всех 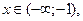
 для всех
для всех 
6. Так как
 и
и 
то прямые x= 1 и х= -1 являются вертикальными асимптотами. А так как


то график данной функции имеет асимптоту y = x.
7-8. Найдем производную: 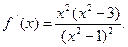 Она существует во всех точках числовой прямой, кроме
Она существует во всех точках числовой прямой, кроме  и равна нулю в точках х = 0 и
и равна нулю в точках х = 0 и  . Поэтому критическими будут следующие точки:
. Поэтому критическими будут следующие точки:



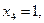

Изучим поведение 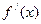 в окрестности каждой критической точки. Вследствие нечетности
в окрестности каждой критической точки. Вследствие нечетности  достаточно рассмотреть знак
достаточно рассмотреть знак 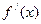 на промежутках (-1; 0), (0; 1), (1;
на промежутках (-1; 0), (0; 1), (1;  ) и (
) и ( ). Результаты исследования запишем в табл. 1.
). Результаты исследования запишем в табл. 1.
Таблица 1

| 
| 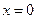
| 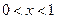
| 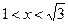
| 
| 
|
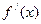
| - | - | - | - | + | |

| убывает | нет экстремума | убывает | убывает | минимум

| возрастает |
В точках х =-1 и х =1 функция не имеет экстремума, так как эти точки не принадлежат области определения данной функции.
В силу нечетности функции можно утверждать, что при  данная функция имеет максимум,
данная функция имеет максимум, 
9. Чтобы исследовать график функции на выпуклость, найдем вторую производную:
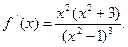
Критические точки данной функции (по второй производной) будут
 при х=0 и
при х=0 и 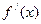 не существуют при
не существуют при  .
.
Однако точки  не принадлежат области определения функции, поэтому точка перегиба может быть только в точке с абсциссой х = 0.
не принадлежат области определения функции, поэтому точка перегиба может быть только в точке с абсциссой х = 0.
Исследуем знак второй производной. Результаты исследования запишем в табл. 2.
Таблица 2

| 
| 
| 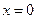
| 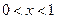
| 
|
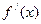
| - | + | - | + | |

| выпуклость вверх | выпуклость вниз | точка перегиба | выпуклость вверх | выпуклость вниз |
На основе приведенного исследования функции строим ее график (рис.2).
Расчетные задания
8.1. 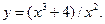 8.2.
8.2. 
8.3.  8.4.
8.4. 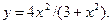
8.5.  8.6.
8.6. 
8.7. 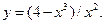 8.8.
8.8. 
8.9.  8.10.
8.10. 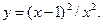
8.11.  8.12.
8.12. 
8.13.  8.14.
8.14. 

8.15.  8.16.
8.16. 
8.17.  8.18.
8.18. 
8.19. 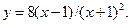 8.20.
8.20. 
8.21.  8.22.
8.22. 
8.23.  8.24.
8.24. 
8.25. 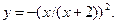 8.26.
8.26. 
8.27.  8.28.
8.28. 
8.29.  8.30.
8.30. 
Задание. Найти наибольшее и наименьшее значнения функции на заданных отрезках.
Указание. При нахождении наибольшего и наименьшего значений неприрывной функции  на отрезке [a; b] предлагаем придерживаться следующей схемы:
на отрезке [a; b] предлагаем придерживаться следующей схемы:
- найти 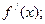

- найти точки, в которых  или
или 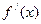 не существует, и отобразить из них те, которые лажат внутри отрезка [a; b];
не существует, и отобразить из них те, которые лажат внутри отрезка [a; b];
- вычислить значения функции  в точках, полученных в п. 2, а также на концах отрезка, и выбрать из них наибольшее и наименьшее: они являются соответственно наибольшим
в точках, полученных в п. 2, а также на концах отрезка, и выбрать из них наибольшее и наименьшее: они являются соответственно наибольшим 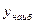 и наименьшим
и наименьшим  значением функции на отрезке [a; b].
значением функции на отрезке [a; b].
Решение типового варианта
Задание. Найти наибольшее и наименьшее значения функции:
а)  на отрезке [0; 6];
на отрезке [0; 6];
б)  на отрезке [0; 3].
на отрезке [0; 3].
Решение.
а) Найдем производную функцию:

Далее находим точки, в которых 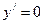 . Имеем:
. Имеем:
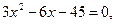



Отрезку [0; 6] принадлежат лишь точка 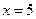
Вычисляем значение функции в точках 

Наибольшим из найденных значений функции является число 225, наименьшим – число 50.
Итак, 

 б) Производная данной функции равна
б) Производная данной функции равна
 если
если  то есть, когда
то есть, когда

Производная не существует, если 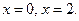
Вычислим значение функции в точках 0, 1, 2, 3:

т.е. 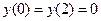 - наименьшее,
- наименьшее,  - наибольшее.
- наибольшее.
Расчетные задания
9.1. 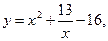 [1, 4].
[1, 4].
9.2 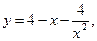 [1; 4].
[1; 4].
9.3. 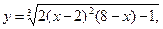 [0; 6].
[0; 6].
9.4. 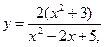 [-3; 3].
[-3; 3].
9.5.  [0; 4].
[0; 4].
9.6. 
 [-1; 5].
[-1; 5].
9.7. 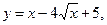 [1; 9].
[1; 9].
9.8. 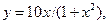 [0; 3].
[0; 3].
9.9.  [-3; 3].
[-3; 3].
9.10.  [2; 4].
[2; 4].
9.11.  [-1; 2].
[-1; 2].
9.12.  [-1; 6].
[-1; 6].
9.13.  [1; 4].
[1; 4].
9.14.  [-1; 7].
[-1; 7].
9.15.  [1; 5].
[1; 5].
9.16.  [-4; 2].
[-4; 2].
9.17. 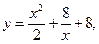 [-4; -1].
[-4; -1].
9.18.  [-2; 4].
[-2; 4].
9.19.  [-2; 1].
[-2; 1].
9.20.  [-5; 1].
[-5; 1].
9.21.  [0; 4].
[0; 4].
9.22. 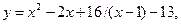 [2; 5].
[2; 5].
9.23. 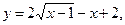 [1; 5].
[1; 5].
9.24.  [-3; 4].
[-3; 4].
9.25.  [-2; 1].
[-2; 1].
9.26. 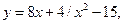 [1/2; 2].
[1/2; 2].
9.27.  [-4; 2].
[-4; 2].
9.28.  [-1; 2].
[-1; 2].
9.29.  [-2; -1/2].
[-2; -1/2].
9.30. 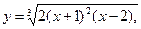 [-2; 5].
[-2; 5].
Задача 10. С помощью дифференциала приближено вычислить величины и оценить допущенную относительную погрешность (с точностью до двух знаков после запятой).
Решение типового варианта
Задание. С помощью дифференциала приближенно вычислить величину  и оценить допущенную относительную погрешность (с точностью до двух знаков после запятой).
и оценить допущенную относительную погрешность (с точностью до двух знаков после запятой).
Решение.
Введем в рассмотрение функцию 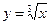 , где
, где 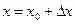 . Выберем
. Выберем  близкое к числу 84, из которого точно вычисляется кубический корень. Тогда, если принять
близкое к числу 84, из которого точно вычисляется кубический корень. Тогда, если принять  , то
, то  . Используя формулу
. Используя формулу  получим
получим
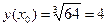 ,
, 
Вычисляем величину А:
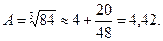
Относительная погрешность вычислений будет:

Расчетные задания
10.1.  10.2.
10.2. 
10.3.  10.4.
10.4. 
10.5.  10.6.
10.6. 
10.7.  10.8.
10.8. 
10.9. 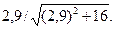 10.10.
10.10. 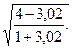
10.11.  10.12.
10.12. 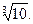
10.13.  10.14.
10.14. 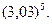
10.15.  10.16.
10.16. 
10.17.  10.18.
10.18. 
10.19.  10.20.
10.20. 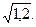
10.21.  10.22.
10.22. 
10.23 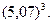 10.24.
10.24. 
10.25. 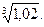 10.26.
10.26. 
10.27.  10.28.
10.28. 
10.29. 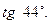 10.30.
10.30.