Описание модели РИВ
Реактор идеального вытеснения представляет собой длинный канал, через который реакционная смесь движется в поршневом режиме, при котором каждый ограниченный двумя плоскостями перпендикулярными оси потока элемент не смешивается ни с предыдущими ни с последующими элементами.
Схема реактора идеального вытеснения
В РИВ выполняются следующие допущения об идеальности:
1. Движущийся поток имеет плоский профиль линейных скоростей (то есть скорость движения потока в любой точке поперечного сечения реактора одинакова).
2. В любом сечении, перпендикулярном оси потока, все параметры выравнены.
3. Отсутствует перемешивание смеси в направлении оси потока.
Для реакторов непрерывного действия характерен стационарный режим работы, то есть параметры в реакторе не изменяются с течением времени.
Отсутствие перемешивания вдоль оси реактора идеального вытеснения при протекании в нем химической реакции приводит к неравномерному распределению концентраций участников реакции по длине аппарата.
Исходя из допущений об идеальности РИВ, за элементарный объем аппарата принимают бесконечно малый объем (dVp). В качестве элементарного объема можно рассматривать объем, вырезанный в канале двумя параллельными плоскостями, находящимися друг от друга на бесконечно малом расстоянии dl и перпендикулярными оси канала. По условию стационарности в качестве элементарного промежутка времени можно принять любой промежуток времени τ.
Изменение концентрации реагента А в реакторе идеального вытеснения по длине (объему) реактора и во времени в любой точке реактора
Следует отметить, что допущения об идеальности в реальных реакторах не выполняются. Из гидравлики известно, что даже очень гладкие каналы оказывают гидравлическое сопротивление движению потока. Наличие сопротивления движению приводит к уменьшению скорости движения потока от центра канала к стенкам.
|
|
Профили линейных скоростей потока при ламинарном, развитом турбулентном и идеальном режимах течения жидкости
Сравнивая профили скоростей при различных потоках, видим, что максимально приблизиться к идеальному вытеснению можно лишь в развитом турбулентном режиме. Однако турбулентный поток характеризуется наличием нерегулярных пульсаций, носящих хаотичный характер, в результате чего некоторые частицы потока могут опережать основной поток или отставать от него, т. е. произойдет частичное перемешивание в осевом направлении. Конечно, абсолютные значения таких перемещений будут невелики по сравнению с основным осевым перемещением потока и при больших линейных скоростях ими можно пренебречь. В то же время турбулентные пульсации в радиальном направлении будут способствовать локальному перемешиванию реагентов в сечении.
В реальном реакторе можно приблизиться к режиму идеального вытеснения, если:
1) реакционный поток — турбулентный;
2) длина канала существенно превышает его поперечный размер (например, для цилиндрических труб L/D > 20).
Материальный баланс РИВ
Материальный баланс показывает изменение количества реагента или продукта за счёт его поступления (со знаком плюс) и расходования (со знаком минус) в элементарном объёме за элементарный промежуток времени.
|
|
Запишем материальный баланс РИВ по взятому в недостатке реагенту A:
Здесь NAвх − количество (в молях) реагента A, поступающего со входящим в элементарный объём потоком реакционной массы за элементарный промежуток времени,
NAвых − количество (в молях) реагента A, уходящего с выходящим из элементарного объёма потоком реакционной массы за элементарный промежуток времени,
NAх.р − количество (в молях) реагента A, расходуемого на протекание химической реакции в элементарном объёме за элементарный промежуток времени.
Входящие в состав материального баланса РИС-Н слагаемые могут быть выражены через параметры процесса следующим образом:
(здесь CA − концентрация реагента A на входе в элементарный объём, Vo − объёмный расход реакционной смеси, τ − элементарный промежуток времени)
(здесь dCA − изменение концентрации реагента A в элементарном объёме, Vo − объёмный расход реакционной смеси, τ − элементарный промежуток времени)
(здесь WA − скорость химической реакции по компоненту A, dVр − элементарный объём, τ − элементарный промежуток времени)
При подстановке полученных выражений в уравнение материального баланса РИВ получим:
Преобразуем выражение, сократив на элементарный промежуток времени τ, и вынеся за скобку объёмный расход смеси Vo:
Отношение элементарного объёма dVр к объёмному расходу реакционной смеси Vo соответствует полному времени пребывания частиц в элементарном объёме (для сохранения аналогии с РИС-Н будем называть его средним временем пребывания):
Выразив среднее время пребывания частиц в элементарном объёме, получим дифференциальную форму характеристического уравнения РИВ:
|
|
Проинтегрировав 
на интервале от 0 до 
, рассчитаем среднее время пребывания частиц в РИВ:
Учитывая, что 
, получаем характеристическое уравнение РИВ:
Тепловой баланс РИВ
Тепловой баланс показывает изменение количества теплоты за счёт её поступления (со знаком плюс) и расходования (со знаком минус) в элементарном объёме за элементарный промежуток времени.
Запишем тепловой баланс политермического РИВ:
Здесь Qвх − количество теплоты, поступающей со входящим в элементарный объём потоком реакционной массы за элементарный промежуток времени,
Qвых − количество теплоты, уходящей с выходящим из элементарного объёма потоком реакционной массы за элементарный промежуток времени,
Qх.р − количество теплоты, выделяющейся (со знаком плюс) или поглощаемой (со знаком минус) при протекании химической реакции в элементарном объёме за элементарный промежуток времени,
Qт.о − количество теплоты, вносимой (со знаком плюс) в элементарный объём или отводимой (со знаком минус) из него за счёт теплообмена с теплоносителем или хладагентом за элементарный промежуток времени.
Входящие в состав теплового баланса РИВ слагаемые могут быть выражены через параметры процесса следующим образом:
(здесь ρo − плотность входящей в элементарный объём реакционной смеси, Vo − объёмный расход реакционной смеси, cpo − удельная теплоёмкость входящей в элементарный объём реакционной смеси, T − температура входящей в элементарный объём реакционной смеси, τ − элементарный промежуток времени),
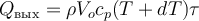
(здесь ρ − плотность выходящей из элементарного объёма реакционной смеси, Vo − объёмный расход реакционной смеси, cp − удельная теплоёмкость выходящей из элементарного объёма реакционной смеси, (T+dT) − температура выходящей из элементарного объёма реакционной смеси, τ − элементарный промежуток времени)
(здесь ΔH − тепловой эффект химической реакции, WA − скорость химической реакции по компоненту A, dVр − элементарный объём, τ − элементарный промежуток времени)
(здесь K т − коэффициент теплопередачи между теплоносителем или хладагентом и реакционной массой, dF − поверхность теплообмена между теплоносителем или хладагентом и элементарным объёмом, ΔT − положительная разность температур между теплоносителем или хладагентом и реакционной массой, τ − элементарный промежуток времени).
При подстановке полученных выражений в уравнение теплового баланса РИВ получим:
Преобразуем выражение, сократив на элементарный промежуток времени τ, и предполагая, что плотность и теплоёмкость реакционной смеси слабо зависят от температуры (ρocpo ≈ ρc p):
Выразим из материального баланса РИВ скорость реакции WA:
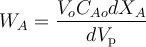
Подставим это выражение в тепловой баланс и разделим все слагаемые на CAoVo:
Учитывая, что мольная теплоёмкость с'p может быть рассчитана по формуле 
, получим конечное выражение теплового баланса для политермического РИВ:
В случае адиабатического теплового режима, характеризующегося отсутствием теплообмена реакционной смеси с теплоносителем или хладагентом (тепловая изоляция реактора), тепловой баланс РИВ примет вид:
=> вся теплота, выделяемая или поглощаемая в ходе химической реакции, идёт на изменение температуры реакционной смеси.
В случае изотермического теплового режима, характеризующегося постоянством температуры реакционной смеси, можно принять Qвх ≈ Qвых:
=> вся теплота, выделяемая или поглощаемая в ходе химической реакции, компенсируется теплообменом с хладагентом или теплоносителем.
Расчёт изотермического РИВ
Расчёт изотермического РИВ сводится к нахождению его объёма из уравнения материального баланса. Объём проточного реактора может быть рассчитан по уравнению:
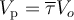
Среднее время пребывания частиц в реакторе рассчитывается по характеристическому уравнению РИВ:
Скорость реакции WA можно выразить через кинетическое уравнение:
(здесь k – константа скорости реакции, CA и CB – концентрации реагентов A и B, n и m – порядки реакции по компонентам A и B)
Для реакций, протекающих в газовой фазе с изменением объёма, текущая концентрация CA реагента A может быть рассчитана по уравнению:
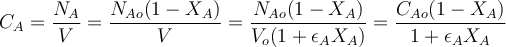
(здесь NA – количество (в молях) реагента A в объёме выходящего из реактора за единицу времени потока реакционной массы, NAo – количество (в молях) реагента A в объёме входящего в реактор за единицу времени потока реакционной массы, V – объёмный расход реакционной смеси на выходе из реактора, εA – коэффициент, учитывающий изменение объёма в ходе реакции)
Коэффициент, учитывающий изменение объёма в ходе реакции εA рассчитывается по формуле:
(здесь Δν – изменение количества моль газообразных реагентов в ходе реакции, nAo – объёмная доля реагента A в исходной смеси, a – стехиометрический коэффициент перед реагентом A в уравнении химической реакции)
При описании модельной газовой реакции вида 
изменение количества моль газообразных реагентов в ходе реакции Δν находят следующим образом:
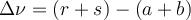
Для реакций, протекающих в жидкой фазе, или в газовой фазе без изменения объёма, текущая концентрация CA реагента A может быть рассчитана по уравнению: 
Для реакций, протекающих в газовой фазе с изменением объёма, текущая концентрация CB реагента B может быть рассчитана по уравнению:
(здесь NB – количество (в молях) реагента B в объёме выходящего из реактора за единицу времени потока реакционной массы, NBo – количество (в молях) реагента B в объёме входящего в реактор за единицу времени потока реакционной массы, V – объёмный расход реакционной смеси на выходе из реактора, a и b – стехиометрические коэффициенты перед реагентами A и B в уравнении химической реакции, εA – коэффициент, учитывающий изменение объёма в ходе реакции)
Для реакций, протекающих в жидкой фазе, или в газовой фазе без изменения объёма, текущая концентрация CB реагента B может быть рассчитана по уравнению: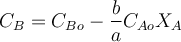 
После подстановки выражений для CA и CB в кинетическое уравнение получим:
Тогда среднее время пребывания частиц в реакторе рассчитывается по формуле:
Конечное выражение для расчёта объёма РИВ примет вид:
