Автокорреляция характерна в основном для временных рядов, поскольку они обладают естественной упорядоченностью, и сегодняшние значения переменных во многом обусловлены их прошлыми значениями, т.е.  является естественным следствием связи между значениями Yt и Yl+J. При анализе перекрестных выборок автокорреляция тоже встречается, но она бывает вызвана ошибками спецификации.
является естественным следствием связи между значениями Yt и Yl+J. При анализе перекрестных выборок автокорреляция тоже встречается, но она бывает вызвана ошибками спецификации.
Внешние признаки:
• очень высокие значения R2;
• высокие значения t-статистик;
• несущественные переменные кажутся значимыми.
Последствия автокорреляции:
• оценки МНК самих коэффициентов несмещены;
• оценки стандартных ошибок коэффициентов смещены;
• t-статистики неадекватны.
Критерий Бреуша-Годфри (Breusch-Godfrey). Этот критерий используется в ряде пакетов статистического анализа данных (например, в EVIEWS) для проверки гипотезы некоррелированности ошибок в модели наблюдений
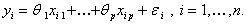
При наших предположениях это соответствует гипотезе независимости в совокупности случайных величин  Напомним, что критерий Дарбина — Уотсона основан на рассмотрении модели наблюдений, в которой случайные составляющие
Напомним, что критерий Дарбина — Уотсона основан на рассмотрении модели наблюдений, в которой случайные составляющие 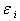 связаны соотношением
связаны соотношением

где 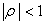 , а
, а 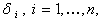 — независимые в совокупности случайные величины, имеющие одинаковое нормальное распределение
— независимые в совокупности случайные величины, имеющие одинаковое нормальное распределение 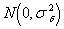 . В такой модели наблюдений случайные составляющие
. В такой модели наблюдений случайные составляющие 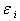 , разделенные двумя или более периодами времени и очищенные от влияния промежуточных
, разделенные двумя или более периодами времени и очищенные от влияния промежуточных 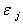 , оказываются независимыми.
, оказываются независимыми.
Критерий Бреуша-Годфри допускает зависимость случайных составляющих 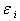 , разделенных
, разделенных 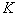 периодами времени и также очищенных от влияния промежуточных
периодами времени и также очищенных от влияния промежуточных 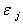 ; соответствующая модель зависимости имеет вид
; соответствующая модель зависимости имеет вид

Статистика этого критерия равна 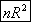 , где
, где  - коэффициент детерминации, получаемый при оценивании модели, а
- коэффициент детерминации, получаемый при оценивании модели, а 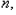 количество наблюдений в модели остатков. (то есть если проверяется автокорреляция 1-го порядка, то от первоначального числа наблюдений нужно отнять 1)
количество наблюдений в модели остатков. (то есть если проверяется автокорреляция 1-го порядка, то от первоначального числа наблюдений нужно отнять 1)
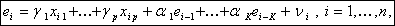
а 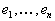
 - остатки, полученные при оценивании основной модели наблюдений. (Недостающие значения
- остатки, полученные при оценивании основной модели наблюдений. (Недостающие значения  заменяются нулями.)
заменяются нулями.)
В рамках последней модели проверяется гипотеза

Если эта гипотеза верна, то при большом количестве наблюдений 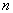 статистика критерия имеет распределение, близкое к распределению хи-квадрат с
статистика критерия имеет распределение, близкое к распределению хи-квадрат с 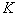 степенями свободы. Гипотеза
степенями свободы. Гипотеза 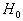 отвергается при заданном уровне значимости
отвергается при заданном уровне значимости 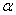 , если вычисленное значение
, если вычисленное значение 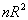 превышает критическое значение, равное квантили уровня
превышает критическое значение, равное квантили уровня  указанного распределения, т. е. если
указанного распределения, т. е. если
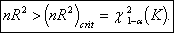
Конечно, при интерпретации результатов применения критерия Бреуша-Годфри следует помнить, что этот критерий асимптотический, тогда как критерий Дарбина-Уотсона точный. Однако возможность применения критерия Дарбина-Уотсона ограничивается тем, что он допускает зависимость «очищенных» случайных ошибок только на один шаг, т. е. 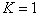 ;он неприменим в ситуациях, когда в число объясняющих переменных включаются запаздывающие значения объясняемой переменной. Критерий же Бреуша-Годфри свободен от этих ограничений.
;он неприменим в ситуациях, когда в число объясняющих переменных включаются запаздывающие значения объясняемой переменной. Критерий же Бреуша-Годфри свободен от этих ограничений.
Задание 1. По данным для 51 предприятия об объеме продаж товара (Sales- тысяч товара в месяц), средним ценам товара (Price – тысяч рублей) и среднесписочному количеству работников предприятий (Empl, тысяч человек), получены регрессионные модели соответственно:

1) Как можно интерпретировать полученные уравнения.
2) Оцените статистическое качество изучаемой зависимости на основе полученных моделей.
3) Найдите коэффициент эластичности продаж по цене в средней точке, если даны средние значения для экзогенных переменных 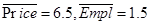
4) Найдите 99% доверительный интервал для коэффициента при переменной цены в модели, отражающей зависимость продаж от цен и трудовых ресурсов.
5) Проверти гипотезу о равенстве нулю суммы коэффициентов при экзогенных переменных исследуемой модели
Задание 2 Дано:  10
10
По экспериментальным данным построено уравнение регрессии: 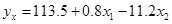
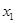
| ||||||||||
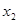
| ||||||||||
| у |
А) Проверьте гипотезу  Сделайте выводы.
Сделайте выводы.
Б) Определите наличие (отсутствие) автокорреляции с помощью метода рядов. Сделайте выводы.
Для справки:  =2,
=2,  =10.
=10.
Задание 3 (в Excel)
| Groups | Sales | Profits | R&D Expenditure | Groups | Sales | Profits | R&D Expenditure |
| 6375,3 | 185,1 | 62,5 | 80552,8 | 13869,9 | 6620,1 | ||
| 11626,4 | 1569,5 | 92,9 | 4487,8 | 3918,6 | |||
| 14655,1 | 276,8 | 178,3 | 10278,9 | 1595,3 | |||
| 21869,2 | 2828,1 | 258,4 | 8787,3 | 6107,5 | |||
| 26408,3 | 225,9 | 494,7 | 16438,8 | 4454,1 | |||
| 32405,6 | 3751,9 | 9761,4 | 3163,8 | ||||
| 35107,7 | 2884,1 | 1620,6 | 19774,5 | 13210,7 | |||
| 40295,4 | 4645,7 | 421,7 | 22626,6 | 1703,8 | |||
| 70761,6 | 5036,4 | 509,2 | 18415,4 | 9528,2 |