Лабораторная работа № 4
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Фильтром называется цепь, фильтрующая сигналы по частотам, т.е. пропускающая одни и не пропускающая другие частоты. Настоящая работа посвящена фильтрам верхних и нижних частот (ФВЧ и ФНЧ). Идеальные частотные характеристики таких фильтров изображены на рис. 1.
Реализовать такие характеристики в точности: с бесконечно крутым срезом, с постоянным коэффициентом передачи в области пропускания и нулевым вне её, конечно, невозможно. Степень приближения к ним зависит от типа фильтра.
Возможности фильтра определяются его порядком. Порядок фильтра – это порядок дифференциального уравнения, описывающего переходные процессы в соответствующей цепи.
Простейшие фильтры – это фильтры первого порядка – RC-цепочки. На рис. 2 изображены такие фильтры и их характеристики в логарифмическом масштабе. Наклон среза частотной характеристики составляет для них 20 дБ/дек и не может быть изменён. Для получения более крутого среза нужны фильтры более высоких порядков. Пассивный фильтр второго порядка содержит два реактивных элемента: индуктивность и ёмкость. В зависимости от того, с какого элемента снимается сигнал, получается ФВЧ и ФНЧ (рис.3). Частотные характеристики таких фильтров легко находятся методом комплексных амплитуд.
Для ФНЧ: 
или
. (1)
Для ФВЧ: 
или
. (2)
Форма характеристики, описываемая формулами (1 и 2), зависит от соотношения элементов, т.е. от добротности контура. При Q >>1 имеем узкий резонансный пик. При низких добротностях максимум слабый или совсем отсутствует, и резонанс только обеспечивает большую крутизну среза соответственно для ФВЧ и ФНЧ.
Уравнение переходных процессов для контура может быть написано по правилу Кирхгофа:
где R=R1+R2.
Дифференцируя и деля на L, получим:
Принимаем 
и 
Тогда уравнение переходных процессов имеет вид:
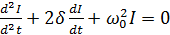. (3)
Соответствующее алгебраическое уравнение:
и 
.
Решение уравнения (З) имеет вид:
. (4)
Видно, что если 
(4а), то оба значения kдействительны отрицательны. Условие (4) можно переписать в виде:
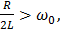то есть 
или 
Переходный процесс в этом случае описывается затухающей экспонентой, точно такой же, как для RC-цепи, т.е. при Q < 1/2 цепь второго порядка по своим свойствам не отличается от цепи первого порядка и её амплитудно-частотная характеристика имеет тот же срез 20 дБ/дек. Естественно, нет никакого смысла вводить в схему дополнительный элемент – индуктивность, если это не даёт никаких преимуществ. Поэтому такие добротности не применяются. В фильтрах второго порядка всегда Q > 1/2.
Чем больше Q, тем круче срез, но зато появляется и становится всё более заметным резонансный максимум. В зависимости от величины Q фильтры второго порядка носят разные названия: Фильтры Бесселя, Батерворта, Чебышева. Наибольшая крутизна среза, которую можно получить при плоской вершине без подъема на резонансной частоте, составляет 40 дБ/дек (в 2 раза больше, чем в RС-цепи). Обычно в фильтрах второго порядка используется добротность не выше 1,5, иначе резонансный максимум становится слишком резким.
Недостатком фильтров типа рис. 3 является наличие в них индуктивности. Катушка индуктивности является неудобным элементом схемы. Её параметры сильно зависят от температуры. Она вызывает заметные наводки в соседних элементах, воздействуя на них своим магнитным полем, и сама чувствительна к наводкам. Она громоздка, особенно на низких частотах, и не может быть выполнена в едином технологическом цикле с другими элементами интегральной схемы.
Другим недостатком пассивных фильтров является их сильная чувствительность к влиянию соединяемых с ними элементов: генератора и нагрузки, что приводит к необходимости применения буферных каскадов. По всем этим причинам в настоящее время пассивные фильтры в значительной степени вытеснены активными.
В активных фильтрах содержится один или несколько усилительных электронных приборов, чаще всего операционных усилителей.
Усилители охватываются обратными связями (ОС), содержащими конденсаторы, поэтому амплитуда и фаза подаваемых по ним сигналов зависят от частоты, активные фильтры не содержат катушек индуктивности, однако за счет ОС они могут представлять собой цепи второго и более высоких порядков.
ФВЧ и ФНЧ второго порядка выполняются чаще всего по схемам Саллена (рис.4).
Рассмотрим ФВЧ (рис.4б).
 |
ОУ с цепью ООС на делителе RЗ, R4 представляют собой неинвертирующий усилитель. Его усиление полностью определяется цепью ОС и равно:
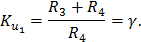
Коэффициент передачи цепи R2 С2 является комплексным и равен:
Если рассматривать усилитель совместно с этой цепью, то общий коэффициент усиления 
:
Цепь R1 С1 может рассматриваться как цепь ОС к этому усилителю. Тогда, согласно общему выражению для усилителя с ОС:
, (5)
где 
.
Подставляя выражения для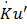 
и 
в (5), получим:
Производя умножение в знаменателе имеем:
.
Принимая R1С1 = R2С2 = 
, получим
или 
. (6)
Сопоставляя полученное выражение (6) с характеристикой пассивного фильтра второго порядка, можно видеть их аналогичность, т. е. с помощью фильтра Саллена и Кея можно реализовать совершенно такие же амплитудно-частотные характеристики, как и на основе пассивной цепи второго порядка. Роль сопротивления потерь (R1+R2) играет величина 
, которая может регулироваться выбором сопротивлений RЗ и R4.
Следует сразу отметить и отличие: сопротивление (R1+R2) может при большой добротности быть мало, но никогда не обращается в 0, величина же становится равной 0, если коэффициент усилителя 
. Количественно этот вывод неточен, так как при выводе (6) не учтено шунтирование цепи R1С1 цепью R2С2. Однако вывод полностью сохраняется: при уменьшении эквивалентного затухания (увеличении эквивалентной добротности) фильтра Саллена легко реализуется условие бесконечного коэффициента усиления, т.е. возникает генерация. Поэтому фильтры Саллена не используются для создания узкополосных фильтров с высокой эквивалентной добротностью. В ФВЧ и ФНЧ с добротностью Q<2 они далеки от возбуждения и достаточно удобны.
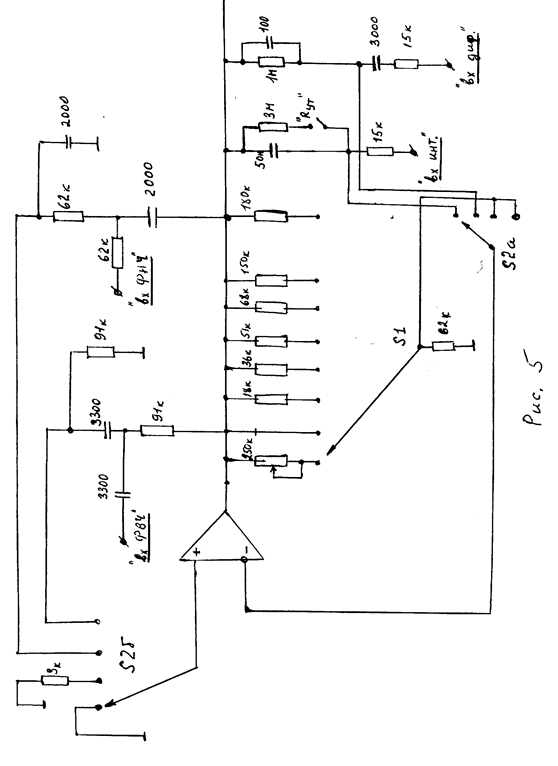
ОПИСАНИЕ МАКЕТА
Работа выполняется на том же макете, что и работа 3. Схема макета приведена на рис. 5. Делитель RЗR4 является общим для ФВЧ и ФНЧ. Переключение элементов этого делителя переключателем S1 позволяет изменять коэффициент усиления усилителя и эквивалентную добротность фильтра. Входные цепи ФВЧ и ФНЧ собраны независимо, и нужная цепь подключается переключателем S2. Входной сигнал подается на соответствующее гнездо "вх ФВЧ" или "вх ФНЧ".
ВЫПОЛНЕНИЕ РАБОТЫ
1. Исследование ФВЧ.
1) Снять АЧХ ФВЧ при различных элементах делителя (S1 в положениях 2-8). Отметить, в каких положениях наблюдается генерация, и оценить, каким коэффициентам усиления это соответствует. Для тех положений, где генерация отсутствует и фильтр работает устойчиво, снять по точкам AЧХ, построить все характеристики в логарифмическом масштабе.
2) Переключить S1 в положение 1, где ООС, а, значит, коэффициент усиления 
является регулируемым. Поставить схему на границу генерации. Убедиться, что фильтр превращается в резонансный. Снять и построить АЧХ в этом режиме.
2. Исследование ФНЧ производится аналогично ФВЧ. Снять и построить для этого фильтра АЧХ так же, как для ФВЧ.
Вопросы по теме "Активные фильтры верхних и нижних частот":
1) Что такое пассивные и активные фильтры?
2) Нарисовать характеристики идеальных фильтров верхних и нижних частот. Чем характеристики реальных фильтров отличаются от идеальных?
3) Какой вид имеет АЧХ фильтра нижних частот первого порядка? Как реализован такой фильтр на RC-элементах? Перейти к фильтру второго порядка так, чтобы характеристика фильтра стала ближе к идеальной. Изобразить, как изменится АЧХ.
4) Рассмотреть фильтр НЧ типа Саллена. Найти цепи положительной и отрицательной обратной связей. Какая из них является частотно зависимой?
5) Как влияет на АЧХ пассивного фильтра второго порядка увеличение добротности контура? Какие элементы и каким образом надо изменить в активном фильтре Саллена, чтобы получить аналогичные изменения АЧХ?
6) Ответить на вопросы, аналогичные 2-5, но по отношению к фильтру верхних частот.
7) Почему фильтр типа Саллена не используют для получения узкополосной резонансной характеристики фильтра?
