Система m линейных алгебраических уравнений с n неизвестными имеет вид:
 , (1)
, (1)
где числа а 11, а 12, …, аmn – коэффициенты системы;
числа b 1, b 2, …, bm – свободные члены;
х 1, х 2, …, хn – неизвестные.
Очевидно, не всякая система имеет решение, а если и имеет, то не обязательно одно.
Система уравнений называется совместной, если она имеет хотя бы одно решение. Если система уравнений решений не имеет, то она называется несовместной.
Для системы линейных алгебраических уравнений (СЛАУ) вида (1) имеют место три возможности:
 |
Решение системы (1) полностью определяется коэффициентами системы и свободными членами. Поэтому для исследования СЛАУ в высшей математике используют матричную форму записи.
Рассмотрим систему трех уравнений первой степени с тремя неизвестными x1, x2 и x3:
 (1)
(1)
Совокупность трехчисел называется решением системы (1), если после подстановки их вместо неизвестных во все уравнения системы каждое из этих уравнений превращается в тождество.
Пусть дана система вида (1), в которой число уравнений равно числу неизвестных. Обозначим через А матрицу системы, т.е.
 .
.
Для исследования вопроса о нахождении решения системы (1) с помощью формул Крамера необходимо предварительно вычислить следующие четыре определителя:
 ,
,  ,
,  ,
,  .
.
Определитель Δ называется определителем системы (1). Вспомогательные определители Δ1, Δ2, Δ3 получаются из определителя системы Δ заменой свободными членами элементов соответственно первого, второго и третьего столбцов.
При решении системы (1) возможны три различные ситуации.
1. Если определитель Δ системы (1) отличен от нуля (Δ ≠ 0), то существует единственное решение этой системы, которое находится по формулам Крамера:
 ,
,  ,
,  .
.
2. Если определитель системы равен нулю (Δ = 0) и хотя бы один из определителей Δ1, Δ2, Δ3 отличен от нуля, то система (1) решений не имеет, т.е. несовместна.
3. В случае равенства нулю всех определителей (Δ=Δ1 =Δ2 =Δ3 = 0) система (1) либо совсем не имеет решений, либо имеет бесконечно много решений (если есть хотя бы одно).
Пример 1.1. Найти решение системы:
 .
.
Решение. Составим и вычислим определитель системы D:
 ;
;
 , следовательно, существует единственное решение.
, следовательно, существует единственное решение.
Вспомогательные определители равны:
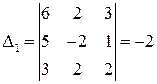 ;
;  ;
; 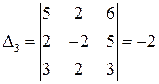 .
.
В соответствии с формулами Крамера, найдем неизвестные системы:
 ;
;  ;
;  .
.
Проверка. Подставим полученные значения неизвестных в систему:
 ,
,  .
.
Все уравнения системы обратились в тождества, следовательно, найденные значения неизвестных являются ее решением.
Ответ: (1; –1; 1).
Пример 1.2. Решить систему с помощью формул Крамера:
 .
.
Решение. Составим и вычислим определитель системы и вспомогательные определители:
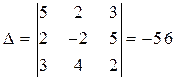 ;
; 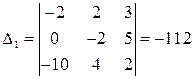 ;
;
 ;
;  .
.
Применив формулы Крамера, получим:
 ;
;  ;
;  .
.
Проверка. Подставим полученные значения неизвестных в систему:
 .
.
Ответ: (2, –3, –2).
Пример 1.3. Решить систему:
 .
.
Решение. Основной определитель системы

(по свойству определителей, если определитель имеет два одинаковых столбца, то он равен нулю).
Вычисляем вспомогательные определители:
 (по тому же свойству);
(по тому же свойству);
 ,
,
Получили вспомогательный определитель, отличный от нуля, следовательно, данная система не имеет решения.
Ответ: система несовместна.
Пример 1.4. Найти решения системы
 .
.
Решение. Вычисляем определители, используя свойство о равенстве столбцов:
 ,
,  ,
,  ,
,  .
.
Все четыре определителя равны нулю, значит, система либо совсем не имеет решений, либо их бесконечно много.
Анализируя данную систему, убеждаемся, что первое и второе уравнения противоречивы: умножая первое уравнение на 2 и вычитая из второго, получим невозможное равенство 0 = 1.
Таким образом, система не имеет решения.
Ответ:система несовместна.
Пример 1.5. Решить систему с помощью формул Крамера (определители вычислить разложением по строке или столбцу):
 .
.
Решение. Вычислим основной определитель системы разложением по 1-й строке:

 .
.
Вспомогательные определители:
 ;
;
 ;
;
 .
.
Применив формулы Крамера, получим решение системы:
 ;
;  ;
;  .
.
Проверка:
 .
.
Ответ: (1, 1, 1).
Пример 1.6. Решить систему с помощью формул Крамера:
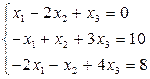 .
.
Решение. Составим и вычислим определитель системы и вспомогательные определители:
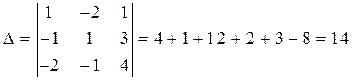 ;
;
вспомогательные определители вычислим разложением по 1-й строке:
 ;
;
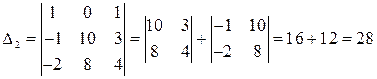 ;
;
 .
.
По формулам Крамера получаем:
 ;
;  ;
;  .
.
Проверка. Подставим полученные значения неизвестных в систему:
 .
.
Ответ: (1, 2, 3).
Пример 1.7. Решить систему с помощью формул Крамера:
 .
.
Решение. Составим и вычислим определитель системы и вспомогательные определители:
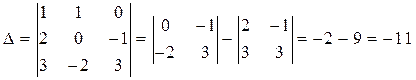 ;
;
вспомогательные определители вычислим разложением по 1-й строке:
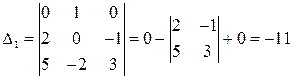 ;
;
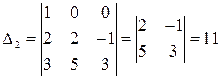 ;
;
 .
.
Тогда решение системы:
 ;
;  ;
; 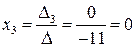 .
.
Проверка.
 .
.
Ответ: (1, –1, 0).
Пример 1.8. Решить систему с помощью формул Крамера:
 .
.
Решение.
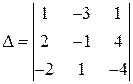
Определитель системы  , так как 2-я и 3-я строки пропорциональны.
, так как 2-я и 3-я строки пропорциональны.
 .
.
Определитель  , следовательно, система не имеет решения.
, следовательно, система не имеет решения.
Ответ: система несовместна.
Пример 1.9. Решить систему с помощью формул Крамера:
 .
.
Решение. Составим и вычислим определитель системы и вспомогательные определители:
 ;
;  ;
;
 ;
; 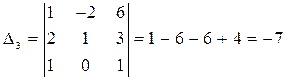 .
.
Применив формулы Крамера, получим:
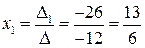 ;
;  ;
;  .
.
Проверка. Подставим полученные значения неизвестных в систему:
 ;
; 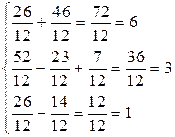 .
.
Ответ:  .
.
Пример 1.10. Решить систему с помощью формул Крамера:
 .
.
Решение. Вычислим определители:
 ;
;  ;
;  ;
;
 .
.
Решение системы получаем по формулам Крамера:
 ;
;  ;
;  .
.
Проверка. Подставим полученные значения неизвестных в систему:

Ответ:  .
.
Примеры для самостоятельного решения (под контролем преподавателя):
1.11.  1.12.
1.12. 
1.13.  1.14.
1.14. 
Ответы:
1.11.  .
.
1.12. 
1.13. Система несовместна.
1.14.  .
.