Электрический расчет линии электропередач позволяет подсчитать потери мощности и напряжения на всем протяжении линии. Исходя из результатов электрического расчета, можно судить о качестве подаваемой потребителю электрической энергии.
В электрическом расчете учитываются активная и реактивная составляющие мощности, передаваемой по линии. Реактивная составляющая мощности в свою очередь делится на индуктивную и емкостную. Оба этих слагаемых реактивной составляющей мощности зависят от среднегеометрического расстояния между проводами, т.е. от положения проводников в пространстве.
В таблице 3 приведены данные для электрического расчета линии.
Таблица 3. Исходные данные для электрического расчета ЛЭП
| Длина линии (L), км | |
Номинальное напряжение (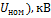
| |
| Марка провода | АС – 35/6.2 |
Удельное активное сопротивление (
| 0.84 |
Удельное индуктивное сопротивление ( , Ом/км
| 0.403 |
Удельная емкостная проводимость ( , См/км
| 
|
Определим активную и реактивную составляющие выработанной мощности:
;
;
.
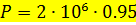Произведем расчет сопротивлений линии, используя формулы:
где 
– удельное активное сопротивление провода марки АС – 35/6.2;
– индуктивное сопротивление провода марки АС – 35/6.2;
– емкостная проводимость провода марки АС – 35/6.2;
l – длина линии.
Подставляя в формулы (7), (8), (9) значения из таблицы 4 получаем следующие значения:
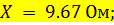
Для определения величин продольного и поперечного падений напряжений в линии используют следующие формулы:
где Р – активная мощность в начале линии;
Q – реактивная мощность в начале линии;
R и X – активная и индуктивная составляющие сопротивления линии;
|
|
U – рабочее напряжение линии.
Подставив в формулы (10) и (11) значения мощностей, сопротивлений и напряжения, получаем следующие значения падения напряжения в ЛЭП (продольной и поперечной составляющей соответственно):
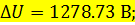
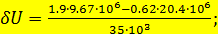
Продольная и поперечная составляющие падения напряжения складываются векторно и для получения значения падения рабочего напряжения используют выражение:
Подставим в формулу (12), значения падения напряжений, получим значение падения рабочего напряжения для данной линии:
Падение напряжения в линии составляет 3.7 %, что соответствует требованиям ПУЭ к качеству электрической энергии, подаваемой потребителю.
Произведем расчет потерь мощности в данной ЛЭП, используя формулы:
Выражения (13) и (14) отражают потери активной и реактивной мощностей в данной ЛЭП соответственно. Подставим значения вырабатываемых мощностей и сопротивлений в формулы и произведем расчет:
Рассчитаем величину индуктивных потерь мощности по линии по формуле:
Общие потери реактивной мощности рассчитываются по формуле:
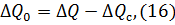
Тогда для линии получаем следующую величину потерь реактивной мощности:
Векторно сложив активную и реактивную составляющие потерь мощности, получим величину потерь полной мощности:
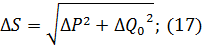
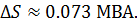
Рассчитаем полную мощность на конце ЛЭП:
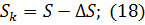
Определим КПД ЛЭП и сведем в таблицу данные о потерях в линии, чтобы сделать заключение о качестве подаваемой потребителю посредством данной ЛЭП электрической энергии.
Для определения КПД используется формула:
|
|
Таблица 4. Результаты электрического расчета ЛЭП
| Активная мощность вначале линии (Р), МВт | 1.9 |
Активная мощность в конце линии ( ), МВт
| 1.83 |
Потери активной мощности на линии ( МВт
| 0.067 |
Потери реактивной мощности в линии ( , МВар
| 0.032 |
Потери полной мощности на линии (
| 0.073 (3.7 %) |
Продольная составляющая падения напряжения в линии (
| 1278.73 |
Поперечная составляющая падения напряжения в линии (
| 163.57 |
Падение рабочего напряжения линии (
| 1289.15 (3.7 %) |
КПД ЛЭП, 
| 96.5 % |
По результатам электрического расчета можно сделать вывод о том, что качество электрической энергии, подаваемое посредством ЛЭП потребителю, удовлетворяет требованиям ПУЭ: потери напряжения не превышают 10 % от номинального значения, что соответствует максимально возможному значению регулирования трансформатора.
Потери полной мощности также не превышают 10 % от номинальной величины. ЛЭП имеет КПД, равный 96.5 %.