Теорема Безу
Теорема. Остаток от деления многочлена  на многочлен
на многочлен  равен
равен 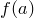 .
.
Доказательство. Степень остатка меньше 1, следовательно, остаток — константа. Пусть  — остаток.
— остаток.

Это равенство верно при любых значениях  . Положим
. Положим  :
:

Пусть  - корень многочлена
- корень многочлена  , тогда, по теореме Безу,
, тогда, по теореме Безу, 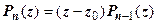 . Возможны два варианта: 1. Число
. Возможны два варианта: 1. Число  не является корнем многочлена
не является корнем многочлена  , в этом случае
, в этом случае  называется простым корнем многочлена
называется простым корнем многочлена  .
.
2. Число  является корнем многочлена
является корнем многочлена  , тогда, применяя теорему Безу уже к
, тогда, применяя теорему Безу уже к  , получим
, получим 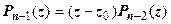 ,
,  . Применяя к
. Применяя к 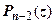 те же рассуждения, придём к выводу: если
те же рассуждения, придём к выводу: если  - корень многочлена
- корень многочлена  , то
, то  единственным образом представляется в виде
единственным образом представляется в виде 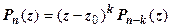 , где
, где  . Число
. Число  в этом случае называется кратностью корня
в этом случае называется кратностью корня  .
.
Согласно основной теореме алгебры, любой многочлен  при
при  имеет хотя бы один корень
имеет хотя бы один корень  ; если кратность этого корня равна
; если кратность этого корня равна  , то, согласно изложенному,
, то, согласно изложенному,  представляется в виде
представляется в виде  , где
, где  . Если
. Если 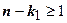 , то многочлен
, то многочлен 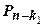 имеет корень
имеет корень 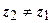 , и представляется в виде
, и представляется в виде  . Если
. Если 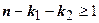 , эти выкладки можно продолжить; окончательный вывод формулируется так: любой многочлен
, эти выкладки можно продолжить; окончательный вывод формулируется так: любой многочлен  степени
степени 
при старшем коэффициенте 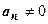 единственным (с точностью до порядков сомножителей) образом может быть представлен в виде
единственным (с точностью до порядков сомножителей) образом может быть представлен в виде 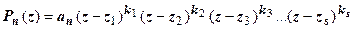 , где
, где  - (попарно различные) корни многочлена,
- (попарно различные) корни многочлена, 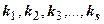 - их кратности,
- их кратности, 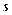 - количество различных корней. Общее число корней многочлена с учётом их кратностей равна
- количество различных корней. Общее число корней многочлена с учётом их кратностей равна 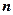 :
:  .
.
34. Многочлены с действительными коэффициентами. В этом разделе мы рассмотрим многочлен  от комплексной переменной
от комплексной переменной 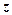 , в предположении, что его коэффициенты
, в предположении, что его коэффициенты 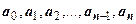 - действительные числа. Сформулируем и докажем ряд свойств такого многочлена.
- действительные числа. Сформулируем и докажем ряд свойств такого многочлена.
1.Если  - число, сопряжённое к числу
- число, сопряжённое к числу 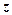 , то
, то  . Док-во: Для любого действительного числа
. Док-во: Для любого действительного числа  операция сопряжения не меняет это число:
операция сопряжения не меняет это число:  , поэтому
, поэтому
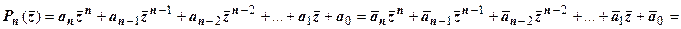

2. Если 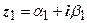 - корень многочлена
- корень многочлена  , то
, то 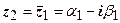 - тоже корень этого многочлена. Док-во: если
- тоже корень этого многочлена. Док-во: если  , то
, то  .
.
3. Если 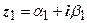 - корень многочлена с действительными коэффициентами
- корень многочлена с действительными коэффициентами  , то
, то  без остатка делится на квадратный трёхчлен
без остатка делится на квадратный трёхчлен  , где
, где  . Док-во: так как числа
. Док-во: так как числа 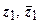 - корни
- корни  , то
, то  представляется в виде
представляется в виде 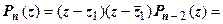
 .
.
4. Если 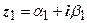 - корень многочлена
- корень многочлена  кратности
кратности  , то
, то 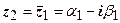 - корень этого многочлена той же кратности. Док-во: непосредственно следует из утверждений 2,3.
- корень этого многочлена той же кратности. Док-во: непосредственно следует из утверждений 2,3.
5. Любой многочлен 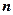 -ой степени
-ой степени  может быть представлен, и притом единственным с точностью до порядка сомножителей образом, в виде
может быть представлен, и притом единственным с точностью до порядка сомножителей образом, в виде
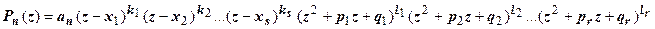 , где
, где
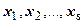 - попарно различные действительные корни этого многочлена,
- попарно различные действительные корни этого многочлена,  - их кратности, квадратные трёхчлены (соответствующие попарно различным парам сопряжённых корней
- их кратности, квадратные трёхчлены (соответствующие попарно различным парам сопряжённых корней 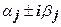 кратностей
кратностей  )
)  с действительными коэффициентами не имеют действительных корней (т.е.
с действительными коэффициентами не имеют действительных корней (т.е.  ),
),  . Это утверждение непосредственно следует из результатов этого и предыдущего разделов.
. Это утверждение непосредственно следует из результатов этого и предыдущего разделов.
6. При выводе предыдущего утверждения мы существенно использовали тот факт, что 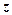 - комплексная переменная (в частности, когда ссылались на основную теорему алгебры). В то же время в самом полученном представлении многочлена все участвующие величины (кроме
- комплексная переменная (в частности, когда ссылались на основную теорему алгебры). В то же время в самом полученном представлении многочлена все участвующие величины (кроме 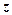 ) - действительные числа. Предположим теперь, чтобы переменная
) - действительные числа. Предположим теперь, чтобы переменная 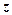 принимает только действительные значения, т.е.
принимает только действительные значения, т.е. 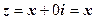 . Тогда утверждение 5 можно переформулировать так: любой многочлен с действительными коэффициентами
. Тогда утверждение 5 можно переформулировать так: любой многочлен с действительными коэффициентами  от действительной переменной
от действительной переменной 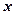 может быть представлен, и притом единственным с точностью до порядка сомножителей образом, в виде
может быть представлен, и притом единственным с точностью до порядка сомножителей образом, в виде
 , где смысл всех параметров описан выше.
, где смысл всех параметров описан выше.
Определение. Пусть  и
и  — многочлены,
— многочлены, 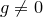 . Будем говорить, что
. Будем говорить, что  поделен на
поделен на  с остатком, если
с остатком, если  представлен в виде
представлен в виде 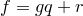 , где
, где 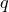 и
и  — многочлены, причем
— многочлены, причем 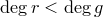 .
.
Полином  называется остатком от деления
называется остатком от деления  на
на  ,
, 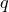 — неполным частным.
— неполным частным.
Пример. 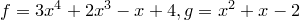 .
.
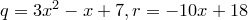 .
.
Теорема. (о делении с остатком). Пусть  и
и  — полиномы над полем
— полиномы над полем  ,
, 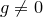 . Тогда существуют единственные многочлены
. Тогда существуют единственные многочлены 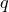 и
и  над полем
над полем  такие, что
такие, что 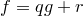 и
и 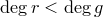 .
.
Доказательство. Существование.
Пусть  . Положим
. Положим  .
.
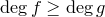 .
.
Предположим, что теорема верна не для любого полинома  (
( фиксируем). Среди всех многочленов
фиксируем). Среди всех многочленов  , для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его
, для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его  :
:
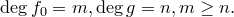
Пусть  . Положим
. Положим
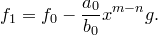
Коэффициент при 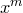 в многочлене
в многочлене  равен
равен  . Следовательно,
. Следовательно, 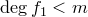 . Значит, для многочлена
. Значит, для многочлена  теорема верна. Существуют такие
теорема верна. Существуют такие 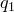 и
и  , что
, что 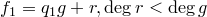 . Тогда
. Тогда
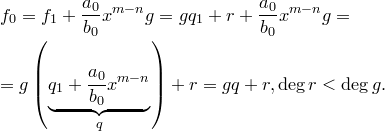
Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.
Единственность. Предположим, что

1)  . Значит,
. Значит,  ,
,
2)  .
.

Получили противоречие. Этот случай невозможен.
35. Теорема о целых корнях, заключающая в себе
Если целое число α - корень многочлена с целыми коэффициентами, то α - делитель его свободного члена.
Доказательство. Пусть:
P (x)=a0xⁿ +a1xⁿ-1+…+an-1x +an
многочлен с целыми коэффициентами и целое число α −его корень.
Тогда по определению корня выполняется равенство P (α)=0;
a0 αⁿ+a1 αⁿ-1+…+an-1 α +an=0.
Вынося общий множитель α за скобки, получим равенство:
α(a0 αⁿ-1 +a1 αⁿ-2 +…+an-1)+an=0, откуда
an= -α(a0 αⁿ-1 +a1 αⁿ-2 +…+an-1)
Так как числа a0, a1,…an-1, an и α −целые, то в скобке стоит целое число, и, следовательно, an делится, на α, что и требовалось доказать.
Доказанная теорема может быть сформулирована и следующим образом: всякий целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
На теореме основан алгоритм поиска целых корней многочлена с целыми коэффициентами: выписать все делители свободного члена и поочерёдно выписать значения многочленов этих чисел.
2.Дополнительная теорема о целых корнях
Если целое число α−корень многочлена P(x) с целыми коэффициентами, то α-1−делитель числа P(1), α+1−делитель числа P(-1)
Доказательство. Из тождества
xⁿ-yⁿ=(x-y)(xⁿ-1+xⁿ-2y+…+ xyⁿ-2+yⁿ-1)
вытекает, что для целых чисел b и c число bⁿ-cⁿ делится на b∙c. Но для любого многочлена P разность
P (b)-P(c)= (a0bⁿ+a1bⁿ-1+…+an-1b+an)-(a0cⁿ+a1cⁿ-1+…+an-1c+an)=
=a0(bⁿ- cⁿ)+a1(bⁿ-1-cⁿ-1)+…+an-1(b-c)
и, следовательно, для многочлена P с целыми коэффициентами и целых чисел b и c разность P(b)-P(c) делится на b-c.
Затем: при b = α, с=1, P (α)-P (1)= -P(1), а значит, P(1) делится на α-1. Аналогично рассматривается второй случай.
Теорема о рациональных корнях многочлена
Если многочлен

|
с целыми коэффициентами имеет рациональный корень  то число p является делителем числа
то число p является делителем числа  (свободного члена), а число q является делителем числа
(свободного члена), а число q является делителем числа 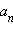 (старшего коэффициента).
(старшего коэффициента).
Доказательство
Пусть все коэффициенты многочлена 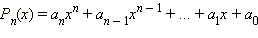 являются целыми числами, и пусть целое число a является корнем этого многочлена. Так как в этом случае
являются целыми числами, и пусть целое число a является корнем этого многочлена. Так как в этом случае  то отсюда следует, что коэффициент
то отсюда следует, что коэффициент  делится на a.
делится на a.
Замечание. Эта теорема фактически позволяет находить корни многочленов высших степеней в том случае, когда коэффициенты этих многочленов − целые числа, а корень − рациональное число. Теорему можно переформулировать так: если нам известно, что коэффициенты многочлена − целые числа, а корни его − рациональны, то эти рациональные корни могут быть только вида  где p является делителем числа
где p является делителем числа  (свободного члена), а число q является делителем числа
(свободного члена), а число q является делителем числа 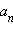 (старшего коэффициента).
(старшего коэффициента).
Схема Горнера
Теорема: Пусть несократимая дробь p/q является корнем уравнения a0xn+a1xn−1+ 

 +an−1x+an =0 c целыми коэффициентами, тогда число q является делителем старшего коэффициента a0, а число р является делителем свободного члена an.
+an−1x+an =0 c целыми коэффициентами, тогда число q является делителем старшего коэффициента a0, а число р является делителем свободного члена an.
Замечание 1. Любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена.
Замечание 2. Если старший коэффициент уравнения с целыми коэффициентами равен 1, то все рациональные корни, если они существуют - целые.
Корень многочлена. Корнем многочлена f(x)= a0xn+a1xn−1+ 

 +an−1x+an является x = c, такое, что f(c)=0.
+an−1x+an является x = c, такое, что f(c)=0.
Замечание 3. Если x = c корень многочлена f(x)=a0xn+a1xn−1+ 

 +an−1x+an, то многочлен можно записать в виде: f(x)=(x−c)q(x), где q(x)=b0xn−1+b1xn−2+
+an−1x+an, то многочлен можно записать в виде: f(x)=(x−c)q(x), где q(x)=b0xn−1+b1xn−2+ 

 +bn−2x+bn−1 это частное от деления многочлена f(x) на одночлен x - c
+bn−2x+bn−1 это частное от деления многочлена f(x) на одночлен x - c
Деление многочлена на одночлен можно выполнить по схеме Горнера:
Если f(x)=a0xn+a1xn−1+ 

 +an−1x+an, a0≠0, g(x)=x−c, то при делении f(x) на g(x) частное q(x) имеет вид q(x)=b0xn−1+b1xn−2+
+an−1x+an, a0≠0, g(x)=x−c, то при делении f(x) на g(x) частное q(x) имеет вид q(x)=b0xn−1+b1xn−2+ 

 +bn−2x+bn−1, где b0=a0,
+bn−2x+bn−1, где b0=a0,
bk=c  bk−1+ak, k=1, 2,
bk−1+ak, k=1, 2, 

 ,n−1. Остаток r находится по формуле r=c
,n−1. Остаток r находится по формуле r=c  bn−1+an
bn−1+an
| a0 | a1 | a2 | ... | an−1 | an | |
| x = c | b0=a0 | b1=c  b0+a1 b0+a1
| b2=c  b1+a2 b1+a2
| ... | bn−1=c  bn−2+an−1 bn−2+an−1
| r=c  bn−1+an bn−1+an
|
В первой строке этой таблицы записывают коэффициенты многочлена f(х). Если какая-то степень переменной отсутствует, то в соответствующей клетке таблицы пишется 0. Всегда старший коэффициент частного равен старшему коэффициенту делимого b0=a0. Если x = c является корнем многочлена, то в последней клетке получается 0, т.е. остаток от деления будет равен нулю.
Пример. Решить уравнение x3−x2−8x+12=0
| a0=1 | a1=−1 | a2=−8 | a3=12 | ||
| x = 1 | -8 | не корень | |||
| x = -1 | -2 | -6 | не корень | ||
| x = 2 | -6 | корень |
Решение: Коэффициент при старшей степени равен 1, поэтому целые корни уравнения надо искать среди делителей свободного члена: 1; 2; 3; 4; 6; 12. используя схему Горнера, найдем целые корни уравнения:
Если один корень подобран по схеме Горнера. то можно дальше решать так x3−x2−8x+12=(x−2)(x2+x−6)=0  (x−2)2(x−3)=0
(x−2)2(x−3)=0  x=2;x=3
x=2;x=3
Формула Кардано
Формула Кардано — формула для нахождения корней канонической формы кубического уравнения

над полем комплексных чисел. Названа в честь итальянского математика Джероламо Кардано.
Любое кубическое уравнение общего вида

при помощи замены переменной
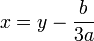
может быть приведено к указанной выше канонической форме с коэффициентами
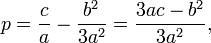

Формула
Определим Q:

Если все коэффициенты кубического уравнения вещественны, то и Q вещественно, и по его знаку можно определить тип корней:
Дискриминант многочлена 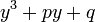 при этом равен
при этом равен 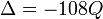 .
.
- D > 0 — три вещественных корня.
- D = 0 — один однократный вещественный корень и один двукратный, или, если p = q = 0, то один трёхкратный вещественный корень.
- D < 0 — один вещественный корень и два сопряженных комплексных корня. Это так называемый «неприводимый» случай, и именно при анализе этой ситуации впервые исторически возникло понятие комплексного числа.
По формуле Кардано, корни кубического уравнения в канонической форме равны:
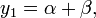
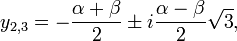
где
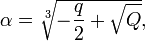
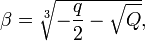
Применяя данные формулы, для каждого из трёх значений  необходимо брать такое
необходимо брать такое  , для которого выполняется условие
, для которого выполняется условие 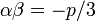 (такое значение
(такое значение  всегда существует).
всегда существует).
Если кубическое уравнение вещественное, то рекомендуется по возможности выбирать вещественные значения  .
.