
 (1)
(1)
 - допустимое множество задачи математического программирования,
- допустимое множество задачи математического программирования,
 .
.
 - функция Лагранжа задачи (1), где
- функция Лагранжа задачи (1), где 

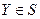 .
.
 - градиент функции Лагранжа по координатам вектора
- градиент функции Лагранжа по координатам вектора  , то есть вектор, составленный из частных производных функции Лагранжа по координатам вектора
, то есть вектор, составленный из частных производных функции Лагранжа по координатам вектора  :
:
 .
.
 - матрица вторых частных производных функции Лагранжа по координатам вектора
- матрица вторых частных производных функции Лагранжа по координатам вектора  .
.
Сформулируем известный из курса математического анализа результат о существовании решения задачи (1):
Теорема 1 (Теорема Вейерштрасса)
Пусть  - компакт (ограниченное и замкнутое множество) в
- компакт (ограниченное и замкнутое множество) в  ,
, 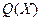 - непрерывная функция на
- непрерывная функция на  . Тогда точка глобального минимума функции
. Тогда точка глобального минимума функции 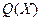 на
на  (глобальное решение задачи (1)) существует.
(глобальное решение задачи (1)) существует.
1. Пусть  - замкнутое множество на
- замкнутое множество на  ,
, 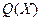 - непрерывная функция на
- непрерывная функция на  , причём при некотором
, причём при некотором  множество
множество  ограничено. Доказать, что тогда точка глобального минимума функции
ограничено. Доказать, что тогда точка глобального минимума функции 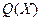 на
на  существует.
существует.
2. Известно, что функция 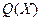 непрерывна на
непрерывна на  и удовлетворяет следующему условию:
и удовлетворяет следующему условию: 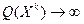 для любой последовательности
для любой последовательности 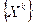 такой, что
такой, что 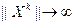 ,
,  . Доказать, что тогда функция
. Доказать, что тогда функция 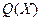 достигает своего минимального значения на любом замкнутом множестве из
достигает своего минимального значения на любом замкнутом множестве из  .
.
3. Пусть непрерывная функция 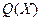 имеет точку глобального минимума на
имеет точку глобального минимума на  . Следует ли отсюда, что функция
. Следует ли отсюда, что функция 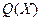 имеет точку глобального минимума на любом замкнутом множестве из
имеет точку глобального минимума на любом замкнутом множестве из  ?
?
4. Пусть  - точка строгого локального минимума функции
- точка строгого локального минимума функции  на
на  (
( ). Можно ли утверждать, что
). Можно ли утверждать, что  убывает в некоторой левой полуокрестности точки
убывает в некоторой левой полуокрестности точки  и возрастает в некоторой правой полуокрестности
и возрастает в некоторой правой полуокрестности  ?
?
5. Убедиться, что функция  достигает локального минимума в точке
достигает локального минимума в точке 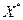 = (0,0) вдоль каждой прямой, проходящей через
= (0,0) вдоль каждой прямой, проходящей через 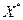 , но
, но 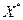 не является точкой локального минимума этой функции.
не является точкой локального минимума этой функции.
Задача математического программирования (1) называется задачей безусловной оптимизации, если 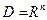 , то есть
, то есть
 (2)
(2)
Теорема 2 (Необходимое условие локальной оптимальности первого порядка)
Пусть функция 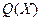 дифференцируема в точке
дифференцируема в точке  . Если
. Если 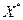 - локальное решение задачи (2), то
- локальное решение задачи (2), то
 . (3)
. (3)
Теорема 3 (Необходимое условие локальной оптимальности второго порядка)
Пусть функция 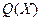 дважды дифференцируема в точке
дважды дифференцируема в точке  . Если
. Если 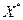 - локальное решение задачи (2), то матрица
- локальное решение задачи (2), то матрица  - неотрицательно определена, то есть
- неотрицательно определена, то есть
 при всех
при всех  . (4)
. (4)
Теорема 4 (Достаточное условие локальной оптимальности)
Пусть функция 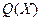 дважды дифференцируема в точке
дважды дифференцируема в точке  и
и  , а матрица
, а матрица  положительно определена, то есть
положительно определена, то есть
 при всех
при всех  ,
, 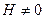 . (5)
. (5)
Тогда 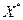 - строгое локальное решение задачи (2).
- строгое локальное решение задачи (2).
Теорема 5 (Критерий Сильвестра)
Симметрическая матрица является неотрицательно (положительно) определенной, тогда и только тогда, когда все её главные (угловые) миноры неотрицательны (положительны).
Пример 1.
Рассмотрим задачу безусловной оптимизации:
 .
.
Решение:
- Выпишем необходимое условие локальной оптимальности первого порядка:

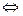
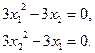
Решениями этой системы являются точки  = (0,0),
= (0,0), 
- Рассмотрим гессиан функции
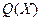 в точках
в точках  и
и  :
:
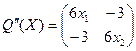
 ,
,  .
.
Матрица  по критерию Сильвестра не является неотрицательно определённой, то есть необходимое условие локальной оптимальности второго порядка не выполняется. Отсюда следует, что точка
по критерию Сильвестра не является неотрицательно определённой, то есть необходимое условие локальной оптимальности второго порядка не выполняется. Отсюда следует, что точка  = (0,0) не может быть решением задачи.
= (0,0) не может быть решением задачи.
Матрица  положительно определена. Следовательно, выполняется достаточное условие локальной оптимальности. Точка
положительно определена. Следовательно, выполняется достаточное условие локальной оптимальности. Точка  – строгое локальное решение задачи.
– строгое локальное решение задачи.
В следующих задачах требуется привести примеры функций одной или двух переменных, в которых выполняются указанные ниже требования.
6. Глобальные максимум и минимум достигаются в бесконечном числе точек.
7. Функция ограничена, глобальный максимум достигается, а глобальный минимум не достигается.
8. Функция ограничена, но глобальные минимум и максимум не достигаются.
9. Функция ограничена, имеет локальные минимумы и максимумы, но глобальные максимум и минимум не достигается.
10. Имеется единственный локальный экстремум, не являющийся глобальным.
11. Имеется бесконечное число локальных минимумов, но нет ни одного локального максимума.
12. Найти все точки локального минимума и локального максимума функции  на
на  .
.
Найти локальные решения в задачах 13-16.
13. 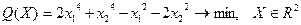 .
.
14. 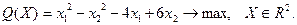
15. 
16. 
17. Найти наименьшее значение функции  , где
, где  ;
;  - заданные числа.
- заданные числа.
18. Показать, что в методе наискорейшего спуска направления  и
и 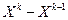 - ортогональны.
- ортогональны.
Напомним, что метод наискорейшего спуска предназначен для отыскания локального минимума функции  и задаётся расчётной формулой
и задаётся расчётной формулой  для заданной точки
для заданной точки  и
и  , которые выбираются из условия минимизации функции вдоль направления антиградиента для каждого
, которые выбираются из условия минимизации функции вдоль направления антиградиента для каждого  .
.
Задача математического программирования (1) называется классической задачей на условный экстремум, если 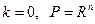 , то есть
, то есть
 (6)
(6)
Функция Лагранжа классической задачи на условный экстремум определена при  ,
,  ,
,  .
.
Теорема 6 (Необходимое условие локальной оптимальности первого порядка)
Пусть функции  непрерывно дифференцируемы в некоторой окрестности точки
непрерывно дифференцируемы в некоторой окрестности точки  . Если
. Если 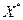 - локальное решение задачи (6), то существует число
- локальное решение задачи (6), то существует число 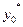 и вектор
и вектор  не равные нулю одновременно и такие, что
не равные нулю одновременно и такие, что
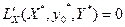 . (7)
. (7)
Если градиенты 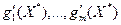 линейно независимы, то
линейно независимы, то  .
.
Условие линейной независимости градиентов ограничений в точке 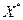 называется условием регулярности. Числа
называется условием регулярности. Числа  называются множителями Лагранжа. Функция Лагранжа, для которой
называются множителями Лагранжа. Функция Лагранжа, для которой  , называется регулярной.
, называется регулярной.
Теорема 7 (Необходимое условие локальной оптимальности второго порядка)
Пусть функции  дважды дифференцируемы в точке
дважды дифференцируемы в точке  и непрерывно дифференцируемы в некоторой её окрестности, причём градиенты
и непрерывно дифференцируемы в некоторой её окрестности, причём градиенты 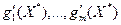 линейно независимы. Если
линейно независимы. Если 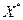 - локальное решение задачи (6), то
- локальное решение задачи (6), то
 (8)
(8)
при любых 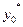 ,
,  , удовлетворяющих (7), и всех
, удовлетворяющих (7), и всех  таких, что
таких, что
 (9)
(9)
Теорема 8 (Достаточное условие локальной оптимальности)
Пусть функции  дважды дифференцируемы в точке
дважды дифференцируемы в точке  , удовлетворяющей ограничениям
, удовлетворяющей ограничениям  . Предположим, что при некоторых
. Предположим, что при некоторых 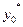 ,
,  выполняется условие (7), и кроме того
выполняется условие (7), и кроме того
 (10)
(10)
при всех ненулевых  , удовлетворяющих условию (9).
, удовлетворяющих условию (9).
Тогда 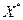 - строгое локальное решение задачи (6).
- строгое локальное решение задачи (6).
Пример 2.
Рассмотрим классическую задачу на условный экстремум:

 ,
,
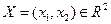 .
.
Решение:
1. Составим функцию Лагранжа:
 =
=  .
.
2. Выпишем необходимые условия оптимальности и ограничение задачи:

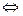

Ясно, что условие регулярности для данной задачи выполнено, но иногда бывает удобно рассмотреть отдельно два случая  и
и  .
.
Если  то и
то и  , что противоречит необходимому условию оптимальности (не все множители Лагранжа равны нулю). Полагаем
, что противоречит необходимому условию оптимальности (не все множители Лагранжа равны нулю). Полагаем  . Таким образом, имеем регулярную функцию Лагранжа:
. Таким образом, имеем регулярную функцию Лагранжа:
 =
=  .
.
Необходимые условия перепишутся в виде:

Данная система имеет два решения:
1) 
2) 
3. Далее рассмотрим матрицу вторых частных производных функции Лагранжа:
 .
.
Для указанных решений матрица принимает соответственно вид:
 ,
,  .
.
Выпишем условие (9):
 ,
,  .
.
Исследуем полученные точки  и
и  :
:
3.1. Условие (9) для точки  выглядит следующим образом:
выглядит следующим образом:  . Отсюда
. Отсюда  . Нетрудно проверить, что матрица
. Нетрудно проверить, что матрица  удовлетворяет условию (10). Достаточное условие оптимальности выполнено, следовательно, точка
удовлетворяет условию (10). Достаточное условие оптимальности выполнено, следовательно, точка  - строгое локальное решение исходной задачи.
- строгое локальное решение исходной задачи.
3.2. Из условия (9) для точки  получаем
получаем  . Проверим условие (8) для таких
. Проверим условие (8) для таких  . Получаем
. Получаем  , при
, при  . Необходимое условие оптимальности второго порядка не выполняется. Точка
. Необходимое условие оптимальности второго порядка не выполняется. Точка  не является решением задачи.
не является решением задачи.
19. Из данного треугольника вырезать два равных круга наибольшего радиуса.
20. Доказать, что из всех треугольников с общим углом при вершине и данной суммой длин боковых сторон равнобедренный треугольник имеет наименьшее основание.
21. Из всех треугольников с одинаковым основанием и одним и тем же углом при вершине найти треугольник с наибольшим периметром.
22. Даны две параллельные прямые и точка  между ними, лежащая на расстоянии
между ними, лежащая на расстоянии  от одной прямой и на расстоянии
от одной прямой и на расстоянии  от другой прямой. Точка
от другой прямой. Точка  служит вершиной прямых углов прямоугольных треугольников, две другие вершины которых лежат на каждой из параллельных прямых. Какой из треугольников имеет наименьшую площадь?
служит вершиной прямых углов прямоугольных треугольников, две другие вершины которых лежат на каждой из параллельных прямых. Какой из треугольников имеет наименьшую площадь?
23. В треугольной пирамиде проводятся сечения, параллельные двум её непересекающимся рёбрам. Найти сечение с наибольшей площадью.
24. Окно имеет форму прямоугольника, который сверху заканчивается полукругом. Каково должно быть основание прямоугольника для того, чтобы при данном периметре  окно пропускало бы больше света?
окно пропускало бы больше света?
25. Дан квадратный лист картона. Какой величины должны быть вырезаны квадраты в каждом из четырёх углов этого листа, чтобы из оставшейся крестообразный фигуры можно было сделать коробку наибольшей вместимости?
26. В эллипс  вписать прямоугольник наибольшей площади.
вписать прямоугольник наибольшей площади.
27. Из всех эллипсов, у которых сумма осей постоянна и равна  , найти наибольший по площади.
, найти наибольший по площади.
В задачах 28-31 требуется определить локальные минимумы и максимумы функции 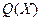 при выполнении ограничения
при выполнении ограничения  .
.
28. 
 ,
,  .
.
29.  ,
,  .
.
30.  ,
,  .
.
В задачах 28-30  .
.
31.  ,
,  ,
,  - симметрическая матрица размера
- симметрическая матрица размера  ,
,  .
.
32. Доказать, что для любых двух векторов  ,
,  таких, что
таких, что  ,
,  справедливо неравенство
справедливо неравенство  .
.
Найти решения задач на условный экстремум:
33.  ,
, 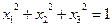 ,
,  .
.
34.  ,
,  ,
, 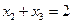 .
.
35. 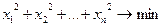 ,
,  .
.
- Число
 разложить на
разложить на 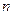 множителей так, чтобы сумма их была наименьшей.
множителей так, чтобы сумма их была наименьшей.