Основные правила проектирования стальных конструкций содержатся в Еврокоде EN 1993-1-1 (далее – Еврокод 3). В соответствии с этими нормами расчетное сопротивление стали получают делением характеристического значения сопротивления на коэффициент надежности по материалу
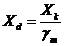
| (47) |
Но фактически в Еврокоде 3 расчеты ведутся по сопротивлению сечения
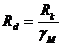
| (48) |
где Rd – расчетное сопротивление сечения;
Rk – характеристическое сопротивление сечения.
В таблице 13 приведены классы горячекатаной стали и соответствующие им значения предела текучести и предела прочности при растяжении.
Т а б л и ц а 13 – Номинальные значения предела текучести и предела прочности при растяжении для горячекатаной стали по EN 10025-2
| Номинальный класс стали | Номинальная толщина элемента 
| |||
| 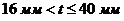
| |||
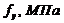
| 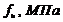
| 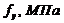
| 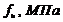
| |
| S235 | ||||
| S275 | ||||
| S355 | ||||
| S450 |
Коэффициенты надежности по материалу γ M:
для прочности сечения γ M = 1,0;
для расчета на устойчивость γ M = 1,0;
для прочности сечения на разрыв γ M = 1,1.
В Еврокоде 3 дается следующее определение четырем классам поперечных сечений:
- класс 1 – сечения, в которых может образовываться пластический шарнир с требуемой для пластического расчета способностью к повороту без снижения сопротивления сечения;
- класс 2 – сечения, в которых могут развиваться пластические деформации, но способность к повороту ограничена потерей местной устойчивости;
- класс 3 – сечения, в которых напряжение в крайних сжатых волокнах стального элемента при упругом распределении напряжений может достигнуть предела текучести, но потеря местной устойчивости предшествует развитию пластического сопротивления изгибающему моменту;
- класс 4 – поперечные сечения, в которых потеря местной устойчивости происходит прежде достижения предела текучести в какой-либо одной или более областях поперечного сечения.
Классификация сечения зависит от соотношений размеров его сжатых частей (таблица 14).
Т а б л и ц а 14 – Классификация сечений
| Тип элемента | Класс элемента | ||
| Класс 1 | Класс 2 | Класс 3 | |
| Вылет полки для прокатного профиля | 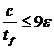
| 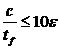
| 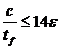
|
| Толщина стенки с нейтральной осью в середине высоты, прокатный профиль | 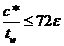
| 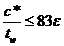
| 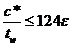
|
| Сжатая стенка, прокатный профиль | 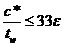
| 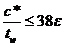
| 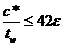
|
| |||
| 0,92 | 0,81 | |
| c *= d (см.рис. 1); c =(b - tw -2 r)/2 |
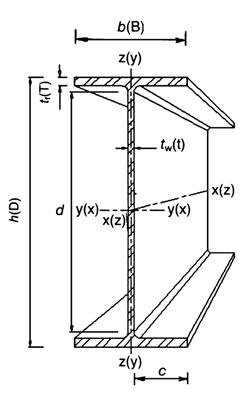
Рисунок 1 – Условные обозначения размеров поперечного сечения
Параметр ε вычисляется по формуле
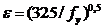
| (49) |
Для раскрепленных балок с раскрепленным верхним поясом необходимо выполнить следующие проверки:
- сопротивления поперечного сечения изгибу;
- устойчивости при сдвиге;
- устойчивости сжатой полки;
- сопротивления стенки поперечным усилиям;
- прогибов.
1. Сопротивление поперечного сечения изгибу.
При отсутствии или малой величине поперечной силы для всех сечений должной выполняться условие
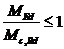
| (50) |
где M ed – расчетное значение изгибающего момента;
M c,Rd – расчетное сопротивление сечения изгибающему моменту, определяемое одним из следующих способов:
а) расчетное пластическое сопротивление изгибу сечения нетто:
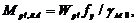
| (51) |
где W pl – пластический момент сопротивления сечения, устанавливается только для сечения 1 и 2 классов;
б) расчетное упругое сопротивление изгибу сечения нетто:
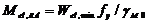
| (52) |
где W el,min – минимальный упругий момент сопротивления сечения, устанавливается только для сечения 3 класса;
в) расчетное сопротивление изгибу при потере местной устойчивости сечения нетто:
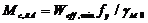
| (53) |
где W eff,min – минимальный эффективный момент сопротивления сечения, устанавливается только для сечения 4 класса;
г) расчетное предельное сопротивление изгибу сечения с отверстиями, если оно меньше значений, перечисленных выше.
2. Сопротивление поперечного сечения сдвигу.
Для всех сечений должно выполняться условие
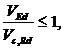
| (54) |
где V c,Rd – расчетное сопротивление поперечной силе. При выполнении пластического расчета V c,Rd принимается равным расчетному пластическому сопротивлению поперечной силе, определяемому по формуле
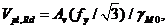
| (55) |
где Av рассчитывается для двутавровых сечений по формуле
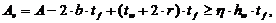
| (56) |
здесь A – площадь поперечного сечения;
b – ширина полки;
r – радиус внутреннего закругления;
t f – толщина полки;
t w – толщина стенки;
h w – высота стенки;
η = 1,0.
Для стенок, не усиленных ребрами жесткости, необходимо выполнять проверку на устойчивость при сдвиге в случае, если
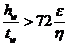
| (57) |
Для стенок, усиленных ребрами жесткости, необходимо выполнять проверку на устойчивость при сдвиге в случае, если
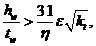
| (58) |
где – k τ – коэффициент устойчивости для сдвига, определяемый
при 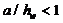
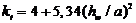
| (59) |
при 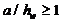
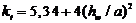
| (60) |
3. Сопротивление поперечному изгибу.
Пластическое сопротивление сечения изгибу снижается при наличии сдвига. В том случае, если действующая поперечная сила V Ed превышает 50% расчетного пластического сопротивления V pl,Rd расчетное сопротивление сечения изгибу M v,Rd должно вычисляться с пониженным пределом текучести, определяемом по формуле
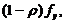
| (61) |
где
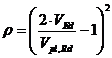
| (62) |
Тогда для прокатных двутавровых сечений сниженное расчетное сопротивление изгибу сечения
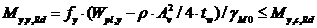
| (63) |
4. Сопротивление стенки потере устойчивости при сдвиге
Как было сказано ранее, эта проверка необходима в случае, если
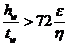
| (64) |
Для стандартных прокатных профилей в этой проверке, как правило, нет необходимости, так как отношение h w/ t w почти всегда оказывается менее 72ε.
5. Проверка по устойчивости сжатой полки.
Для исключения возможности потери устойчивости сжатой полки отношение h w/ t w должно удовлетворять условию
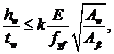
| (65) |
где A w – площадь стенки
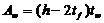
| (66) |
A fc – площадь сжатой полки
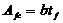
| (67) |
f yf – предел текучести стали сжатой полки.
Коэффициент kпринимается равным
0,3 – для полок класса 1;
2 – для полок класса 2;
0,55 - для полок классов 3 и 4.
6. Сопротивление стенки поперечным усилиям
Еврокоды различают два вида усилий, передающихся через полку на стенку:
а) силы, воспринимаемые за счет сопротивления стенки сдвигу (рисунок 2а и в);
б) силы, передающиеся через стенку напрямую на другую полку (рисунок 2б).
Расчетное сопротивление стенки местной потере устойчивости вычисляется по формуле
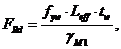
| (68) |
где f yw – предел текучести стали стенки;
t w – толщина стенки;
γ M1=1,0 – коэффициент надежности;
L eff – расчетная длина стенки
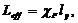
| (69) |
здесь χ F – понижающий коэффициент, учитывающий потерю местной устойчивости;
l y – расчетная длина площадки приложения нагрузки.
| а) | б) | в) |
| ||
| Рисунок 2 – Виды поперечных усилий, передающихся на стенку и вызывающих потерю устойчивости |
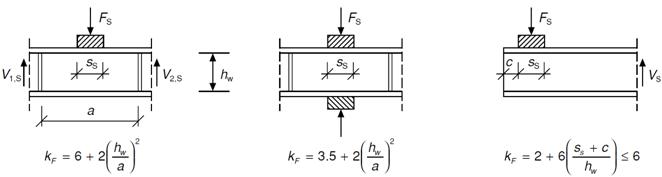
Согласно разделу 6.4 Еврокода 3 коэффициент χ F вычисляется по формуле
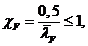
| (70) |
где
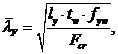
| (71) |
здесь
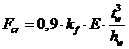
| (72) |
Для балок без горизонтальных ребер жесткости k F определяется по рисунку 7, а расчетная длина l y определяется следующим образом. Для типов загружения (а) и (б) на рисунке 7
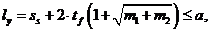
| (73) |
где
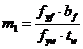
| (74) |
при 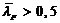
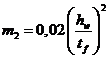
| (75) |
при 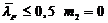
Для типа загружения (в) l y принимается равным меньшему из
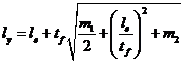
| (76) |
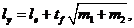
| (77) |
где
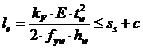
| (78) |
Если стенка подвержена совместному действию изгиба и сдвига, то должно выполняться условие
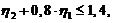
| (79) |
где
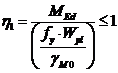
| (80) |
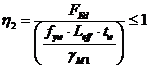
| (81) |
Задание 6
Выполнить проверки по прочности и жесткости однопролетной балки с сечением по сортаменту BritishUniversalBeams (сортамент – см. табл. 16), на которую действуют равномерные погонные нагрузки g k и q k. Исходные данные выбираются из таблицы 15. Балка защемлена по концам против поворота вокруг собственной оси. Длина площадок опирания равна 100 мм. Собственным весом балки пренебречь.
Т а б л и ц а 15 – Исходные данные для решения задания 6
| № вар. | Пролет балки l, м | Профиль UB | Постоянная нагрузка g k | Временная нагрузка q k |
| 305x102x25 | ||||
| 406x178x54 | ||||
| 457x191x74 | ||||
| 305x102x28 | ||||
| 457x191x82 | ||||
| 533x210x92 | ||||
| 305x102x33 | ||||
| 406x178x60 | ||||
| 457x191x89 | ||||
| 533x210x101 | ||||
| 406x178x67 | ||||
| 533x210x109 |
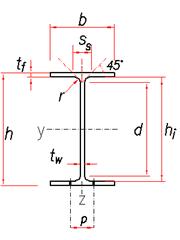
Рисунок 3 – Поперечное сечение профиля UniversalBeam
Т а б л и ц а 16 – Сортамент двутаврового профиля UniversalBeam
| Обозначение, мм∙мм∙кг/м | h,мм | b, мм | t w, мм | t f, мм | r, мм | m, кг/м | A, 103 мм2 | h / t f | h w, мм |
| 305x102x25 | 305.1 | 101.6 | 5.8 | 6.7 | 7.6 | 24.8 | 3.12 | 44.8 | |
| 305x102x28 | 308.9 | 101.9 | 6.1 | 8.9 | 7.6 | 28.2 | 3.64 | 34.7 | |
| 305x102x33 | 312.7 | 102.4 | 6.6 | 10.8 | 7.6 | 32.8 | 4.18 | ||
| 305x165x40 | 303.8 | 165.1 | 6.1 | 10.2 | 8.9 | 40.3 | 5.16 | 29.8 | |
| 305x165x46 | 307.1 | 165.7 | 6.7 | 11.8 | 8.9 | 46.1 | 5.88 | ||
| 305x165x54 | 310.9 | 166.8 | 7.7 | 13.7 | 8.9 | 6.82 | 22.7 | ||
| 356x171x45 | 6.9 | 9.7 | 10.2 | 5.7 | 36.3 | ||||
| 356x171x51 | 355.6 | 171.5 | 7.3 | 11.5 | 10.2 | 6.46 | 30.9 | ||
| 356x171x57 | 358.6 | 172.1 | 10.2 | 7.22 | 27.6 | ||||
| 356x171x67 | 173.2 | 9.1 | 15.7 | 10.2 | 67.1 | 8.55 | 23.2 | ||
| 406x140x39 | 397.3 | 141.8 | 6.3 | 8.6 | 10.2 | 4.92 | 46.2 | ||
| 406x140x46 | 402.3 | 142.4 | 6.9 | 11.2 | 10.2 | 5.9 | 35.9 | ||
| 406x178x54 | 402.6 | 177.6 | 7.6 | 10.9 | 10.2 | 54.1 | 6.86 | 36.9 | |
| 406x178x60 | 406.4 | 177.8 | 7.8 | 12.8 | 10.2 | 60.1 | 7.61 | 31.7 | |
| 406x178x67 | 409.4 | 178.8 | 8.8 | 14.3 | 10.2 | 67.1 | 8.55 | 28.6 | |
| 406x178x74 | 412.8 | 179.7 | 9.7 | 10.2 | 74.2 | 9.53 | 25.8 | ||
| 457x191x67 | 453.6 | 189.9 | 8.5 | 12.7 | 10.2 | 67.1 | 8.55 | 35.7 | |
| 457x191x74 | 457.2 | 190.5 | 9.1 | 14.5 | 10.2 | 74.3 | 9.51 | 31.5 | |
| 457x191x82 | 460.2 | 191.3 | 9.9 | 10.2 | 10.5 | 28.8 | |||
| 457x191x89 | 463.6 | 10.6 | 17.7 | 10.2 | 89.3 | 11.4 | 26.2 | ||
| 457x191x98 | 467.6 | 192.8 | 11.4 | 19.6 | 10.2 | 98.3 | 12.5 | 23.9 | |
| 533x210x82 | 528.3 | 208.7 | 9.6 | 13.2 | 12.7 | 82.2 | 10.5 | ||
| 533x210x92 | 533.1 | 209.3 | 10.2 | 15.6 | 12.7 | 92.1 | 11.8 | 34.2 | |
| 533x210x101 | 536.7 | 210.1 | 10.9 | 17.4 | 12.7 | 12.9 | 30.8 | ||
| 533x210x109 | 539.5 | 210.7 | 11.6 | 18.8 | 12.7 | 13.9 | 28.7 | ||
| 533x210x122 | 544.6 | 211.9 | 12.8 | 21.3 | 12.7 | 15.6 | 25.6 |