2.1. Найти коэффициенты квадратичного многочлена 
, зная, что 
, 
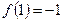и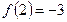 
.
2.2. Найти фундаментальную систему решений и записать общее решение системы линейных однородных уравнений: 
.
2.3. При каком значении параметра 
система линейных уравнений
является совместной?
2.4. Среди многочленов степени, не превосходящей 2, найти два линейно независимых многочлена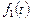 
и 
таких, что 
.
3. Линейные пространства.
3.1. Для множества положительных вещественных чисел операции сложения и умножения на вещественное число определены как «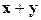
» = 
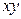и «
»= 
. Является ли указанное множество с такими операциями линейным пространством? В случае положительного ответа найти его размерность и указать базис.
3.2. В пространстве 
даны два базиса 
и 
с координатами базисных векторов в стандартном базисе 
, 
, 
и 
, 
, 
.
1) Найти матрицу перехода 
от базиса к базису .
2) Найти матрицу обратного перехода.
3) Найти координаты элемента 
в обоих базисах.
4) Найти координаты 
элемента 
в базисе , если его координаты в базисе 
есть 
.
3.3.Выяснить, является ли множество 
векторов пространства 
, все координаты которых равны между собой, подпространством линейного пространства, и если является, то найти его размерность.
3.4. Найти размерность суммы и пересечения подпространств 
и 
, являющихся линейными оболочками векторов 
и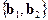 
:
, 
;
, 
.
3.5. Могут ли векторы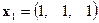 
, 
и 
образовать базис в трёхмерном пространстве? Построить с помощью данной системы векторов ортонормированный базис.
3.6. В комплексном пространстве 
со скалярным произведением 
построить базис в ортогональном дополнении 
подпространства 
, если компоненты векторов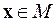 
удовлетворяют уравнению 
и 
.
Линейные операторы.
4.1. Выяснить, является ли данное преобразование пространства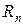 
линейным: 
, 
.
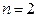4.2. Записать в декартовом базисе трёхмерного пространства матрицу оператора проектирования на прямую линию, заданную уравнением 
.
4.3. Записать в базисе из тригонометрических функций 
матрицу оператора дифференцирования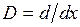 
.
4.4. Найти собственные значения и собственные вектора оператора, заданного своей матрицей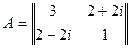 
.
4.5. Найти вид оператора с матрицей Паули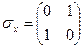 
в собственном базисе оператора с матрицей Паули 
.
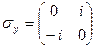4.6. Найти собственные функции и собственные значения оператора 
, где 
.
4.7. Найти сопряжённый оператор к линейному оператору 
, осуществляющему поворот на угол 
вокруг прямой 
в пространстве 
.
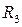Квадратичные формы.
5.1. Привести квадратичную форму от трёх переменных 
в пространстве 
к каноническому виду методом Лагранжа, найдя канонические коэффициенты и преобразование базиса.
5.2. При каких значениях параметра 
квадратичная форма 
является (а) положительно определённой и (б) отрицательно определённой?
5.3. Пусть 
- квадратичная форма в пространстве 
. Является ли подпространством 
множество 
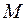векторов 
таких, что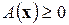 
? Рассмотреть в качестве примера форму 
в трёхмерном пространстве.
6.4. Методические материалы, определяющие процедуры оценивания
1. Положение «О проведении текущего контроля успеваемости и промежуточной аттестации обучающихся в ННГУ», утвержденное приказом ректора ННГУ от 13.02.2014 №55-ОД.
2. Положение о фонде оценочных средств, утвержденное приказом ректора ННГУ от 10.06.2015 №247-ОД.