Турбулентное течение в некруглых трубах

На практике часто приходится иметь дело с турбулентным течением в некруглых трубах, применяемых, например, в охлаждающих устройствах (радиаторах, теплообменниках, охлаждающих трактах двигателей и др.).

Линия соприкосновения жидкости в живом сечении с поверхностями, ограничивающими поток, называется смоченным периметром. В полностью заполненных круглых трубах длина смоченного периметра χ равна периметру сечения. Если труба заполнена не полностью,смоченный периметр составляет часть полного периметра.

Гидравлическим радиусом называется отношение площади живого сечения к смоченному периметру в этом сечении

где ω – живое сечение, χ – смоченный периметр.

Рис.11.9 Определение гидравлического радиуса.

В напорном потоке, заполняющем все (рис.11.9а) круглое сечение, где d, r –геометрические диаметр и радиус, гидравлический радиус равен

Гидравлический радиус равен Rг = 0,5r половине геометрического радиуса, четверти геометрического диаметра.Гидравлический диаметр равен четырем гидравлическим радиусам.

При неполном заполнении круглой трубы (рис.11.9б), например, на высоту радиуса

В прямоугольном потоке при полном заполнении сечения(рис.11.9), ширина b, высота сечения – h

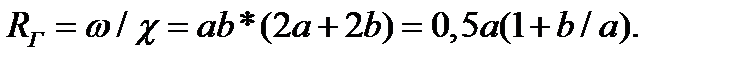
При неполном заполнении сечения (рис.11.9г)

Рассмотрим расчет потерь на трение при турбулентном течении в трубе с поперечным сечением произвольной формы. Суммарная сила трения, действующая на внешнюю поверхность потока длиной l,

Т = П*l*τ₀,

где П — периметр сечения; τ₀ - касательное напряжение на стенке, зависящее в основном от динамического давления,т.е. от средней скороститечения и плотности жидкости.

Расход жидкости и заданная площадь сечения Sопределяют среднюю скорость. Сила трения пропорциональна периметру сечения.

1)Для прямоугольника со сторонами abполучим S=ab, П = 2(a+b),

Rг = S/П = (ab)/(2(a+b)).

Dг = 4Rг = 4*(аb)/2(a+b) = 2*(аb)/(a+b)

2)ДляквадратаRг = S/П = (a²)/(4a) = a/4,Dг = 4*(а/4) = а

3)Для зазора а, при а<<b:Rг = S/П =

Dг = 4Rг = 4*(а/2)=2а

Для круглого сечения:Rг = S/П = 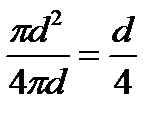. Откуда Dг = 4Rг.

Для определения потерь при турбулентном и при ламинарном режиме можно пользоваться формулой Вейсбаха—Дарси. Таким образом, для любой формы сечения

(10.9)

При этом коэффициент λ_т подсчитывают по тем же формулам, а число Рейнольдса выражают через гидравлический диаметр D_г:

Re = (VD_г)/ν.

11.10. Задача на простой трубопровод.

Поршень диаметром D=200мм движется вверх в цилиндре, засасывая воду, из открытого резервуара с постоянным уровнем. Диаметр и коэффициент сопротивления трубопроводов: d=50мм, l=4м, λ=0.03. Коэффициенты сопротивления каждого колена ξк=0,5, когда поршень находится на высоте h=2м относительно резервуара, сила для его перемещения равна F=2350H. Определить: скорость подъема поршня, и найти до какой высоты h можно поднимать поршень с такой скоростью без опасности отрыва жидкости от поршня, если давление насыщенных паров равно рн.п.=4,25кПа, ρ=995кг/м³, ратм=98,7кПа.

Решение
1.Ур-е Б. для свободной поверхности резервуара 0-0, и для плоскости 1-1, совпадающей с плоскостью поршня.Плоскость сравнения по 0-0, в избыточных давлениях.

1.1. Скорость поршня

2. Уравнение неразрывности

2.1.Скорость в трубопроводе V_ТР через скорость поршняV_П

где V _П –скорость поршня, V_ТР -скорость в трубопроводе.

3.Коэффициент суммарных потерь в трубопроводе через скорость в трубопроводе

3. Определяем скорость поршня из у-я Б., считая α = 1.

4.Определение предельной величины h. Для обеспечения нормальной (бескавитационной) работы тру­бопровода должно выполняться условие ограничивающее давление в поршне. Чтобы не было отрыва должно выполняться условие Р_н.п<Р_ат –Р_П, откуда

Р_П<Р_ат –Р_н.п.

где Р_ат - атмосферное давление; Р_н.п.- давление насыщенных паров жидкости при данной температуре. Определим минимальное значение давления под поршнем

Р_П = Р_ат – Р_н.п.= 98,7 – 4,25 = 94,45 кПа.

5.Подставим это значение в уравнение 4.