Дискретная случайная величина и закон ее распределения.
Дискретной случайной величиной называется всякая величина, которая в результате опыта принимает числовое значение:
Пример:
- число очков при бросании игральной кости
- число лепестков на цветке сирени
- температура воздуха в определенное время дня
Так как каждое значение случайной величины встречается с различной частотой, то все значения необходимо рассматривать с вероятностями появления этих значений. Когда известны все значения случайной величины и вероятности их появления, то говорят, что задан закон распределения случайной величины. Закон распределения обычно записывают в виде таблицы:
| Х |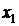 
| 
| 
| … | 
|
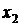
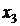
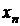
| р |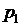 
| 
| 
| … | 
|
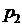
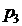
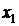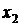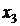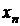, , ,… – значения случайной величины (СВ)
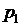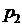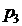, , , …. – соответствующие значения вероятностей СВ
Закон составлен верно, если: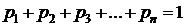 
Пример 1:
Составить закон распределения числа очков при бросании игральной кости.
Решение:
Х – число очков при бросании игральной кости
Так как у игральной кости 6 граней, то возможно всего шесть числовых значений: 1, 2, 3, 4, 5, 6.
Найдем вероятности каждого значения. Вероятность, что выпадет 1 очко, равна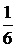 
. Для остальных значений получим такие же вероятности:
Получаем закон:
| Х | ||||||
| р |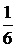
|
|
|
|
|
|
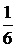
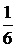
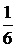
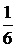
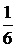
Проверим правильность выполнения закона: + + + + + =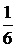 
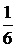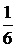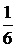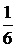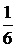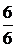=1
Характеристики случайной величины.
К основным характеристикам случайной величины относят математическое ожидание, дисперсию и среднее квадратическое отклонение:
Математическое ожидание – это сумма произведений значений случайной величины, на соответствующие вероятности этих значений:
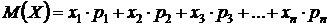
Математическое значение показывает среднее значение случайной величины.
Дисперсия – это математическое ожидание квадрата отклонений значений случайной величины от их математического ожидания:
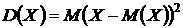
Для вычисления дисперсии удобнее пользоваться формулой: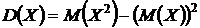 
, где:
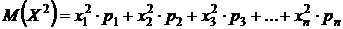
Среднее квадратическое отклонение – это арифметический квадратный корень из дисперсии: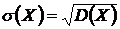 
Среднее квадратическое отклонение показывает на сколько отклоняются остальные значения случайной величины от среднего.
Пример №2:
Задан закон распределения дискретной случайной величины X (в первой строке указаны возможные значения величины X, во второй строке – вероятности pi этих возможных значений). Найти математическое ожидание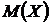 
, дисперсию 
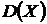, среднее квадратическое отклонение 
.
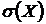| х | ||||
| р | 0,2 | 0,4 | р | 0,1 |
Решение:
Для решения задачи найдем неизвестное р:
Известно, что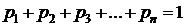
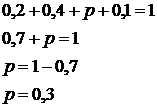
1) Математическое ожидание случайной величины:
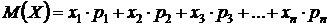
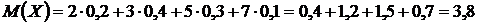
2). Дисперсию вычислим по формуле: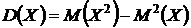 
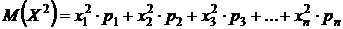
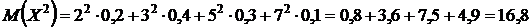
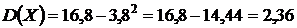
3) 
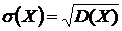– среднеквадратическое отклонение.
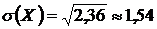
Свойства математического ожидания и дисперсии
Пусть:
Свойства математического ожидания:
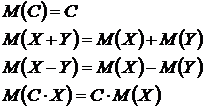
| Свойства дисперсии:
|
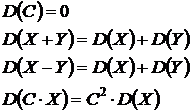
Пример №3:
Пусть по условию задачи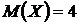 
, 
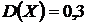. Найт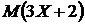и: 
и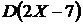 
Решение:
Применим свойства математического ожидания:
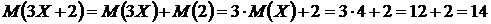
Применим свойства дисперсии:
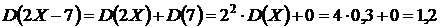
Задания для самостоятельного решения:
1. Дискретная случайная величина X имеет распределение, представленное таблицей:
| X | -2 | -1 | |||
| p | 0,1 | 0,2 | 0,3 | р | 0,2 |
Найти р.
2. Найти M(X), D(X), σ(X), зная закон распределения дискретной случайной величины:
| X | ||||
| p | 0,4 | 0,2 | 0,15 | 0,25 |
3. Даны две случайные величины X и Y, причем M(X) =5, M(Y) =3. Найти математическое ожидание случайной величины Z = X + 2Y.
4. Случайные величины X и Y независимы. Найти дисперсию случайной величины Z=3X+2Y, если известно, что D(X)=5, D(Y)=6.
Ответы для самоконтроля:
1) р =0,2
2 ) М(Х)=7,3 D(Х)=62,91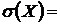 
7,93;
3 ) М(Z)=11;
4 ) D(Z)=69