Аннотация. Данная тема раскрывает особенности адаптивных моделей временных рядов.
Ключевые слова. Адаптивная модель, экспоненциальное сглаживание, параметр адаптации.
Методические рекомендации по изучению темы
· Тема содержит лекционную часть, где даются общие представления по теме.
· В качестве самостоятельной работы предлагается выполнить практические задания и ответить на вопросы для самоконтроля.
· Для проверки усвоения темы имеется тест для самоконтроля.
Рекомендуемые информационные ресурсы:
1. https://tulpar.kpfu.ru/mod/resource/view.php?id=11766
2. Эконометрика: учебник / И. И. Елисеева. – M.: Проспект, 2010. – 288 с. С.200-205.
3.Эконометрика: [Электронный ресурс] Учеб. пособие / А.И. Новиков. - 3-e изд., испр. и доп. - М.: ИНФРА-М, 2014. - 272 с.: (https://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=1#none) С. 96-113.
4. Эконометрика. Практикум: [Электронный ресурс] Учебное пособие / С.А. Бородич. - М.: НИЦ ИНФРА-М; Мн.: Нов. знание, 2014. - 329 с. (https://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С.276-278.
5. Эконометрика: учебник / под ред. В. С. Мхитаряна. - М.: Проспект, 2008. -384 с. С.297-325.
6. Электронный курс “Time Series Econometrics”, Princeton University, URL: https://sims.princeton.edu/yftp/Times05/;https://blackboard.princeton.edu/webapps/portal/frameset.jsp?tab_group=courses&url=%2Fwebapps%2Fblackboard%2Fexecute%2FcourseMain%3Fcourse_id%3D_52968_1.
Глоссарий
Коэффициент сезонности – коэффициент, учитывающий в адаптивной модели сезонную составляющую; используется в адаптивных моделях в аддитивной и мультипликативной формах.
Параметр адаптации - параметр сглаживания a, который минимизировал бы ошибку предсказания.
Экспоненциальное сглаживание – процедура, которая приводит к адаптивному механизму, построенному на принципе регулятора с обратной связью.
Вопросы для изучения
1. Адаптация в моделях временных рядов. Построение адаптивных моделей линейного роста.
2. Адаптивные модели с учетом аддитивных и мультипликативных сезонных составляющих.
3. Процедуры подбора параметров адаптивных моделей временных рядов.
Адаптация в моделях временных рядов. Построение адаптивных моделей линейного роста. Примером модели, для которой можно построить различные варианты адаптивных механизмов, как раз и является адаптивный полином первой степени xt+t=a1t+ a2t t+ et+t. Ее адаптивный механизм предусматривает расчет оценок текущих (т. е. на данный момент времени) коэффициентов модели по двум рекуррентным соотношениям:
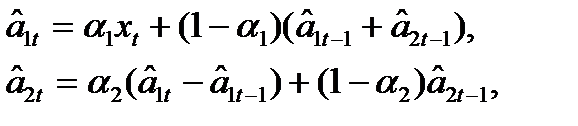
где a1,a2 – параметры экспоненциального сглаживания (0<a1, a2<1). Используемая в рекуррентных соотношениях процедура экспоненциального сглаживания приводит, как и в случае полинома нулевой степени, к адаптивному механизму, построенному на принципе регулятора с обратной связью.
Адаптивные модели с учетом аддитивных и мультипликативных сезонных составляющих. Модели с мультипликативным коэффициентом сезонности: 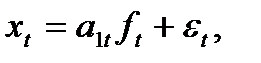 где a1t – изменяющийся во времени коэффициент, динамика которого характеризует тенденцию развития процесса;ft, ft-1, …, ft-l+1 – коэффициенты сезонности;l – количество фаз в полном сезонном цикле (при месячных наблюдениях l=12, при квартальных – l=4). Модели с аддитивным коэффициентом сезонности:
где a1t – изменяющийся во времени коэффициент, динамика которого характеризует тенденцию развития процесса;ft, ft-1, …, ft-l+1 – коэффициенты сезонности;l – количество фаз в полном сезонном цикле (при месячных наблюдениях l=12, при квартальных – l=4). Модели с аддитивным коэффициентом сезонности: 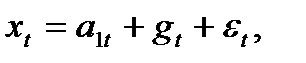 где gt, gt-1, …, gt-l+1 – адаптивные коэффициенты сезонности. Если моделируемый процесс имеет тенденцию линейного роста, то в указанных моделях член, соответствующий полиному нулевого порядка, заменяется полиномом первого порядка, и тогда модели записываются в следующем виде:
где gt, gt-1, …, gt-l+1 – адаптивные коэффициенты сезонности. Если моделируемый процесс имеет тенденцию линейного роста, то в указанных моделях член, соответствующий полиному нулевого порядка, заменяется полиномом первого порядка, и тогда модели записываются в следующем виде: 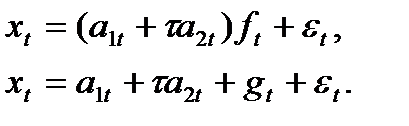
Расчет текущих оценок коэффициентов всех этих моделей осуществляется с использованием принципа экспоненциального сглаживания.
Процедуры подбора параметров адаптивных моделей временных рядов. Основное внимание уделяется выбору такой величины параметра сглаживания a, которая минимизировала бы ошибку предсказания. Выбор величины этого параметра в зависимости от количества наблюдений m, входящих в интервал сглаживания, по формуле: a=2/(m+1) малопригоден для практического использования.
Наиболее часто используемой процедурой подбора оптимальной величины a является метод проб. Общая схема этой процедуры предусматривает деление временного ряда на две части: обучающую и контрольную. Затем по обучающей части при различных a строятся прогнозные модели и делаются расчеты на период, отведенный под контрольную часть. Для каждого a расчетные значения сравниваются с фактическими значениями контрольной части, и определяется среднеквадратическая ошибка прогноза. Оптимальным считается то a*, для которого эта ошибка оказалась минимальной. Все прогнозные расчеты осуществляются с использованием оптимального значения сглаживающего параметра. В тех случаях, когда оптимальный уровень параметра a с течением времени подтвержден изменениями, эффективность этого подхода снижается, так как оптимум по обучающейся части может не совпадать с оптимумом по всему временному ряду. Еще одной интересной процедурой оптимальной настройки изменяющегося во времени параметра сглаживания является метод адаптивного градиентного экспоненциального сглаживания, так как в его основе лежит применение градиентной оптимизации для поиска оптимальных значений параметра at в адаптивных моделях, использующих принцип экспоненциального сглаживания.
Вопросы и задания для самоконтроля
1. В чем заключаются сущность, механизмы и формы адаптации в социально-экономических системах?
2. В чем заключается специфика экспоненциального сглаживания?
3. В чем состоит особенность модели с мультипликативным коэффициентом сезонности?
4. Какова особенность модели с аддитивным коэффициентом сезонности?
5. Как оценивается коэффициент сезонности для модели, учитывающей тенденцию линейного роста?
6. Какие модели включает группа адаптивных моделей с сезонными составляющими?
7. Какие особенности включает процедура подбора сглаживающего параметра методом проб?
8. В чем заключаются особенности процедуры подбора сглаживающего параметра методом градиентной оптимизации?
Задача 1. Имеются данные о потреблении мороженого, тыс. руб.:
| Сезон | Год | ||||
| Зима | 253,1 | 265,5 | 277,9 | 290,3 | 301,3 |
| Весна | 331,2 | 343,6 | 356,0 | 368,4 | 375,4 |
| Лето | 364,3 | 376,7 | 389,1 | 401,5 | 412,4 |
| Осень | 292,4 | 304,8 | 317,2 | 343,2 | 337,5 |
Задание: постройте адаптивную модель с линейным трендом и аддитивной сезонной компонентой для прогнозирования потребления мороженого.
Лекция 19