Задание 1
Найти указанные пределы:
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
Задание № 2
Найти производные, пользуясь правилами и формулами дифференцирования:
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
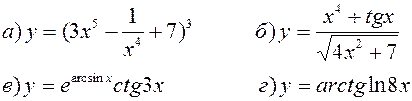
Задание № 3
Исследовать заданные функции методами дифференциального исчисления, начертить их графики.
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
 
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
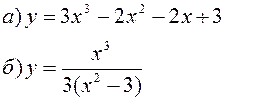
Контрольная работа № 2
Решение типовых примеров
Задание № 1
1. Найти неопределенный интеграл 
Решение. Применим подстановку 
, тогда 
и
;
2. Найти интеграл 
.
Решение. Применим подставку t =3 x 3 – 5.
Тогда 
; 
, откуда
.
Задание № 2
Найти интеграл 
Решение. Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом:
x 2 – 6 x +13 = x 2 – 6 x + 9 + 4 = (x - 3)2 + 22. Тогда после подстановки t = x - 3 получаем
причем, при вычислении интеграла 
воспользуемся заменой переменной z = t 2+4, тогда dz = 2 tdt, откуда
.
Итак, учитывая, что t = x – 3, имеем
.
Задание № 3
1. Найти интеграл 
.
Решение. Применим формулу интегрирования по частям
Положим
u = 3 x +7, dv = cos5 xdx,
тогда
du = 3 dx, 
.
Следовательно,
.
2. Найти интеграл 
.
Решение.
Положим
u = arctg 4 x, dv = dx,
тогда
v = x.
Отсюда
.
Применяя в последнем интеграле подстановку t = 1+16 x 2,
получаем, 
, следовательно,
.
Отсюда 
.
Задание № 4
Вычислить площадь, ограниченную параболами
y = 2 x 2 – x – 2,
y = - x 2 + x – 1.
Решение.
Рисунок 2 – График построения парабол
Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
2 x 2 – x – 2 = - x 2 + x – 1. Отсюда 3 x 2 – 2 x – 1 = 0, D = 4 + 4∙3 = 16,
, 
Вычисление площади осуществляем по формуле:
,
где f 1(x), f 2(x) – кривые, ограничивающие фигуру (f 2(x) ³ f 1(x)).
В нашем случае
Распределение заданий
Таблица 2 – Распределение заданий для контрольной работы № 2
| Предпоследняя цифра шифра | № задания | Последняя цифра шифра | |||||||||
| 2 4 | |||||||||||
| 1 4 | |||||||||||
| 1 7 | |||||||||||
Задания к контрольной работе № 2
Задание №1
Найти неопределенные интегралы способом подстановки (методом замены переменной)
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
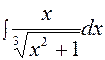
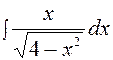
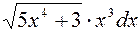
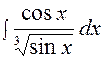
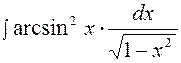
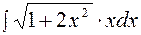
Задание №2
Найти неопределенные интегралы, используя выделение полного квадрата
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
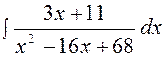
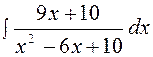
Задание № 3
Найти неопределенные интегралы, используя метод интегрирования по частям
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
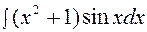
Задание № 4
Вычислить площадь, ограниченную заданными параболами
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
Теоретические вопросы
1. Понятие предела функции в точке и в бесконечности.
2. Основные теоремы о пределах. Раскрытие неопределенностей при вычислении пределов.
3. Непрерывность функции в точке и на интервале.
4. Определение производной, ее геометрический смысл.
5. Правила вычисления производной. Таблица производных.
6. Исследование функции на интервалы монотонности. Точки экстремума.
7. Исследование функции на интервалы выпуклости. Точки перегиба.
8. Асимптоты кривой.
9. Общая схема исследования функции.
10. Дифференциал функции.
11. Применение дифференциала к приближенным
вычислениям.
12. Первообразная функции и неопределенный интеграл.
13. Правила вычисления неопределенного интеграла. Таблица интегралов.
14. Методы вычисления неопределенного интеграла.
15. Определенный интеграл. Формула Ньютона-Лейбница.
16. Основные свойства определенных интегралов.
17. Методы вычисления определенного интеграла.
18. Вычисление площадей плоских фигур.
19. Основные понятия теории вероятностей: события, вероятность события, частота события, случайная величина.
20. Сумма и произведение событий, теоремы сложения и умножения вероятностей.
21. Дискретные случайные величины. Ряд, многоугольник и функция распределения.
22. Непрерывные случайные величины. Функция и плотность распределения.
23. Формула полной вероятности.
24. Числовые характеристики случайных величин: дисперсия; и среднеквадратичное отклонение.
25. Понятия: группа, выборка, генеральная совокупность.
26. Эмпирическая функция распределения.
27. Вариационный ряд. Полигон частот и гистограмма
28. Точечные оценки. Выборочная средняя и выборочная дисперсия.
Приложения
Справочные материалы
Правила дифференцирования:
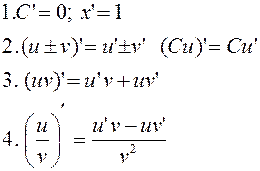
Производная сложной функции:
Таблица производных основных элементарных функций и производных сложных функций
| y = f (x) | y ¢ = f ′(x) | y = f (u), u = j(х) | у ¢ = f ′(u)× u ¢ |
| y = x a | (x a)¢ = a× x a-1 | y = u a | y ¢ = a× u a-1× u ¢ |
| 
| y = 
| 
|
| 
| 
| 
|
| y = ax | (ax)¢ = ax ×ln a | y = au | y¢ = au ×ln a×u ¢ |
| y = e x | (e x)¢ = e x | y = e u | y¢ = e u × u ¢ |
| y = log ax | (log ax)¢ 
| y =log au | 
|
| y = ln x | 
| y = ln u | 
|
| y = sin x | (sin x)¢ = cos x | y = sin u | y ¢ = cos u × u ¢ |
| y = cos x | (cos x)¢ = -sin x | y = cos u | y ¢ = -sin u × u ¢ |
| y = tg x | 
| y = tg u | 
|
| y = ctg x | 
| y = ctg u | 
|
| y = arcsin x | 
| y = arcsin u | 
|
| y = arccos x | 
| y = arccos u |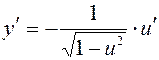 
|
| y = arctg x | 
| y = arctg u |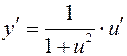 
|
| y = arcctg x | 
| y = arcctg u | 
|
Таблица основных интегралов
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|