Коэффициент локализации рассчитывается для каждой i-й составной совокупности. При равномерном распределении все значения 
. В случае концентрации значений признака в i-й составной 
, и наоборот.
Коэффициент концентрации является обобщающей характеристикой отклонения распределения от равномерного. Значения его колеблются в границах от 0 до 1. В равномерном распределении К=0. Чем более заметна концентрация, тем больше значение К отклоняется от 0. Расчет коэффициентов Li и К представлен в табл. 5.3 на примере распределения фермерских хозяйств по стоимости реализованной продукции.
Таблица 5.3
| Стоимость реализованной продукции, тыс. грн. | % к итогу | 
| 
| |
| количество ферм, di | стоимость реализованной продукции, Di | |||
| До 2 | 0,17 | |||
| 2–5 | 0,28 | |||
| 5–10 | 0,52 | |||
| 10–20 | 1,12 | |||
| 20-40 | 2,87 | |||
| 40 и больше | 8,00 | |||
| Всего | -- |
Коэффициент концентрации составляет
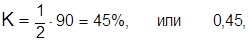
что свидетельствует об относительно высоком уровне концентрации товарного сельскохозяйственного производства в фермерских хозяйствах. Объемы товарной продукции концентрируются в больших хозяйствах – в последней группе 
.
Коэффициенты концентрации и локализации являются эффективным средством измерения дифференциации совокупности по данным интервальных рядов с неравными интервалами и по данным атрибутивных рядов. По аналогии с коэффициентом концентрации рассчитывают коэффициент подобия (сходства) структур двух объектов или одного объекта по двум признакам:
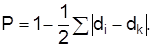
Если структуры одинаковые, Р=1. Чем большие отклонения структур, тем меньше значение коэффициента Р.
Для оценки интенсивности структурных сдвигов во времени используют абсолютные меры вариации – среднее линейное или среднее квадратичное отклонение частостей, которые называют коэффициентами структурных сдвигов:
линейный квадратичный
где: di 0 и di 1 – частости распределения за два периода;
m – число составляющих совокупности.
Расчет линейного коэффициента структурных сдвигов в промышленном потреблении алюминия приведен в табл. 5.4. По данным таблицы
т.е. структура промышленного потребления алюминия изменилась в среднем на 5,5 процентных пункта.
Таблица 5.4
| Отрасль потребления алюминия | % к итогу | Структурные сдвиги, процентные пункты | |
| 1985г. | 1995г. | ||
| Транспортное машиностроение | - 7 | ||
| Производство тары и упаковки | |||
| Производство товаров долгосрочного пользования | - 4 | ||
| Иное | |||
| Всего |
Дисперсия, в отличие от других характеристик вариации, является аддитивной величиной. Т.е. в структурируемой совокупности, которая разделена на группы по факторною признаку x, дисперсия результативного признака yможет быть разложена на: дисперсию в каждой группе (внутригрупповую) и дисперсию между группами (межгрупповую). Общая дисперсия характеризует вариацию признака y за счет воздействия всех причин (факторов), межгрупповая – за счет фактора х, положенного в основу группировки, а внутригрупповые – за счет других факторов, не учтенных в группировке.
Межгрупповая дисперсия вычисляется по формуле
,
где 
– соответственно средняя i-йгруппы и общая средняя варьирующего признака y; fi – частота i-й группы.
Внутригрупповая дисперсия рассчитывается отдельно для каждой i-й группы:
где y – значение признака отдельных элементов совокупности.
Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных частотами соответствующей группы:
Взаимосвязь между тремя дисперсиями получила название правила сложения дисперсий, согласно которому
Общую дисперсию можно определить и непосредственно по формуле
Отношение межгрупповой дисперсии к общей называется корреляционным отношением 
.
Расчет указанных дисперсий показан по данным табл. 5.5 на примере урожайности винограда.
Вариация урожайности отдельно для каждого сорта винограда определяется тремя внутригрупповыми дисперсиями. Для сорта винограда "Алиготе" внутригрупповая дисперсия составляет,
где 
Таблица 5.5
| Сорт винограда | Количество кустов, fi | Урожайность с одного куста, кг y | 
| 
|
| Алиготе | 2,3; 2,2; 2,7; 2,6; 2,2 | 2,4 | ||
| Фетяска | 2,9; 3,3; 2,7; 2,8;3,2; 3,4; 2,8; 2,9 | 3,0 | ||
| Рислинг | 3,6; 4,0; 4,1; 4,4; 3,8; 3,9; 4,2 | 4,0 | ||
| В целом | X | 3,2 |
Аналогично вычислены внутригрупповые дисперсии для второй и третьей групп: 
.
Средняя из групповых дисперсий равняется
Межгрупповая дисперсия составляет
где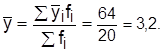 
Общую дисперсию урожайности определим по правилу составления дисперсий как сумму межгрупповойї и средней из групповых дисперсий:
Непосредственное вычисление общей дисперсии по упрощенной формуле
дает такой же самый результат.