Лабораторная работа №1. Простейшие задачи аналитической геометрии. Аналитическая геометрия на плоскости

1. Построить на чертеже отрезки, исходящие из начала координат, зная их проекции на координатные оси:

2. Построить на чертеже отрезки, имеющие началом точку M(2; -1), зная их проекции на координатные оси:

3. Вычислить проекцию отрезка на ось u, если даны его длина d и угол j наклона к оси:

4. Построить на чертеже отрезки, исходящие из начала координат, зная длину d и полярный угол q каждого из них:

5. Даны точки М₁(2; -3), M₂(1; -4), M₃(-1; -7), M₄(-4; 8). Вычислить длину и полярный угол следующих отрезков: , , ,

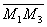6. Длина d отрезка равна 5, его проекция на ось абсцисс равна 4. Найти проекцию этого отрезка на ось ординат при условии, что он образует с осью ординат:Острый угол;Тупой угол.

7. Длина отрезка равна 13; его начало в точке М(3; -2), проекция на ось абсцисс равна –12. Найти координаты конца этого отрезка при условии, что он образует с осью ординат:Острый уголТупой угол.

8. Длина отрезка равна 17, его конец в точке N(-7; 3), проекция на ось ординат равна 15. Найти координаты начала этого отрезка при условии, что он образует с осью абсцисс:Острый угол;Тупой угол.

9. Даны две смежные вершины квадрата. Вычислить его площадь.

10. Даны две противоположные вершины квадрата. Вычислить его площадь.

11. Вычислить площадь правильного треугольника, две вершины которого суть.

12. Даны три вершины параллелограмма ABCD, четвертая вершина которого D противоположна B. Определить длины диагоналей того параллелограмма.

13. Доказать, что точки А(3; -5), В(-2; -7), С(18; 1) лежат на одной прямой.

14. Сторона ромба равна , две его противоположные вершины суть точки P(4; 9), Q(-2; 1). Вычислить площадь этого ромба.

15. Сторона ромба равна , две его противоположные вершины суть точки P(3; -4), Q(1; 2). Вычислить длину высоты этого ромба.

16. Доказать, что точки А(3; -5), В(-2; -7), С(18; 1) лежат на одной прямой.

17. Доказать, что треугольник с вершинами A₁(1; 1), A₂(2; 3), A₃(5; -1) прямоугольный.

18. Доказать, что точки А(2; 2), В(-1; 6), С(-5; 3), D(-2; -1) являются вершинами квадрата.

19. Определить, есть ли среди внутренних углов треугольника с вершинами M₁(1; 1), M₂(0; 2), M₃(2; -1) тупой угол.

20. Доказать, что все внутренние углы треугольника с вершинами M(-1; 3), N(1; 2), P(0, 4) острые.

21. Вершины треугольника суть точки A(5; 0), B(0; 1), C(3; 3). Вычислить его внутренние углы.

22. Вершины треугольника суть точки А(; 1), B(0, 2), C(; 2). Вычислить его внешний угол при вершине А.

23. На оси абсцисс найти такую точку М, расстояние от которой до точки N(2; -3) равнялось бы 5.

24. Даны две точки M(2; 2), N(5; -2); на оси абсцисс найти такую точку Р, чтобы угол MPN был прямым.

25. Через точку А(4; 2) проведена окружность, касающаяся обеих координатных осей. Определить ее центр С и радиус R.

26. На оси ординат найти такую точку М, расстояние от которой до точки N(-8; 13 равнялось бы 17.

27. Через точку М₁(1; -2) проведена окружность радиуса 5, касающаяся оси Ox. Определить центр С окружности.

28. Определить координаты точки М₂, симметричной точке М₁(1; 2) относительно прямой, проходящей через точки А(1; 0), В(-1; -2).

29. Даны две противоположные вершины квадрата А(3; 0) и С(-4; 1). Найти две его другие вершины.

30. Даны две смежные веришны квадрата А(2; -1) и В(-1; 3). Определить две его другие вершины.

31. Даны вершины треугольника M₁(-3; 6), M₂(9; -10), M₃(-5; 4). Определить центр С и радиус R круга, описанного около этого треугольника.

32. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет и уравнения директрис: ,

33. Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже. ,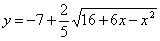

34. Составить уравнение эллипса, зная, что:его большая ось равна 26 и фокусы суть F₁(-10; 0), F₂(14;0);

35. Составить уравнение эллипса, зная, что:его малая ось равна 2 и фокусы суть F₁(-1; -1), F₂(1; 1);

36. Составить уравнение эллипса, зная, что:его фокусы суть F₁(-2; 3/3), F₂(2; -3/2) и эксцентриситет e= .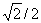

37. Составить уравнение эллипса, зная, что:его фокусы суть F₁(1; 3), F₂(3; 1) и расстояние между директрисами равно .

38. Составить уравнение эллипса, если известны его эксцентриситет , фокус F (-4; 1) и уравнение соответствующей директрисы

39. Составить уравнение эллипса, если известны его эксцентриситет e=1/2, фокус F(-4; 1) и уравнение соответствующей директрисы .

40. Точка А(-3; -5) лежит на эллипсе, фокус которого F(-1; -4), а соответствующая директриса дана уравнением . Составить уравнение этого эллипса.

41. Определить, при какихначениях m прямая :пересекает эллипс ;касается его;проходит вне этого эллипса.

42. Составить уравнение эллипса, если известны его эксцентриситет e=1/2, фокус F(3; 0) и уравнение соответствующей директрисы .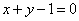

43. Точка M₁(2; -1) лежит на эллипсе, фокус которого F(1; 0), а соответствующая директриса дана уравнением . Составить уравнение этого эллипса.

44. Вывести условие, при котором прямая касается эллипса .

45. Найти точки пересечения прямой и эллипса .

46. Определить, как расположена прямая относительно эллипса: пересекает ли, касается или проходит вне его, если прямая и эллипс заданы следующими уравнениями: , ; , ;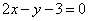

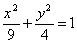47. Составить уравнения касательных к эллипсу , параллельных прямой .

48. Провести касательные к эллипсу параллельно прямой и вычислить расстояние d между ними.

49. На эллипсе найти точку М₁, ближайшую к прямой , и вычислить расстояние d от точки М₁ до этой прямой.

50. Эллипс, малая полуось которого равна 6, является проекцией окружности радиуса R=12. Опредилть угол 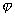между плоскостями, в которых лежат эллипс и окружность.

51. Направляющей круглого цилиндра является окружность радиуса R=8. Определить полуоси эллипса, полученного в сечении этого цилиндра плоскостью, наклоненной к его оси под уголом 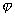=30⁰.

52. Направляющей круглого цилиндра является окружность радиуса R= . Определить, под каким углом к оси цилиндра нужно его пересечь плоскостью, чтобы в сечении получить эллипс с большой полуосью a=2.

53. Коэффициент равномерного сжатия плоскости к оси Oy равен 3/4. Определить уравнение линии, в которую при таком сжатии преобразуется эллипс .

54. Составить уравнения касательных к эллипсу , перпендикулярных к прямой .

55. Найти точки пересечения прямой и эллипса .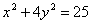

56. Доказать, что касательные к эллипсу , проведенные в концах одного и того же диаметра, параллельны. (Диаметром эллипса называется его хорда, проходящая через его центр).

57. Из точки А(10/3; 5/3) проведены касательные к эллипсу . Составить их уравнения.

58. Прямая касается эллипса, фокусы которого находятся в точках F₁(-3; 0), F₂(3; 0). Составить уравнение этого эллипса.

59. Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если известны уравнение касательной к эллипсу и его малая полуось b=2.

60. Определить точки пересечения эллипсов , .

61. Убедившись, что эллипсы , 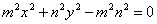() пересекаются в четырех точках, лежающих на окружности с центром в начале координат, определить радиус R этой окружности.

62. Плоскости и 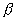образуют угол 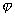=30⁰. Опредлить полуоси эллипса, полученного проектированием на плоскость 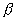окружности радиуса R=10,лежащей на плоскости .

63. Найти уравнение линии, в которую преобразуется эллипс при двух последовательных равномерных сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ox и Oy равны соответственно 4/3 и 6/7.

64. Определить коэффициент q равномерного сжатия плоскости к оси Ox, при котором эллипс преобразуется в эллипс .

65. Определить коэффициент q равномерного сжатия плоскости к оси Oy, при котором эллипс преобразуется в эллипс .

66. Определить коэффициенты q₁, q₂ двух последовательных равномерных сжатий плоскости к осям Ox и Oy, при которых эллипс преобразуется в окружность .