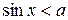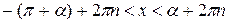Решение тригонометрических неравенств
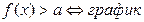 - означает, что график функции
- означает, что график функции 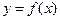 проходит выше прямой
проходит выше прямой
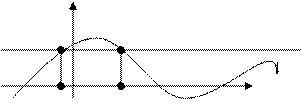 у = а на определенном множестве
у = а на определенном множестве 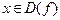
. у
у=а f(x)>a, xÎ(x1;x2)
F(x)
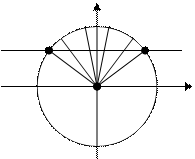 х1 0 х2 y n
х1 0 х2 y n
.
 sin x > a – решением данного неравенства является B A y=a
sin x > a – решением данного неравенства является B A y=a
множество углов, синусы которых превышают значение а. Pp-arcsin a Parcsin a
Это множество углов опирается на дугу АnВ (А= Parcsin a, o x
В = Pp-arcsin a)
Строгое (нестрогое) неравенство не включает (включает)
в решение границы рассматриваемого промежутка из области
определения аргумента.
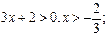 xÎ(-2/3;¥)– решением неравенства явл. интервал, т.е.множество решений
xÎ(-2/3;¥)– решением неравенства явл. интервал, т.е.множество решений
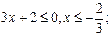 xÎ(-¥;-2/3].
xÎ(-¥;-2/3].
О: Неравенство называется тригонометрическим, если оно содержит переменную только под знаком тригонометрической функции
Решить тригонометрическое неравенство значит найти множество значений переменной, при которых неравенство выполняется..
Решение тригонометрических неравенств сводится к решению простейших неравенств типа:
sin x < a, sin x > a, cos x < a, cos x > a, tg x < a, tg x > a, ctg x < a, ctg x > a
sin x £ a, sin x ³ a, cos x £ a, cos x ³ a, tg x £ a, tg x ³ a, ctg x £ a, ctg x ³ a.
Алгоритм решения тригонометрического неравенства:
1) строим тригонометрический круг;
2) находим концы дуги, на которую будет опираться множество искомых улов (решений) через соответствующую arc функцию числа а;
3) записываем решение неравенства в общем виде: 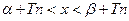 , где α, β – концы дуги, Tn – периоды соответствующих функций.
, где α, β – концы дуги, Tn – периоды соответствующих функций.



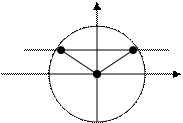 Пример:
Пример: 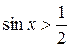 - решением данного неравенства является множество углов больших
- решением данного неравенства является множество углов больших 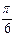 , но меньших
, но меньших 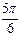 у =1/2
у =1/2 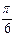
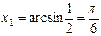
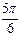 о х
о х

Это множество углов определяет дугу окружности, лежащую выше прямой 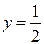
Вывод решения неравенства 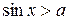 , | а | £ 1, a > 1 – решений нет,
, | а | £ 1, a > 1 – решений нет,
если а < - 1, то решением является множество R
Воспользуемся алгоритмом:
 у
у
 1) n
1) n

 А у = а В
А у = а В
 p-a a
p-a a
 о х
о х
-(p+a)
m
2) ищем концы дуги, на которую опирается множество всех углов, синусы которых больше значения а т.е. из sin x = a, x1 = arcsin a=α и х2 =p - α
Этому множеству углов соответствует дуга AnB, расположенная выше прямой у = а, концы её не входят в решение, т.к. неравенство строгое!
|
3) где 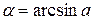 (верхняя дуга)
(верхняя дуга)
Неравенству 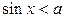 аналогично соответствует нижняя дуга AmB: (нижняя дуга)
аналогично соответствует нижняя дуга AmB: (нижняя дуга)
|
 Пример1:
Пример1: 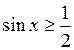


 1) у у=1/2 2) концы дуги:
1) у у=1/2 2) концы дуги: 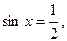
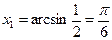 ,
, 


 0 х 3)
0 х 3) 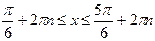 ,
, 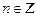 - общее решение
- общее решение
Ответ:[ 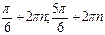 ],
], 
у

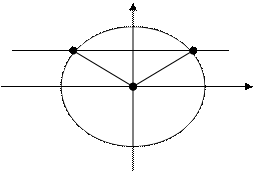 Пример 2:
Пример 2: 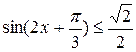 -5p/4 у=
-5p/4 у= 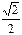 p/4
p/4
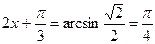
 о х
о х
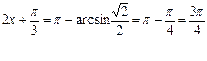
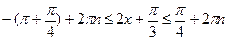
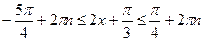 (вычитаем из всех частей неравенства вел.
(вычитаем из всех частей неравенства вел. 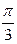 )
)
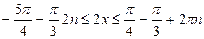
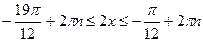 (делим все части неравенства на 2)
(делим все части неравенства на 2)
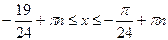
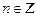 Ответ:[
Ответ:[ 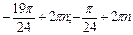 ],
], 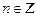
Рассмотрим 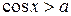 ,
, 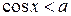 , |
, | 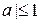 , a > 1 – решений нет,
, a > 1 – решений нет,
если 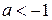 - решение вся R
- решение вся R
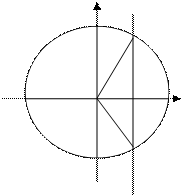
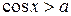 - решением является множество углов, косинусы которых больше значения а, т.е. дуга (концы не входят, т.к. неравенство строгое), лежащая правее прямой х = а
- решением является множество углов, косинусы которых больше значения а, т.е. дуга (концы не входят, т.к. неравенство строгое), лежащая правее прямой х = а

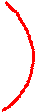
 у х = а Проводим рассуждения как и в предыдущем случае, имеем:
у х = а Проводим рассуждения как и в предыдущем случае, имеем:
Рarccos a 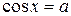
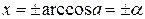
о х
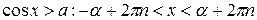
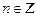 (дуга справа)
(дуга справа)
 |
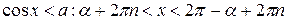
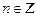 (дуга слева)
(дуга слева)
P-arccos a

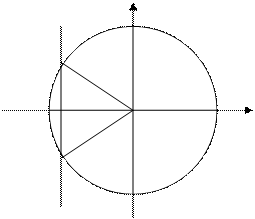 Пример 4:
Пример 4: 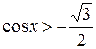 х = -
х = - 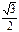 у
у
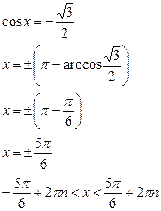
 5p/6
5p/6
о х
 -5p/6
-5p/6

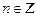 Ответ: (
Ответ: (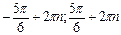 ),
), 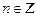
y





 Рассмотрим
Рассмотрим 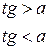
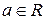 y = a
y = a
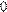

 Построим графики
Построим графики 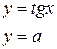 и найдем точки пересечения
и найдем точки пересечения


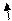

 данных графиков -p/2 о p/2
данных графиков -p/2 о p/2
a =arctg a
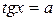 ,
, 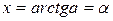
Учитывая область определения функции у=tg x, для строгих и нестрогих неравенств получим следующие общие формулы решений:
1) 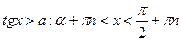 2)
2) 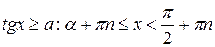
3) 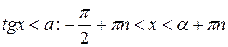 4)
4) 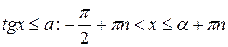 -
- 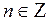
Пример 4: 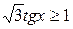 ,
,
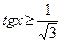 ,
, 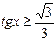 ,
, 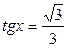 ,
, 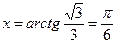 ,
, 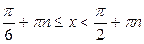 ,
, 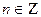
Аналогично решаются неравенства, содержащие функцию ctg x, т.е. 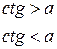 ,
, 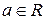
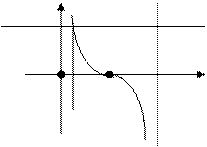
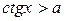 , у
, у
Находим концы дуги через 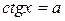 y = a
y = a
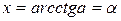

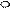

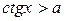
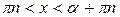 (выше прямой у = а) о p/2 p х
(выше прямой у = а) о p/2 p х


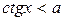
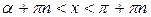 (ниже прямой у = а) a=arcctg a
(ниже прямой у = а) a=arcctg a
Учитывая область определения функции у = ctg x, для нестрогих неравенств получим следующие общие формулы решений:
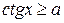
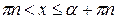
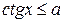
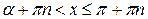 ,
, 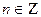
Пример 5: 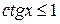 ;
; 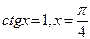 ;
; 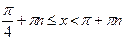
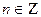
Пример 6: 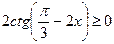 ;
; 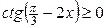 ;
; 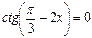 ;
; 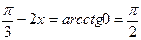
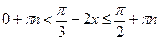 ;
; 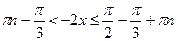 ;
; 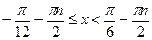 ;
;
Ответ: 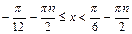 ,
, 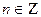
Выводы:
1) 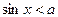
| 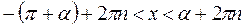
| a-значение соответствующего аркуса | |
2) 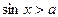
| 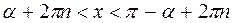
| ||
3) 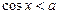 , ,
| 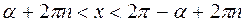
| ||
4) 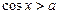
| 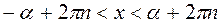
| ||
5) 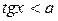
| - 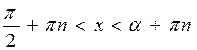
| 5) 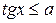
| - 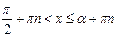
|
6) 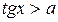
| 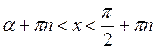
| 6) 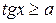
| 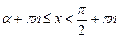
|
7) 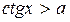
| 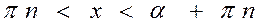
| 7) 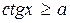
| 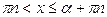
|
8) 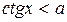
| 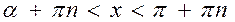
| 8) 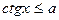
| 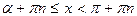
|
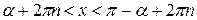 ,
,