Определение 6 (предел функции в бесконечности).

Предел функции.

Определения и примеры.

Пусть EÌ R и a – предельная точка множества E.

Определение 1. Будем говорить, что a –предельная точка для множества E, если любая окрестность точки a содержит бесконечное подмножество множества E.

Пусть f:E ® R. Приведем несколько формулировок определения предела функции. Для разных оценок бывает удобна то одна, то другая.

Определение 2 (предел функции по Коши). Число A Î R называется пределом функции f(x) в точке a или при x® a и это обозначается следующим образом lim _x ® af (x) = A, если

" e > 0 $ d(e)>0: " x: 0 <|x-a|< d, Þ |f (x) -A|< e

Пример 1. Доказать, что lim_{x® 1}(2x+3) = 5.

Запишем определение предела для данного примера

" e >0 $ d (e)>0 " x удовлетворяющих условию: 0 <|x- 1 |< d

должно быть выполнено неравенство

| 2 x+ 3-5 |< e или 2 |x- 1 |< e.

Отсюда следует, что неравенство 2|x-1|<2d<e выполнится, если d£e/2. Если e = 0,1, то d = 0,05, при e = 0,01, d = 0,005 и т.д. Таким образом, решение задачи состоит в нахождении d, зависящего от e.

Определение 3. Проколотой окрестностью точки называется окрестность точки, из которой исключена эта точка.

Обозначается проколотая окрестность символом .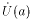

Определение 4 (предел функции на "языке окрестностей"). Число A Î R называется пределом функции f(x) в точке a или при x® a,
если для любой окрестности U (A) числа A существует проколотая окрестность 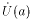точки a такая, что f (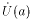) Ì U (A).

Приведем еще одно эквивалентное определение предела на "языке последовательностей".

Определение 5 (предел функции по Гейне). A=lim_{x ® a}f(x)
означает, что

" x_n ® a при n ® ¥; x_n ¹ a, f (x_n) ® A при n ® ¥

Пример 2. Покажем, что не существует предела f(x) = sin(1/x) при x® 0. Для этого используем определение предела на языке последовательностей. Выберем две последовательности x_n1 = 1/p n, x_n2 = 1/(p/2+2p n), которые обе сходятся к нулю при n®¥. Тогда sin x_n1 = sin p n=0, sin x_n2 = sin (p/2+2p n) = 1, Таким образом, f(x_n1) и f(x_n2) сходятся к разным числам, поэтому определение предела на "языке последовательностей" не выполняется.

Пример 3. Рассмотрим функцию Дирихле

, где Q – множество рациональных чисел, соответственно множество R\ Q – множество иррациональных чисел. Данная функция не имеет предела ни в одной точке a действительной прямой. Действительно, если выбрать последовательность рациональных чисел, сходящихся к a, то соответствующая последовательность значений функции сходится к единице. Если выбрать последовательность иррациональных значений, то значения функции сходятся к нулю. Следовательно, на основании определения предела по Гейне данная функция не имеет предела.

Рассмотрим геометрический смысл предела функции в точке. Неравенство |f(x)-A|<e равносильно двойному A-e<f(x)<A+e. Число A есть предел функции f(x) при x®a, если для любого e >0 найдется такая d -окрестность точки a, что для всех x¹ a из этой окрестности соответствующие значения функции f(x) будут заключены в полосе A-e<f(x)<A+e (см. рис. 14).

Рассмотрим понятие предела функции в бесконечности.

Определение 6 (предел функции в бесконечности).

lim _x ® ¥ f (x) = A,

если

" e > 0 $ B (e) >0: " x таких, что |x| > B, выполняется |f (x) -A| < e

Определение 7.

lim _x ® af (x) = ¥,

если

" A> 0 $ d(A) > 0: " x 0 <|x-a|< d, |f (x) | > A

lim _x ® ¥ f (x) = ¥, если " A> 0 $ B (A)>0: " x |x|> B, |f (x) |> A

Аналогично формулируются определения при x® ±¥, а также определения, когда A = ±¥.

Замечание. Изученное понятие предела последовательности можно рассматривать как частный случай предела функции при x® +¥.

Пример 4. Доказать, что lim _x ® 11 / (x- 1)² = + ¥

" e > 0 $ d(e)>0: " x 0 <|x- 1 |< d выполняется 1 / (x- 1)²> e
1 /|x- 1 | 2>1 / d²> e

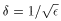
Замечание. Если при стремлении x к a переменная x принимает лишь значения, меньшие a или большие a и при этом f(x) стремится к A, то говорят, что существуют односторонние пределы функции, то есть lim_{x® a-0}f(x) = A – предел слева или lim_{x® a+0}f(x) = A – предел справа. Очевидно, что если lim_{x® a-0}f(x) = lim_{x® a+0}f(x) = A, то lim_{x® a} = A. Верно и обратное утверждение.

Пример 5. Покажем, что не существует предела f(x) = 2^1/x, при x ® 0.
lim _x ® 0-02^{1 /x} = lim _x ® 0-02^{- ¥} = 0
lim _x ® 0+02^{1 /x} = lim _x ® 0+02^{+ ¥} = + ¥

Пределы не равны, следовательно lim _x ® 0 2^{1 /x} не существует.