Взаимное расположение прямой и окружности
Вспомним случаи взаимного расположения прямой и окружности.
Задана окружность с центром О и радиусом r. Прямая Р, расстояние от центра до прямой, то есть перпендикуляр ОМ, равна d.
Случай 1 – расстояние от центра окружности до прямой меньше радиуса окружности:
Мы доказали, что в случае, когда расстояние d меньше радиуса окружности r, прямая и окружность имеют только две общие точки (рис. 1).
Рис. 1. Иллюстрация к случаю 1
Случай второй – расстояние от центра окружности до прямой равно радиусу окружности:
Мы доказали, что в данном случае общая точка единственная (рис. 2).
Рис. 2. Иллюстрация к случаю 2
Случай 3 – расстояние от центра окружности до прямой больше радиуса окружности:
Мы доказали, что в данном случае окружность и прямая не имеют общих точек (рис. 3).
Рис. 3. Иллюстрация к случаю 3
На данном уроке нас интересует второй случай, когда прямая и окружность имеют единственную общую точку.
Определение касательной
Определение:
Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности, общая точка называется точкой касания прямой и окружности.
Прямая р – касательная, точка А – точка касания (рис. 4).
Рис. 4. Касательная
Теоремы о касательной и радиусе
Теорема:
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания (рис. 5).
Рис. 5. Иллюстрация к теореме
Доказательство:
От противного – пусть ОА не перпендикулярно прямой р. В таком случае, опустим из точки О перпендикуляр на прямую р, который будет расстоянием от центра окружности до прямой:
Из прямоугольного треугольника 
можем сказать, что гипотенуза ОН меньше катета ОА, то есть 
, прямая и окружность имеют две общие точки, прямая р является секущей. Таким образом, мы получили противоречие, а, значит, теорема доказана.
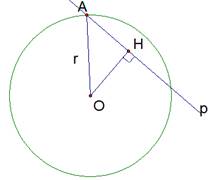
Рис. 6. Иллюстрация к теореме
Справедлива и обратная теорема.
НОВОЕ ЗАПИСАТЬ! Теорема о двух касательных
Теорема:
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна этому радиусу, то она является касательной.
Доказательство:
Поскольку прямая перпендикулярна радиусу, то расстояние ОА – это расстояние от прямой до центра окружности и оно равно радиусу: 
. То есть 
, а в этом случае, как мы ранее доказывали, у прямой и окружности единственная общая точка – это точка А, таким образом, прямая р является касательной к окружности по определению (рис. 7).
Рис. 7. Иллюстрация к теореме
Прямую и обратную теоремы можно объединить следующим образом (рис. 8):
Задана окружность с центром О, прямая р, радиус ОА
Рис. 8. Иллюстрация к теореме
Теорема:
Прямая является касательной к окружности тогда и только тогда, когда радиус, проведенный в точку касания, перпендикулярен ей.
Данная теорема означает, что если прямая является касательной, то радиус, проведенный в точку касания, перпендикулярен ей, и наоборот, из перпендикулярности ОА и р следует, что р – касательная, то есть, прямая и окружность имеют единственную общую точку.
Рассмотрим две касательные, проведенные из одной точки к окружности.
Теорема:
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проведенной через эту точку и центр окружности.
Задана окружность, центр О, точка А вне окружности. Из точки А проведены две касательные, точки В и С – точки касания. Требуется доказать, что 
и что равны углы 3 и 4.
Рис. 9. Иллюстрация к теореме
Доказательство:
Доказательство основано на равенстве треугольников 
. Объясним равенство треугольников. Они являются прямоугольными, так как радиус, проведенный в точку касания, перпендикулярен касательной. Значит, углы 
и 
прямые и равны по 
. Катеты ОВ и ОС равны, так как являются радиусом окружности. Гипотенуза АО – общая.
Таким образом, треугольники равны по равенству катета и гипотенузы. Отсюда очевидно, что катеты АВ и АС также равны. Также углы, лежащие напротив равных сторон, равны, значит, равны углы 
и 
, 
.
Теорема доказана.
Выводы по уроку
Итак, мы познакомились с понятием касательной к окружности, на следующем уроке мы рассмотрим градусную меру дуги окружности.
Домашнее задание
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др., Геометрия 7–9, № 634–637, с. 168.
Четкую фотографию выполненных заданий прислать до 31 марта на адрес:
Https://vk.com/id587584299