Часть 1. Точечные оценки
Задание:
а) Малая выборка
1.Преобразовать выборку в вариационный ряд;
2.Вычислить точечные оценки МО, дисперсии, СКО, коэффициентов вариации, асимметрии и эксцесса;
3.Вычислить точечные оценки медианы и размаха;
4.Построить точечную оценку функции распределения;
5.Рассчитать вероятности случайных событий по полученной функции распределения.
б) Большая выборка
1.Сгруппировать выборку в классы;
2.Составить расчетную таблицу;
3.Найти точечные оценки МО, дисперсии, СКО;
4.Построить гистограмму и полигон относительных частот;
5.Найти Ме, Мо по гистограмме частот;
6.Построить точечную оценку функции распределения;
7.Определить вероятности случайных событий по точечной оценке функции распределения.
Малая выборка представлена на рисунке 1. С помощью функций MATLAB вычисляем математическое ожидание, дисперсию, СКО, медиану коэффициенты вариации, асимметрии, эксцесса, размах. Программа для оценки представлена на рис. 2, полученные результаты на рис. 3.
Строим точечную оценку функцию распределения (рисунок 4). Вычислим вероятности двух случайных событий, например:
1) P(x>9,216)=1-F(9,216)=1-0,400=0,600
2) P(6,793<x<12,237)=F(12,237)-F(6,793)=0,650-0,2=0,450
Рис. 1. Малая выборка
Рис. 2. Программа для оценки характеристик
Рис. 3. Оценка характеристик
Рис. 4. Точечная оценка функции распределения
При помощи hist в MATLAB делим большую выборку (100 чисел) на 10 классов, составляем расчетную таблицу, она представлена на рисунке 5.
При помощи функций Excel определяем точечные оценки математического ожидания, дисперсии, СМО (рис. 6).
Рис. 5. Большая выборка
Рис. 6. Числовые характеристики
Строим гистограмму (рис. 7) и полигон относительных частот (рис. 8)
Находим медиану и моду (рис. 6). Строим оценку функции распределения (рис. 9).
Рис. 7. Гистограмма относительных частот
Рис. 8. Полигон относительных частот
Рис. 9. Функция распределения
Находим вероятности случайных событий, например:
P(x>5,49)=1-F(5,49)=1-0,19=0,81
P(x<7,92)=F(7б92)-0=0,41
Часть 2. Интервальные оценки
Задание:
Малая выборка: построить интервальные оценки для МО при неизвестной дисперсии и для дисперсии с надежностью γ=0,95.
Большая выборка: построить интервальные оценки для МО при известной дисперсии и для дисперсии с надежностью γ=0,95.
Построим интервальную оценку для математического ожидания (n-объем выборки) малой выборки:
Получаем доверительный интервал 
.
Для большой выборки:
Получаем доверительный интервал 
. Значения критерия Стьюдента взяты с сайта kontrolnaya-rabota.ru
Построим интервальную оценку для дисперсии малой выборки:
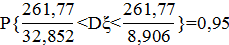
Получаем доверительный интервал 
.
Построим интервальную оценку для дисперсии большой выборки:
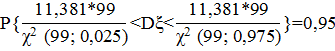
Получаем доверительный интервал 8,7737< 
<15,3588. Значения критерия хи-квадрат определены с помощью функции ХИ2.ОБР.ПХ в Microsoft Excel.
Часть 3. Проверка гипотез
Задание:
1. Малая выборка:
1)Проверка гипотезы о числовом значении МО H0: Mξ=m0 при неизвестной дисперсии.
2)Проверка гипотезы о числовом значении дисперсии H0: Dξ=σ²0
2. Большая выборка:
Проверка гипотезы о числовом значении МО H0: Mξ=m0 при известной дисперсии.
3. Проверка гипотезы о законе распределения.
1)Малая выборка: предложить гипотезу H0 о законе распределения СВ и проверить ее по критерию Колмогорова.
2)Большая выборка: предложить гипотезу H0 о законе распределения СВ и проверить ее по критерию Пирсона.
1) H0: Mξ=m0=9. n=20, 
=10,1935, s2=13,777. Примем α=0,05
Так как 
< 
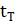, то гипотеза не отвергается
2) H0: Dξ= σ²0 =27. n=20, =10,1935, s2=13,777. Примем α=0,05
= 
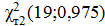=8,9065
= 
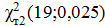=32,85233
Так как 
< 
< 
, гипотеза не противоречит данным выборки.
3) H0: Mξ=m0=9. n=100, =8,975, s2=11,38122. Примем α=0,05
Так как < 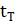, то гипотеза не отвергается.
4) Предположим, что случайная величина, заданная малой выборкой, рас- пределена по нормальному закону с параметрами (10,1935; 3,771). При помощи функции НОРМРАСП в Excel вычислим значения гипотетической функции распределения (рис. 10). Вычислим разность между эмпирической и гипотетической ФР (рис. 10, столбец D)
Рис. 10. Проверка гипотезы о законе распределения
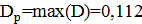
Разность меньше, чем предельно допустимая, значит гипотеза не отвергается.
5) Предположим, что случайная величина распределена по нормальному закону с параметрами (8,975; 3,37). Разделим выборку на 7 классов. Вычислим критерий 
(рис. 11).
Критерий хи2 получился меньше табличного, значит гипотеза о нормальном распределении выборки не противоречит исходным данным.
Рис. 11. Проверка гипотезы о законе распределения
Выводы: были произведены расчеты характеристик случайных величин, изучены методы построения интервальных оценок и проверки гипотез.