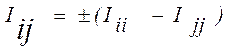Метод непосредственного применения законов Кирхгофа

Старооскольский технологический институт

(филиал)

Московского государственного института

Стали и сплавов

(технологического университета)

Рекомендовано

Методическим советом

СТИ МИСиС

Боева Л.М.

Теоретическая электротехника

Методические указания

К выполнению домашнего задания №1

Для студентов заочного отделения специальности

Автоматизация технологических процессов и производств»

Старый Оскол

 

 

Рецензент:

Директор ЗАО «Проектэлектромонтаж» Пожарский Ю.М.

 

Составитель:

Боева Л.М.

 

Методические указания к выполнению домашнего задания №1 по курсу «Теоретическая электротехника», для студентов заочного отделения специальности 210200 «Автоматизация технологических процессов и производств»

 

 

© Боева Л.М.

 

СОДЕРЖАНИЕ

 

Введение. 4

1 Требования к оформлению домашнего задания. 4

2 Основные теоретические положения. 5

2.1 Преобразование треугольника сопротивлений в звезду и обратно. 5

2.2 Метод непосредственного применения законов Кирхгофа. 5

2.3 Метод контурных токов. 6

2.4 Метод узловых потенциалов. 6

2.5 Метод наложения токов. 7

2.6 Метод эквивалентного генератора. 8

2.7 Метод узлового напряжения. 8

2.8 Потенциальная диаграмма. 9

2.9 Баланс мощности электрической цепи. 9

3 Пример расчета. 10

4 Задание для выполнения. 25

5 Список литературы.. 27

 

 

Введение

Предмет «Теоретическая электротехника» является одной из базовых дисциплин при подготовке инженеров по автоматизации технологических процессов и производств. В ходе его изучения рассматриваются, в частности, основы теории линейных цепей постоянного тока. В процессе освоения курса ТЭ решающее значение имеет не только накопление теоретических знаний по специальности, но и практическое овладение основными методами расчета. Одной из форм самостоятельной работы студентов является выполнение индивидуальных домашних заданий по разделу «Расчет сложных электрических цепей постоянного тока».

Настоящие методические указания включают в себя основные теоретические положения по теме задания, варианты задания, методические рекомендации по его выполнению, примеры расчета.

 

Требования к оформлению домашнего задания

ДЗ оформляется на отдельных листах формата А4. Задание должно содержать:

- номер варианта задания;

- формулировку и условия задач;

- расчетные формулы и необходимые пояснения.

Физические величины следует приводить в системе СИ.

Результаты однотипных расчетов, многократно выполняемых по одним и тем же формулам, следует сводить в таблицу.

Графики следует выполнять на миллиметровой бумаге с указанием масштаба и единиц измерения.

Если ДЗ выполнено правильно и в срок, оно засчитывается без индивидуального собеседования. ДЗ с ошибками возвращается студенту на доработку. После доработки ДЗ засчитывается после индивидуального собеседования с преподавателем.

 

Основные теоретические положения

Преобразование треугольника сопротивлений в звезду и обратно

Преобразование треугольника сопротивлений R₁₂, R₂₃, R₃₁ в звезду сопротивлений R₁,R₂,R₃ и обратно производится при условии, что потенциалы узловых точек 1, 2, 3, являющихся вершинами треугольника и эквивалентной звезды, не меняются (рис.1).

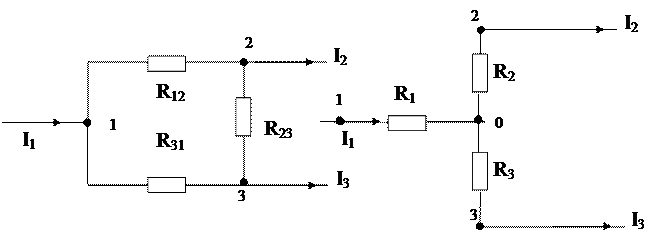
Рис.1 - Преобразование треугольника сопротивлений в звезду и обратно

 

Сопротивления звезды рассчитаны по формулам:

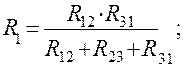
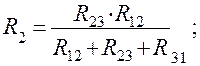
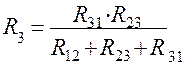
Сопротивления треугольника рассчитаны по формулам:

; ;

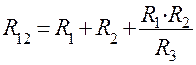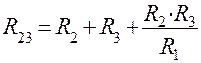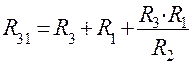
Метод непосредственного применения законов Кирхгофа

1.Определяется число узлов схемы n и число ветвейв схеме m.

2.Произвольно выбирается направление токов во всех ветвях и направление обхода (m-n+1) контуров.

3.Составляется система из m уравнений, где (n-1) уравнений составляются по I закону Кирхгофа, и (m-n+1) уравнений - по II закону Кирхгофа.

4.Решается система m линейных уравнений, из которой определяются токи в ветвях.

Метод контурных токов

Позволяет сократить число уравнений системы до (m-n+1).

1.Определяется число узловсхемы n и число ветвей в схеме m.

2.Произвольно выбирается направление токов во всех ветвях и одинаковое (по часовой стрелке или против часовой стрелки) направление обхода (m-n+1) контуров.

3.Задаются контурные токи 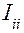как собственные токи каждого независимого контура схемы. Их направление совпадает с выбранным направлением обхода контура.

4.Вычисляются:

- контурные э.д.с. 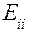как алгебраическая сумма входящих в контур э.д.с. источников;

- собственные сопротивления 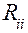контуров как сумма всех входящих в контур сопротивлений;

- общие сопротивления 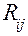контуров как сумма сопротивлений двух смежных контуров.

5.Составляется система из (m-n+1) уравнений по II закону Кирхгофа, в которых справа – контурные э.д.с., а слева – сумма падений напряжения, созданного контурным током своего контура на собственном сопротивлении контуров (со знаком «+») и созданных контурными токами смежных контуров на общих сопротивлениях контуров (со знаком «-»).

6.Решается система (m-n+1) линейных уравнений, из которых определяются контурные токи.

7.Определяются токи в ветвях через контурные токи. В ветвях, общих для смежных контуров, токи равны алгебраической сумме соответствующих контурных токов: