Фильтры электрических сигналов

7.1. Основные понятия и определения

В современных многоканальных системах связи широко используется частотный принцип разделения сигналов. Он состоит в том, что каждому сигналу отводится своя полоса частот. Важнейшую роль при обработке таких сигналов играют фильтры электрических сигналов.

Фильтры – это устройства, которые предназначены для пропускания сигналов в определенной полосе частот и подавления сигналов за пределами этой полосы частот. Обычно фильтр – это четырехполюсник (рис. 7.1.).

Передача сигнала через фильтр характеризуется двумя способами.

1) Комплексным коэффициентом передачи по напряжению:

K_u (j w) = U _{2 m} / U _{1 m}

или его амплитудно-частотной характеристикой(АЧХ):

K_u (w) = | U _{2 m} / U _{1 m} |.

Коэффициент передачи – это относительная безразмерная величина. Иногда его характеризуют относительной логарифмической величиной K_u [дБ] = 20 lg K_u, ее размерностью является децибел (дБ). Коэффициент передачи показывает, какая доля входного сигнала проходит через фильтр.

2) Коэффициентом затухания по напряжению:

a(j ω) = U _{1 m} / U _{2 m} = 1/ K_u (j w); a(ω) = | U _{1 m} / U _{2 m} |, a[дБ] = –20 lg K_u (w).

Он показывает долю сигнала, которая затухает, проходя через фильтр.

Избирательные свойства фильтра тем лучше, чем ближе форма АЧХ к прямоугольной. Идеальный фильтр имеет прямоугольную АЧХ.

3) Полоса пропускания (ПП) идеального фильтра – это диапазон частот, в котором K (ω) = 1, a = 1.

4) Полоса задержания, или заграждения (ПЗ), – это диапазон частот, в котором K (ω) = 0, a®¥.

5) Частота, являющаяся границей между полосой пропускания и полосой задержания, называется граничной частотой, или частотой среза (f _гр или f _ср).

У реальных фильтров нет четкой границы между ПП и ПЗ, поэтому в них за значение граничной частоты f _гр принимают частоту, определяемую из соотношения ≈ 0,707.

Скорость спада АЧХ коэффициента передачи K_u в полосе заграждения рассчитывается из выражения

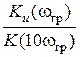V = – 20 lg Þ .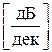

Его скорость спада идеального фильтра бесконечна.

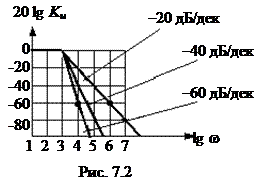
На рис. 7.2. изображены амплитудно-частотные характеристики фильтра низких частот (ФНЧ) в логарифмическом масштабе при разных скоростях спада.

 

7.2. Классификация фильтров электрических сигналов

1) В зависимости от характера входного сигнала фильтры делятся:

- на аналоговые,

- цифровые.

2) В зависимости от наличия в схеме активных элементов:

– пассивные, состоящие только из пассивных элементов,

–активные – устройства, содержащие усилительные элементы и пассивные фильтры.

3) В зависимости от элементов, составляющих фильтр:

– LC-, RC-, и RL -типа,

– АRC -типа (активные RC- фильтры).

4) По характеру математического выражения аппроксимирующего АЧХ фильтра:

– фильтры Бесселя, Баттерворта, Золотарева, Чебышева и др.

5) По расположению полосы пропускания на оси частот фильтры делятся:

– на фильтры низких частот (ФНЧ). Их АЧХ коэффициента передачи приведена на рис. 7.3 а. АЧХ идеального фильтра имеет прямоугольный характер, а у реального нет четкой границы между полосой пропускания и полосой заграждения.

– Фильтры высоких частот (ФВЧ). Их АЧХ коэффициента передачи приведена на рис.7.3 б:

– Полосно-пропускающие фильтры (ППФ). Их АЧХ коэффициента передачи приведена на рис. 7.3 в, где ω₀ – средняя частота полосы пропускания;
ω_в.гр, ω_н.гр – соответственно верхняя и нижняя граничные частоты полосы пропускания. Если ω₀/(ω_в.гр–ω_н.гр) >> 1, то фильтры называют избирательными, такие фильтры пропускают сигналы в узком диапазоне частот.

– Полосно-заграждающие фильтры (ПЗФ). Их АЧХ коэффициента передачи приведена на рис. 7.3 в, где ω₀ – средняя частота полосы задержания; ω_в.гр, ω_н.гр – соответственно верхняя и нижняя граничные частоты полосы задержания. Если ω₀/(ω_в.гр – ω_н.гр) >>1, то фильтры называют режекторными, они подавляют сигнал в узком диапазоне частот.

а б в г
Рис. 7.3

7.3. Схемы электрических фильтров

Основой для построения фильтров является каскадное (последовательное) соединение Г-, Т- или П-образных четырехполюсников (рис. 7.4). Каждый из четырехполюсников в теории фильтров называют звеном фильтра.

 

U 2 m

U 1 m

Um+ 1

K 1

K 2

Ku

Рис. 7.4

Если звенья фильтров удовлетворяют условию R _вых<< R _вх, то такие звенья можно считать независимыми, так как они не влияют на коэффициент передачи по напряжению друг на друга. В этом случае общий коэффициент передачи фильтра K_{u общ} можно записать как произведение коэффициентов передач K_ui отдельных звеньев, входящих в фильтр

.

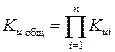7.3.1. Схемы звеньев фильтров

Избирательные свойства звеньев фильтра и фильтра в целом объясняются тем, что в их схему входят элементы (катушки индуктивности и емкости), сопротивления которых зависят от частоты.

Для простейшей Г-образной схемы с комплексными сопротивлениями Z ₁ и Z ₂ коэффициент передачи по напряжению определяется выражением

.

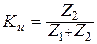Отсюда следует, что на частотах, когда | Z ₂|>>| Z ₁|, K_u » 1 – это полоса пропускания. На тех частотах, когда | Z ₂|<<| Z ₁|, K_u » 0 – это полоса заграждения.

Рассмотрим конкретные схемы звеньев фильтра.

1) Простейшие схемы однозвенных ФНЧ приведены на рис. 7.5.

На рис. 7.5 а, б и в приведены Г-образные схемы соответственно RC -типа, RL -типа и LC -типа типа, а на рис. 7.5, г, д приведены Т- и П-образные схемы на L C-элементах. Работа, например, фильтра RC -типа происходит следующим образом. Если ω→0, то сопротивление конденсатора (1/ω С)→∞, а следовательно, U _{2 m} = U _{1 m}, т.е. сигнал передается через цепь без ослабления. При увеличении частоты входного сигнала сопротивление конденсатора уменьшается, (1/ω С)→0. Амплитуда выходного напряжения на конденсаторе | U _{2 m} |→0 и, следовательно, высокочастотный сигнал через фильтр не проходит, т.е. подавляется.

 

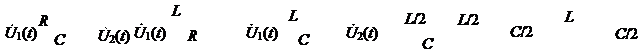
а б в г д
Рис. 7.5

Комплексный коэффициент передачи по напряжению K_u (j w) = U _{2 m} / U _{1 m} и амплитудно-частотная характеристика(АЧХ) K_u (w) = | U _{2 m} / U _{1 m} | рассмотренного ФНЧ определяются из выражений:

K_u (j ω) = (1+ j ω R C)^–1, K_u (ω) = (1+(ω R C)²)^–1/2.

Фильтр с одним реактивным элементом называется фильтром первого порядка, поскольку он описывается дифференциальным уравнением 1-го порядка. Скорость его спада составляет 20 дБ на декаду. Фильтр с двумя реактивными элементами (рис. 7.5 в) является фильтром второго порядка. Его коэффициент передачи является вещественным числом: K_u (j w) =[1-(w LC)²]^-1 и скорость спада составляет 40 дБ на декаду.

2) Простейшие схемы однозвенных ФВЧ приведены на рис. 7.6.

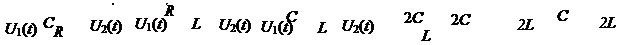
а б в г д

Рис. 7.6

На рис. 7.6 а–в приведены Г-образные схемы соответственно RC -типа, RL -типа и LC -типа, а на рис.7.6 г, д приведены схемы Т- и П-образные схемы на LC -элементах. Работа, например, фильтра RC -типа, происходит следующим образом. Если ω → 0, то сопротивление конденсатора (1/ω С) → ∞, а следовательно, U _{2 m} → 0, – низкочастотный сигнал через фильтр не проходит, т.е. подавляется. При увеличении частоты входного сигнала сопротивление конденсатора уменьшается (1/ω С)→0, следовательно, U _{2 m} = U _{1 m}, т.е. высокочастотный сигнал передается через цепь без ослабления.

3) Полосно-пропускающий фильтр можно получить путем последовательного соединения двух звеньев ФНЧ и ФВЧ, подобрав соответствующим образом их граничные частоты. Однако на практике часто используют схему моста Вина (рис. 7.7 а). На рис.7.7 б приведена зависимость его коэффициента передачи от частоты. На рис.7.7 в приведена схема ППФ на основе последовательного контура.

w0 = (RC)–1

w

1/3

ФНЧ

ФВЧ

Ku

R

R

C

C

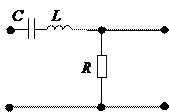
а б в
Рис. 7.7

4) Полосно-заграждающий фильтр (ПЗФ) можно получить путем последовательного соединения ФНЧ и ФВЧ при соответствующем выборе граничных частот.

Однако на практике часто используют схему двойного Т-образного моста (рис. 7.8, а). Зависимость коэффициента передачи от частоты этой схемы приведена на рис. 7.8, б. Аналогичной характеристикой обладает схема на основе последовательного контура (рис. 7.8, в).

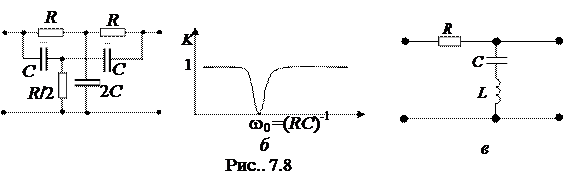7.3.2. Влияние числа звеньев фильтра на его характеристики

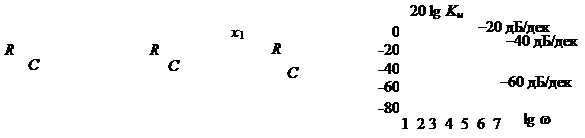Рассмотрим это влияние на сравнении одно- и двухзвенного ФНЧ на
RC -элементах (рис. 7.9, а, б). Будем считать, что в состав второй схемы (рис. 7.9, б) между звеньями входит устройство согласования звеньев по сопротивлениям. Согласующий каскад [ x ₁] имеет большое входное (R _вх ® ¥) и малое выходное (R _вых ® 0) сопротивления, при этом его коэффициент передачи равен единице (К_u =1). Э то позволяет считать 1-е и 2-е звено независимыми.

а б в

Рис.7.9

Для первой схемы комплексный коэффициент передачи по напряжению и его АЧХ определяются из выражений:

; .

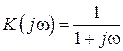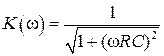Граничная частота звена определяется из соотношения w_гр = 1/(R C). В полосе заграждения при w > w_гр коэффициент передачи убывает со скоростью K_u (w) ~ 1/w, т.е. при увеличении w в 10 раз K_u (w) убывает в 10 раз. Это убывание в логарифмических единицах составляет величину 20 дБ на декаду, т.е.
v = –20 дБ/дек.

Фильтр с одним реактивным элементом называется фильтром первого порядка, поскольку он описывается дифференциальным уравнением 1-го порядка.

Рассмотрим АЧХ комплексного коэффициента передачи по напряжению для двухзвенного фильтра. Она определяется как произведение коэффициентов передач звеньев

K_u (w) = K ₁ K ₂= .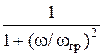

При w > ω_гр K_u (w)~1/w², т.е. v = – 40 дБ/дек.

Вывод. Чем больше звеньев в фильтре, тем выше скорость спада в полосе заграждения (v) и тем фильтр ближе к идеальному. При независимых звеньях скорость спада составляет v = n 20 дБ/дек, где n – число звеньев.

 

 

Контрольные вопросы

1. Для чего предназначены фильтры электрических сигналов?

2. Какими основными параметрами описываются фильтры электрических сигналов?

3. Как классифицируются фильтры электрических сигналов?

4. Охарактеризуйте основные схемы построения электрических фильтров?

5. Как влияет число звеньев фильтра на его характеристики?

6. Как определяется полоса пропускания фильтра?

7. Как называется диапазон частот, в котором коэффициент передачи по напряжению и коэффициент затухания в идеальных фильтрах равны единице?

8. Что собой представляет частота среза фильтра?

9. Как рассчитывается комплексный коэффициент передачи N -звенного фильтра, если звенья одинаковы, обладают комплексным коэффициентом передачи Ki (j ω) и согласованы по напряжениям.

10. Какова временная диаграмма сигнала на выходе ФНЧ при подаче на вход последовательности прямоугольных импульсов (рис. 7.10)?

.

а б в г
Рис. 7.10

11. Какова временная диаграмма сигнала на выходе ФВЧ при подаче на вход последовательности прямоугольных импульсов (рис. 7.10)