Методика введения понятия «иррациональное число»

Существует три подхода к введению понятия «иррациональное число».

I. При первом подходе можно выделить три основных этапа введения понятия: мотивационный, введение понятия, первичное закрепление.

1. Мотивационный этап. На этом этапе можно предложить решить следующую задачу: «Найти сторону квадрата, площадь которого равна 2». Алгебраической моделью ситуации является уравнение 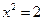. Решением этого уравнения (с учетом того, что длина выражается положительным числом) является арифметический квадратный корень из 2. Это число. Встает вопрос: «Какому числовому множеству принадлежит это число?»

2. Этап введения понятия. Проиллюстрировать этот этап можно, выполнив лабораторную работу.

Примеры.

1) Является ли 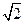целым числом?

Ответ. Рассмотрим квадраты последовательных натуральных чисел: 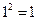, 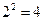. 1 < 2 < 4.

Вывод. Среди целых чисел значения 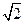нет.

2) Является ли 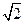рациональным числом?

Ответ. Рассмотрим приближенные значения 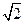с точностью до 0,01; 0,001 и т.д.

1,1² = 1,21

1,2² = 1,44

1,3² = 1,69

1,4² = 1,96

1,5² = 2,25

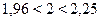, тогда .

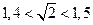Выполняя аналогичную работу на отрезке 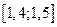, получим:

.

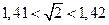Увеличивая точность приближения, можно показать: 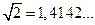. Уже на этом этапе можно увидеть, что 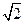– бесконечная непериодическая дробь.

С использованием микрокалькулятора получим: 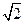= 1,4142135623….

Вывод (предположение) на этом этапе. 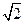– не рациональное число.

3) Приведите строгое математическое доказательство предположения, сформулированного на предыдущем этапе.

Утверждение. Не существует рационального числа, квадрат которого равен двум. Далее приводится доказательство. (Перед доказательством должна быть проведена подготовительная работа).

4) Существует ли число ?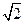

Ответ. Решим исходное уравнение графически.

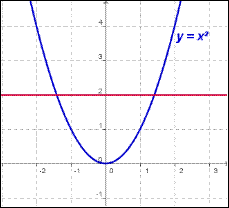
Как видно из рисунка, существует положительное значение абсциссы точки пересечения графиков. Значит, существует число 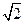. А это, в свою очередь, требует расширения числового множества.

5) Дайте определение иррационального числа.

Ответ. Числа, представляемые бесконечными десятичными непериодическими дробями, называются иррациональными.

Далее приводятся примеры иррациональных чисел: 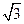; ; 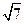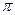и т.д.

Введение понятия «иррациональное число» завершается расширением множества рациональных чисел до множества действительных чисел, структуру которого можно изобразить с помощью кругов Эйлера (швейцарский математик 1707-1773).

3. Этап первичного закрепления. На этом этапе целесообразно решать задачи на установление взаимосвязи известных числовых множеств, сравнение чисел, изображение чисел точками координатной прямой.

II. При втором подходе к ведению понятия «иррациональное число» («Алгебра–8» под ред. С.А. Теляковского) можно предложить ученикам следующие задания.

Примеры. 1) Найдите длину отрезка 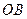при выбранной единице измерения .

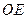Эта задача иллюстрирует, что процесс измерения может быть бесконечным, а отрезки несоизмеримыми.

2) Вычислите длины отрезка, если он составляет 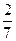единичного отрезка.

Ответ. .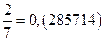

3) Приведите геометрическое доказательство того, что отношение площади квадрата, построенного на диагонали данного квадрата, к площади данного равно 2.

Ответ. Длина диагонали квадрата равна числу, квадрат которого равен 2; при измерении длины диагонали (при условии, что единица измерения – длина стороны данного квадрата) получается бесконечная непериодическая десятичная дробь.

4) Приведите строгое доказательство, что не существует рационального числа, квадрат которого равен двум.

5) Дайте определение иррационального числа.

6) Постройте множество действительных чисел.

III. При третьем подходе к введению понятия (Ш.А. Алимов и др. «Алгебра–8») можно привести формулировку определения и проиллюстрировать его примерами.

Методика введения понятия «комплекс­ное число»

При первом подходе к введению понятия «комплекс­ное число» можно воспользоваться следующей методикой.

1. Устанавливается взаимно однозначное соответствие меж­ду множеством действительных чисел и множеством точек числовой прямой. Утверждается (с привлечением теории гео­метрии), что существует взаимно однозначное соответствие между парами чисел и точками координат­ной плоскости. И как следствие: каждую пару действительных чисел, записанных в определенном порядке, логично рассматривать как некоторое новое число, изображаемое некоторой точкой координат­ной плоскости.

Определение. Пара действительных чисел, заданных в определенном порядке, называется комплексным числом.

2. Выделяется подмножество 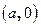изображаемое точками оси абсцисс, которое является геометрическим образом множества действительных чисел. Устанавливается соответствие между множеством действительных чисел и множеством комплексных чисел. Комплексное число вида 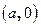– действительное число.

Определение. Комплексное число вида , где , называется мнимым числом.

Комплексное число вида 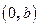, где , называется чис­то мнимым числом.

Для числа вида вводятся понятия: (а) – действительная часть комплексного числа, (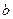) – мнимая часть комплексного числа.

Далее определяются действия на множестве комплексных чисел, заданных парами. И только затем вводится мнимая единица, алгебраическая и тригонометрическая формы записи ­комплексного числа и правила выполнения действий с учето­м формы записи.

При подходе Ш.А. Алимова к введению понятия «компле­ксного числа» рекомендуется следующая методика работы.

1. Мотивационный момент: нахождение корней уравнения 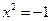; введение i как значения квадратного корня из – 1.

Определение. Комплексными числами называют выра­жения вида 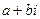, где а и 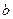– действительные числа, а i – не­который символ такой, что .

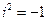2. Здесь же определяются сопутствующие понятия: дейст­вительная и мнимая части комплексного числа.

3. Далее вводятся действия с комплексными числами в алге­браической форме, дается геометрическая интерпретация комплексного числа, тригонометрическая форма записи и действия с комплексными числами в тригонометрической форме записи.

Н.Я. Виленкин предлагает другой подход к введению поня­тия «комплексного числа». Он дает определение комплексного числа (вариант первого подхода). Далее сразу вводится мнимая ­единица, алгебраическая форма записи и действия в алгебраич­еской форме записи и т.д. в той же последовательности, что в подходе Ш.А. Алимова.

Выводы.

Расширение числовых систем осуществляют с учетом принципа перманентности. В учебниках математики реализуются различные последовательности расширения множества натуральных чисел до множества рациональных чисел.

Иррациональные числа отражают несоизмеримость отрезков. Пополнение рациональных чисел иррациональными приводит к непрерывному множеству действительных чисел.

Комплексные числа можно вводить на основе разного сочетан­ия алгебраического и геометрического подходов.