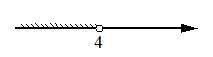Промежуточная контрольная работа.

Тема: Промежуточная контрольная работа по математике 9 класс

ФИО педагога: Чайдонов Владимир Александрович

Место работы: МБОУ КСОШ

Должность: Учитель

Класс: 9

 

Цель: установление фактического уровня теоретических знаний обучающихся по математике и достижения результатов освоения образовательной программы, их практических умений и навыков по ключевым темам программы; оценка достижений конкретного учащегося, позволяющая выявить пробелы в освоении им образовательной программы и учитывать индивидуальные потребности учащегося в осуществлении образовательной деятельности.

Задачи: проверить уровень усвоения обучающимися основных тем программы математики 9 класса и умения применять знания при: действиях с действительными числами и рациональными выражениями; вычислении арифметических квадратных корней; решении линейных неравенства с одной переменной и их систем; действиях со степенями с целыми показателями; решении квадратных уравнений; решении текстовых задач с помощью рациональных уравнений; решении геометрических задач на применение свойств четырехугольников, практических задач на применение теоремы Пифагора.

Данная контрольная работа включает в себя задания по алгебре и геометрии. Задания первой части (1-8) оцениваются по 1 баллу за каждое правильно выполненное задание. В 1 части содержатся задания с выбором ответа (задания 2,8) и с записью краткого решения и ответа (задания 1, 3, 4, 5, 6, 7).

Задания второй части (9-11) оцениваются по 2 балла за каждое правильно выполненное задание. В этих заданиях необходимо указать развернутое решение. Если при выполнении задания второй части допущена вычислительная ошибка, задание может быть оценено 1 баллом.

Время выполнения работы – 45 минут.

Шкала соответствия набранных баллов оценке:
9-14 баллов – высокий уровень обученности
5 - 8 баллов – средний уровень обученности
до 5 баллов – низкий уровень обученности
В работе представлены четыре варианта по 11 заданий и ответы к ним.

 

Промежуточная контрольная работа

1 вариант

Часть 1

Модуль «Алгебра»

1. Найдите значение выражения

0,3 - .

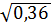Ответ:.

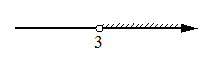
2. Укажите решение системы неравенств

x > − 1,

− 4− x >0.

1)   2)   3)   4) нет решений

3. Найдите значение выражения

(a²)⁵⋅ a⁻⁸ при a =−3

Ответ:.

4. Найдите корни уравнения

x² - 3x - 4 = 0

Ответ:.

5. Выполните действие: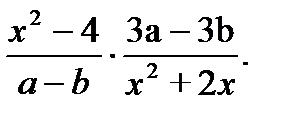

Ответ:.

 

 

Модуль «Геометрия»

6. Най­ди­те боль­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной AB углы, рав­ные 30° и 45° со­от­вет­ствен­но.

Ответ:.

7. По­жар­ную лест­ни­цу при­ста­ви­ли к окну, рас­по­ло­жен­но­му на вы­со­те 15 м от земли. Ниж­ний конец лест­ни­цы от­сто­ит от стены на 8 м. Ка­ко­ва длина лест­ни­цы? Ответ дайте в мет­рах

Ответ:.

8. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Смеж­ные углы равны.

2) Любые две пря­мые имеют ровно одну общую точку.

3) Если угол равен 108°, то вер­ти­каль­ный с ним равен 108°.

Ответ:.

Часть 2

9. (2 балла) Решите неравенство:

10. (2 балла) Пешеход прошел по шоссе 5 км с постоянной скоростью и 6 км по лесу со скоростью на 3 км/ч меньше, чем по шоссе. Найдите скорость пешехода при ходьбе по лесу, если он был в пути 4 часа.

 

11. (2 балла) Боковая сторона равнобокой трапеции равна 5см. Найдите высоту трапеции, если ее основания равны 2см и 8 см.

 

Промежуточная контрольная работа.

2 вариант

Часть 1

Модуль «Алгебра»

1. Найдите значение выражения

2 + ·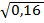

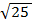Ответ:.

2. Укажите решение системы неравенств x < 3,

4− x > 0.

1)   2)   3)   4)

3. Найдите значение выражения

(х ⁴)²⋅ х ⁻⁶ при х = −2

4. Найдите корни уравнения

5. Выполните действие:

Ответ:.

 

 

Модуль «Геометрия»

6. Най­ди­те угол АDС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной АВ углы, рав­ные 30° и 50° со­от­вет­ствен­но

Ответ:.

 

7. По­жар­ную лест­ни­цу дли­ной 17 м при­ста­ви­ли к окну ше­сто­го этажа дома. Ниж­ний конец лест­ни­цы от­сто­ит от стены на 8 м. На какой вы­со­те рас­по­ло­же­но окно? Ответ дайте в мет­рах

Ответ:.

 

8. Какие из дан­ных утвер­жде­ний верны? За­пи­ши­те их но­ме­ра.

1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой на­крест ле­жа­щие углы равны, то пря­мые па­рал­лель­ны.

2) Диа­го­наль тра­пе­ции делит её на два рав­ных тре­уголь­ни­ка.

3) Если в ромбе один из углов равен 90°, то такой ромб — квад­рат.

Ответ:.

Часть 2

9. (2 балла) Решите неравенство:

10. (2 балла)Из города А в город В, расстояние между которыми 400 км, выехал автобус. Через 1 час вслед за ним выехал легковой автомобиль, скорость которого на 20 км/ч больше, чем скорость автобуса. В город В они прибыли одновременно. Найдите скорость автобуса.

11. (2 балла) В 60 м одна от дру­гой рас­тут две сосны. Вы­со­та одной 31 м, а дру­гой — 6 м. Най­ди­те рас­сто­я­ние (в мет­рах) между их вер­хуш­ка­ми