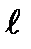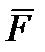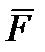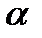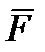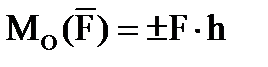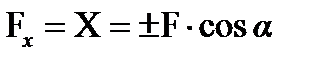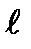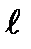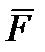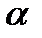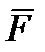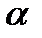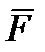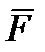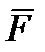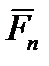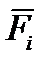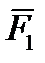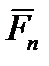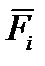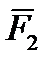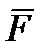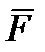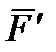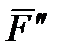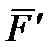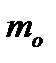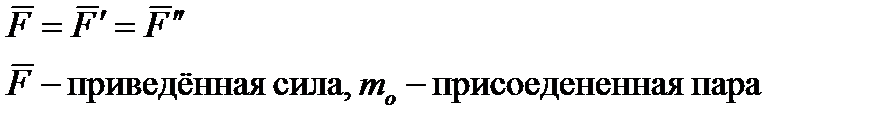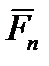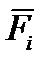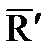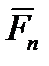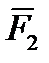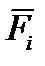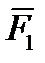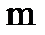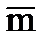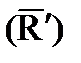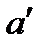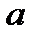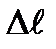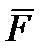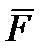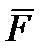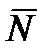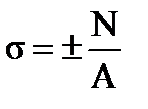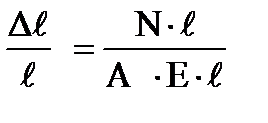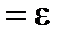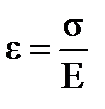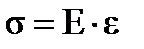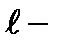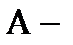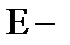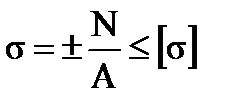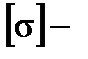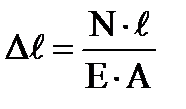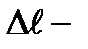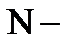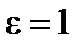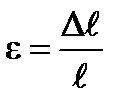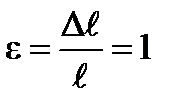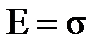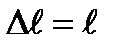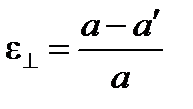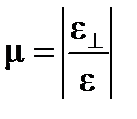Осевое растяжение, сжатие.

Классификация деформируемых тел

В зависимости от соотношения размеров.

1. Массив – тело, у которого все 3 размера (высота, ширина и длина) примерно одного порядка.

L

H

B

 

 

t

2. Пластины и оболочки – тела у которых один размер, значительно меньше двух других.

 

t

 

3. Брус (стержень) – тело, размеры поперечного сечения которого малы, по сравнению с длиной.

B

h

 

 

В курсе сопротивления материалов в основном рассматриваются деформации стержней.

Основные гипотезы и допущения.

Гипотеза о сплошности.

Материал непрерывным образом заполняет объём тела.

Гипотеза об однородности и изотропности.

 

 

Гипотеза об идеальной упругости.

После снятия внешней нагрузки тело полностью восстанавливает свои первоначальные форму и размеры.

В курсе сопротивления материалов рассматриваются только упругие деформации (деформация называется упругой, если она исчезает после удаления вызвавшей её нагрузки).

Гипотеза о малости деформации.

Деформации малы по сравнению с размерами тела.

Гипотеза о пропорциональности деформации внешней нагрузкой (закон Гука).

Деформация пропорциональна внешним нагрузкам.

Гипотеза плоских сечений (гипотеза Бернулли).

Сечения, плоские до деформации, остаются плоскими после деформации.

Классификация сил.

активные

реакции связей (пассивные)

Внешние

O

–

+

h

h

X

m = ±F·h Mo(m) = m

X

А

О

X

Л.Д.С.

Л.Д.С. – линия действия силы

Rg

Rg=

~

Л.Д.С.

А

Rg

 

 

Внутренние

С

11

12

С

N1

N2

1. Нить 2. Стержень

Р

Р

Т

 

N1

N2

3. Гладкая поверхность

 

4. Шероховатая поверхность 5. Опоры

А

В

m

RАу

RАх

RВ

шарнирно–подвижная опора

шарнирно–неподвижная опора

Gg

Ng

Fтр

 

 

6. Жёсткая заделка

RАх

RАу

МА

 

Внешние силы – силы взаимодействия между точками отдельных тел.
Внутренние силы – силы взаимодействия между точками одного и того же тела.

X

Y

Z

В курсе сопротивления материалов в основном рассматриваются внутренние силы, для определения которых используется метод сечений.

Метод сечений.

О

А

О

А

О

А

~

~

 

X

Y

Z

N

MO

О

Qx

QY

4 fcti32JW+hywLgXuGMuTGPFBDaJ0oB9wQczjq2hihuPbJQ2DeB66XYALhov5PIFwMC0LV+bO8ug6 lik23X37wJztOzNgS1/DMJ9s+qJBO2y8aWC+CiDr1L0x011W+wrgUKf+7xdQ3Br754R6XpOz3wAA AP//AwBQSwMEFAAGAAgAAAAhAE+zCQnjAAAACgEAAA8AAABkcnMvZG93bnJldi54bWxMj8FuwjAQ RO+V+g/WVuoNnIRSQoiDUCRUqSoHKJfenHhJIux1GhtI+/V1T+1xZ0czb/L1aDS74uA6SwLiaQQM qbaqo0bA8X07SYE5L0lJbQkFfKGDdXF/l8tM2Rvt8XrwDQsh5DIpoPW+zzh3dYtGuqntkcLvZAcj fTiHhqtB3kK40TyJomduZEehoZU9li3W58PFCHgttzu5rxKTfuvy5e206T+PH3MhHh/GzQqYx9H/ meEXP6BDEZgqeyHlmBYwixcB3QuYzJdPwIJjliYLYFVQljHwIuf/JxQ/AAAA//8DAFBLAQItABQA BgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADAJYD6RAgAAbgUAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2Mu eG1sUEsBAi0AFAAGAAgAAAAhAE+zCQnjAAAACgEAAA8AAAAAAAAAAAAAAAAA6wQAAGRycy9kb3du cmV2LnhtbFBLBQYAAAAABAAEAPMAAAD7BQAAAAA= " filled="f" stroked="f" strokeweight=".5pt">

MY

Mк

 

 

Тело нагружено произвольным пространством системы сил и находится в равновесии. Для нахождения внутренних сил рассекаем тело плоскостью на 2 части и одну из частей отбрасываем. Действие отброшенной части на оставшуюся часть заменяем действием внутренних сил. Все внутренние силы приводим к центру тяжести сечения (точка О) и складываем. При этом получаем главный вектор внутренних сил и главный момент внутренних сил (M_O). Раскладывая главный вектор внутренних сил по осям координат, получаем поперечные силы Q_Xи Q_Yи продольную силу N. Раскладываем главный момент внутренних сил M_Oпо осям. Получаем изгибающие моменты M_X, M_Yи крутящий момент M_K. Параметры Q_X, Q_Y, N, M_X, M_Y, M_Kназываются внутренними силовыми факторами.

Осевое растяжение, сжатие.

Стержень постоянного поперечного сечения.

– напряжение при осевом растяжении-сжатии.

 

 

Где N– продольная сила, А – площадь поперечного сечения.

;

;

.

– Закон Гука при осевом растяжении-сжатии, выраженный через ось деформации и растяжения.

длина стержня.

площадь поперечного сечения.

модуль упругости при осевом растяжении-сжатии.

– условие прочности при осевом растяжении-сжатии.

t bZ3ecNe3lbOaGA6A887gP8tbolYStUXSX7Xlr7N82NT+cViu382J+nd5zoXleXIXz90bHb553Eus /j6zH1Wbc6cL11+Ro58AAAD//wMAUEsDBBQABgAIAAAAIQACkVLv4gAAAAoBAAAPAAAAZHJzL2Rv d25yZXYueG1sTI9NS8NAEIbvgv9hGcFbu0lqP4zZlFLUUxFsheJtmp0modndkN0m6b93POlpGObh nefN1qNpRE+dr51VEE8jEGQLp2tbKvg6vE1WIHxAq7FxlhTcyMM6v7/LMNVusJ/U70MpOMT6FBVU IbSplL6oyKCfupYs386uMxh47UqpOxw43DQyiaKFNFhb/lBhS9uKisv+ahS8DzhsZvFrv7uct7fv w/zjuItJqceHcfMCItAY/mD41Wd1yNnp5K5We9EomCTP3CUomC95MrCIlwmIE5NPswhknsn/FfIf AAAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29u dGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAA LwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAM1KjjdMAwAAjQoAAA4AAAAAAAAAAAAAAAAA LgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAAKRUu/iAAAACgEAAA8AAAAAAAAAAAAA AAAApgUAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAAC1BgAAAAA= ">

допускаемое напряжение.

– закон Гука при осевом растяжении-сжатии.

 

абсолютная продольная деформация.

продольная сила.

– относительная продольная деформация.

 

;

При:

;

.

 

 

Физический смысл модуля упругости:

– относительная поперечная деформация.

Модуль упругости – есть условное напряжение, при котором длина стержня увеличивается в 2 раза.

– коэффициент Пуассона.