Потенциальная энергия при гравитационном взаимодействии

Билет 1

1. . Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.

2. Момент импульса материальной точки относительно точки O определяется векторным произведением

, где — радиус-вектор, проведенный из точки O, — импульс материальной точки. Дж*с

Билет 2

1. Гармонический осциллятор:

Кинетическая энергия записывается в виде

и потенциальная энергия есть

тогда полная энергия имеет постоянное значение Найдем импульс гармонического осциллятора. Продифференцируем выражение по t и, умножив полученный результат на массу осциллятора, получим:

2. Моментом силы относительно полюса называется физическая величина, определяемая векторным произведением радиус вектора, проведенного из данного полюса к точке приложения силы на вектор силы F. ньютон-метр

Билет 3

1. ,

2. Фаза колебаний полная — аргумент периодической функции, описывающей колебательный или волновой процесс. Гц

Билет №4

№1.1

№1.2

№2

Выражается в м/(c^2)

№3

Билет №5

№1.1

Пространство, в котором действуют консервативные силы, называется потенциальным полем. Каждой точке потенциального поля соответствует некоторое значение силы F, действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой F и U должна быть связь, с другой стороны, dA = –dU, следовательно Fdr=-dU, отсюда:

Проекции вектора силы на оси координат:

Вектор силы можно записать через проекции: , F = –grad U, где .

Градиент – это вектор, показывающий направление наибыстрейшего изменения функции. Следовательно, вектор направлен в сторону наибыстрейшего уменьшения U.

№1.2

Потенциальная энергия упругой деформации (пружины)

Найдём работу, совершаемую при деформации упругой пружины.
Сила упругости Fупр = –kx, где k – коэффициент упругости. Сила непостоянна, поэтому элементарная работа dA = Fdx = –kxdx.
(Знак минус говорит о том, что работа совершена над пружиной). Тогда 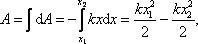, т.е. A = U1 – U2. Примем: U2 = 0, U = U1, тогда .

На рис. 5.5 показана диаграмма потенциальной энергии пружины.

Рис. 5.5
Здесь E = K + U – полная механическая энергия системы, К – кинетическая энергия в точке x1.

Потенциальная энергия при гравитационном взаимодействии

Работа тела при падении A = mgh, или A = U – U0.
Условились считать, что на поверхности Земли h = 0, U0 = 0. Тогда A = U, т.е. A = mgh.

Для случая гравитационного взаимодействия между массами M и m, находящимися на расстоянии r друг от друга, потенциальную энергию можно найти по формуле .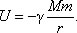

На рис. 5.4 изображена диаграмма потенциальной энергии гравитационного притяжения масс M и m.

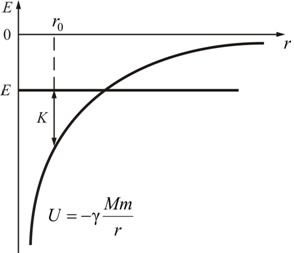
Рис. 5.4
Здесь полная энергия E = K + E. Отсюда легко найти кинетическую энергию: K = E – U.

№2

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой _n. Вектор нормального ускорения направлен по радиусу кривизны траектории. (м/с²)

№3

Билет №6

№1

№2

№3

Билет 7

1)Момент инерции Стержня -

Прямой тонкий стержень длины l и массы m

Ось перпендикулярна к стержню и проходит через его центр масс

Обруча - L = m*R^2

Диска -

Шара -

2) Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

где m — полная масса тела.

Билет 8

1) Уравнение описывает изменение движения тела конечных размеров под действием силы при отсутствии деформации и если оно движется поступательно. Для точки это уравнение справедливо всегда, поэтому его можно рассматривать как основной закон движения материальной точки.

Билет 9

1) Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.

2) - криваявфазовомпространстве, составленнаяизточек, представляющихсостояние динамическойсистемы впоследоват. моментывременивтечениевсеговремениэволюции.

Билет 10

1. Моментимпульса - векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения импульса, на вектор этого импульса

2. Угловая скорость вращения твёрдого тела относительно неподвижной оси - предел (при Δt → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt

Измеряется в рад/с.

Билет 11

1. Центр масс механической системы (МС) – точка, масса которой равна массе всей системы, авектор ускорения центра масс (в инерциальной системе отсчета) определяется только внешними силами, действующими на систему. Поэтому при нахождении закона движения системы точек можно считать, что вектор равнодействующей внешних сил приложен к центрумасс системы.
Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом

Уравнение изменения импульса МС:

Закон сохранения импульса МС: в замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

2. Угловое ускорение вращения твердого тела относительно неподвижной оси - псевдовекторная физическая величина, равная первой производной от псевдовектора угловой скорости по времени.

Измеряется в рад/c²_.

Билет 12

1. Потенциальная энергия притяжения двух материальных точек

Потенциальная энергия упругих деформаций - растяжение или сжатие пружины приводит к запасанию ее потенциальной энергии упругой деформации. Возвращение пружины к положению равновесия приводит к высвобождениюзапасенной энергии упругой деформации.

2. Импульс механической системы - векторная физическая величина, являющаяся мерой механического движения тела.

Измеряется в

Билет 13

1. Консервативные силы. Работа силы тяжести. Работа упругой силы.
В физике консервативные силы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки.
Работа силы тяжести .
Работа упругой силы

2. Дайте определение времени релаксации затухающих колебаний. Укажите единица измерения этой величины в СИ.
Временем релаксации называют промежуток времени, за который амплитуда затухающих колебаний уменьшается в е раз (е - основание натурального логарифма). Измеряется в секундах.

3. Диск диаметром равным 60 см и массой равной 1 кг вращается вокруг оси, проходящей через центр перпендикулярно его плоскости с частотой равно 20 об/c. Какую работу надо совершить, чтобы остановить диск?

Билет 14

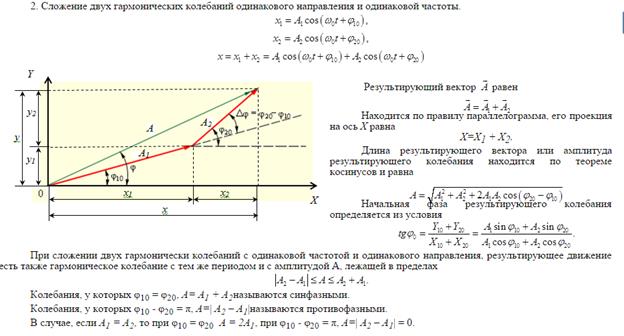
1. Гармонические колебания. Векторная диаграмма. Сложение гармонических колебаний одного направления равных частот.

Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.

Существует геометрический способ представления гармонических колебаний, заключающийся в изображении колебаний в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой (рис. 7.4).

Выберем ось . Из точки О, взятой на этой оси, отложим вектор длины , образующий с осью угол . Если привести этот вектор во вращение с угловой скоростью , то проекция конца вектора на ось будет меняться со временем по закону . Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.

Векторная диаграмма дает возможность свести сложение колебаний к геометрическому суммированию векторов.

Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты, которые имеют следующий вид:

, .

Представим оба колебания с помощью векторов и (рис. 7.5). Построим по правилу сложения векторов результирующий вектор . Легко увидеть, что проекция этого вектора на ось равна сумме проекций слагаемых векторов . Следовательно, вектор представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью , что и векторы , , так что результирующее движение будет гармоническим колебанием с частотой , амплитудой и начальной фазой . По теореме косинусов квадрат амплитуды результирующего колебания будет равен

(7.3)

Из рис. 7.5 видно, что начальная фаза результирующего колебания будет равна

2. Дайте определение момента силы относительно оси. Укажите единицы измерения этой величины в СИ.

Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.Моментом силы относительно оси называется скалярная величина, равная проекции на эту ось векторного момента силы относительно любой точки на оси.СИ: измеряется в кг*м²/c² = Н*м.

3. Из орудия массой 5 т при выстреле вылетает снаряд массой 100 кг. Кинетическая энергия снаряда при вылете 8 МДж. Какую кинетическую энергию получает орудие вследствие отдачи?

Билет 15

1. Закон сохранения механической энергии механической системы.

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

В консервативной системе все силы, действующие на тело, потенциальны и, следовательно, могут быть представлены в виде

где — потенциальная энергия материальной точки. Тогда II закон Ньютона:

где — масса частицы, — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что ,получаем

Путём элементарных операций получаем

Отсюда следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки.

2. Дайте определение кинетической энергии твердого тела при его вращении вокруг неподвижной оси. Укажите единицы измерения этой величины в СИ.

3. Шарик массой m=20 г внедряется с начальной скоростью V=20 м/с в очень массивную мишень с песком, которая движется навстречу шарику со скоростью U=10 м/с. Оценить какое количество теплоты выделится при полном торможении шарика.

Билет 16

1. Момент силы относительно оси - векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы.Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть

Момент импульса МС относительно неподвижной оси - скалярная величина, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса не зависит от положения точки 0 на оси z.

Основное уравнение динамики вращательного движения

2. Вектор ускорения - векторная величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени и показывающая на сколько изменяется вектор скорости тела при его движении за единицу времени.

Измеряется в м/с²

Билет 17

1) Момент силы - векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси, характеризует количество вращательного движения.

2) Вектор перемещения – это направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной. Модуль вектора перемещения – это длина отрезка, который соединяет начальную и конечную точки движения. (м).

Билет 18

1) Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением.Ускорение есть векторная физическая величина, определяемая как отношение малого изменения скорости

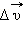к малому промежутку времени

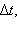за который произошло это изменение:

Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения вдоль данной данной прямой линии. Скорость равномерного движения определяется по формуле:

Радиус кривизны RR траектории в точке AA — радиус окружности, по дуге которой точка движется в данный момент времени. При этом центр этой окружности называется центром кривизны.

Физическая величина, характеризующая изменение скорости по направлению, – нормальное ускорение.