Найдём работу, совершаемую при деформации упругой пружины.
Сила упругости Fупр = –kx, где k – коэффициент упругости. Сила непостоянна, поэтому элементарная работа dA = Fdx = –kxdx.
(Знак минус говорит о том, что работа совершена над пружиной). Тогда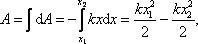 
, т.е. A = U1 – U2. Примем: U2 = 0, U = U1, тогда 
.
На рис. 5.5 показана диаграмма потенциальной энергии пружины.
Рис. 5.5
Здесь E = K + U – полная механическая энергия системы, К – кинетическая энергия в точке x1.
Потенциальная энергия при гравитационном взаимодействии
Работа тела при падении A = mgh, или A = U – U0.
Условились считать, что на поверхности Земли h = 0, U0 = 0. Тогда A = U, т.е. A = mgh.
Для случая гравитационного взаимодействия между массами M и m, находящимися на расстоянии r друг от друга, потенциальную энергию можно найти по формуле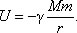 
.
На рис. 5.4 изображена диаграмма потенциальной энергии гравитационного притяжения масс M и m.
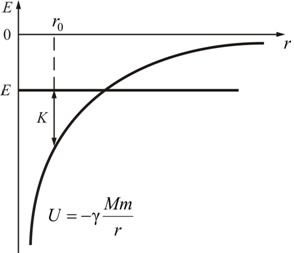
Рис. 5.4
Здесь полная энергия E = K + E. Отсюда легко найти кинетическую энергию: K = E – U.
№2
(Затухание колебаний) - постепенное ослабевание собственных колебаний, обусловленное потерями энергии колебательной системой и приводящее к уменьшению амплитуды колебаний.
№3
Билет 24
№1.1
Физи́ческийма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
№1.2
№2
Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергиисистемы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Измеряется в Ваттах.
|
|
№3
Билет 25
№1
Центром масс механической системы называется такая геометрическая точка C, сконцентрируя в которой (мысленно) массу M всей механической системы, получим, что ее статический момент массы равен статическому моменту массы всей механической системы, т.е. M⊗ rc = ∑mj⊗ rj (1.1)
Отсюда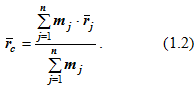 
скорость центра масс 
№2
Логарифми́ческий декреме́нт колеба́ний (декреме́нт затуха́ния; от лат. decrementum — «уменьшение, убыль») — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины x в одну и ту же сторону:
№3
Билет 26
№1
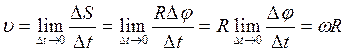
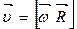
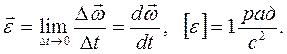
№2
В физике колебаний на оси абсцисс фазовой плоскости откладывается значения параметра x, а на оси ординат – первая производная x по времени (что, очевидно, связывает ось ординат с импульсом. См. Фазовое пространство).[2]Каждая точка фазовой плоскости отражает одно состояние системы и называется фазовой, изображающей или представляющей точкой.[3] Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется фазовой траекторией.
№3
Билет 27
№1
Свободными или собственными называются такие колебания, которые происходят в системе, предоставленной самой себе, после того как она была выведена из положения равновесия.
Примером могут служить колебания шарика, подвешенного на нити. Для того чтобы вызвать колебания, нужно либо толкнуть шарик, либо, отведя в сторону, отпустить его. При толчке шарику сообщается кинетическая энергия, а при отклонении - потенциальная.
|
|
Свободные колебания совершаются за счет первоначального запаса энергии.
Свободные колебания могут быть незатухающими только при отсутствии силы трения. В противном случае первоначальный запас энергии будет расходоваться на ее преодоление, и размах колебаний будет уменьшаться.
В физике колебаний на оси абсцисс фазовой плоскости откладывается значения параметра x, а на оси ординат – первая производная x по времени (что, очевидно, связывает ось ординат с импульсом. См. Фазовое пространство).[2]
Каждая точка фазовой плоскости отражает одно состояние системы и называется фазовой, изображающей или представляющей точкой.[3] Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется фазовой траекторией
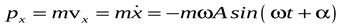
№2
Коэффициент трения скольжения — отношение силы трения к нормальной составляющей внешних сил, действующих на поверхности тела. безразмерный.
№3
