ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Многие окружающие нас процессы можно выразить с помощью числовых значений. Однако этих чисел оказывается так много и они носят различный характер, что для обыденного человека не представляют никакой информации. Каким же образом статистика позволяет исследовать социально-экономические явления? Она имеет собственную методологию, то есть систему приемов, способов и методов, направленных на изучение количественных закономерностей, проявляющихся в структуре, динамике и взаимосвязях социально-экономических явлений. Применение в статистике конкретных методов предопределяется поставленными задачами и зависит от характера исходной информации.
Основываясь на статистических данных, мы можем предсказывать развитие различных ситуаций. Что помогает нам как в технике, так и в управленческой деятельности при принятии различных решений. Именно поэтому знание основных методов статистики необходимо для того, чтобы успешно решать различного рода задачи.
Количество данных, поступающих к нам из внешнего мира, постоянно растет, поэтому статистические методы, применяемые для упорядочивания этих данных, представления их в удобном для рассмотрения и анализа виде, никогда не теряют своей актуальности.
В соответствии с поставленными задачами дадим краткую характеристику методов, применяемых на различных этапах статистического исследования.
1. Группировка — объединение единиц совокупности в некоторые группы, имеющие свои характерные особенности, общие черты и сходные размеры изучаемого признака.
Результаты группировки оформляются в виде группировочных таблиц, делающих информацию обозримой.
|
|
Группировка производится в три этапа:
- выделение группировочного признака;
- определение оптимального количества групп с равными интервалами по формуле американского ученого Стерджесса (1):
n = 1+3,322 lg N (1)
где n – необходимое число групп, N – численность единиц исследуемой совокупности.
При N=20, n=5; N=30, n=6
- расчет величины интервала по следующей формуле (2):
(2)
где хmax, хmin – наибольшее и наименьшее значение признака, n — число групп.
Средние статистические показатели.
По результатам группировки производят расчет средних величин.
Средней величиной в статистике называют обобщающий показатель, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.
Средняя арифметическая взвешенная, которая применяется для расчета среднего значения признака по сгруппированным данным, рассчитывается по формуле:
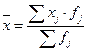(3)
где xi – центр интервала,
fi – количество единиц в j -том интервале.
Для характеристики структуры вариационного ряда определяют модальное и медианное значения, которые рассчитываются по формулам (4) и (5) соответственно:
(4)
где 
- нижняя граница модального интервала; 
- величина модального интервала; 
- частота, соответствующая модальному интервалу; 
- частота, предшествующая модальному интервалу; 
- частота интервала, следующего за модальным.
, (5)
где 
- нижняя граница медианного интервала; 
- величина медианного интервала; 
- полусумма частот ряда; 
- сумма накопленных частот, предшествующих медианному интервалу;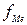 
- частота медианного интервала.
|
|