5. Относительные показатели
Относительным статистическим показателем называется обобщающая характеристика, выраженная в виде числовой меры соотношения двух сопоставляемых абсолютных величин. Такие показатели используются в различных целях: для выяснения структуры изучаемого явления, для сравнения его уровня развития с уровнем развития другого явления, для оценки происходящих в изучаемом явлении изменений и т. д.
Относительный статистический показатель получают путём деления одного абсолютного показателя на другой. Схема расчета относительного показателя выглядит следующим образом:
 где ОП – относительная величина, величина сравнения и база сравнения – сравниваемые абсолютные показатели. Таким образом, по способу получения относительные показатели всегда являются величинами производными, их можно получить только расчетным путем. Относительные показатели выражаются в разных формах - коэффициентов, процентов, промилле, продецимилле. Если база сравнения принимается за единицу, то относительный показатель выражается в форме коэффициента Если база сравнения принимается за 100 единиц, то относительный показатель выражается в процентах. По предыдущим данным рост количества родившихся составит 108,3%. Если база сравнения принимается за 1000 единиц, то относительный показатель выражается в промилле (десятая часть процента), если – за 10 000,то относительный показатель выражается в продецимилле (сотая часть процента). Промилле широко применяются в демографической статистике для характеристики рождаемости, смертности населения и других демографических процессов. Продецимилле используются для оценки обеспечения населения больничными койками, местами в высших учебных заведениях и т.д.
Следует заметить, что безразмерным по форме относительным показателям может быть приписана конкретная единица измерения. По содержанию выражаемых количественных соотношений выделяют шесть видов относительных показателей: динамики, плана и выполнения плана, структуры, координации, интенсивности и уровня
экономического развития, сравнения.
Относительный показатель динамикихарактеризует изменение изучаемого явления во времени и представляет собой соотношение показателей, характеризующих явление в текущем периоде и предшествующем (базисном) периоде. где ОП – относительная величина, величина сравнения и база сравнения – сравниваемые абсолютные показатели. Таким образом, по способу получения относительные показатели всегда являются величинами производными, их можно получить только расчетным путем. Относительные показатели выражаются в разных формах - коэффициентов, процентов, промилле, продецимилле. Если база сравнения принимается за единицу, то относительный показатель выражается в форме коэффициента Если база сравнения принимается за 100 единиц, то относительный показатель выражается в процентах. По предыдущим данным рост количества родившихся составит 108,3%. Если база сравнения принимается за 1000 единиц, то относительный показатель выражается в промилле (десятая часть процента), если – за 10 000,то относительный показатель выражается в продецимилле (сотая часть процента). Промилле широко применяются в демографической статистике для характеристики рождаемости, смертности населения и других демографических процессов. Продецимилле используются для оценки обеспечения населения больничными койками, местами в высших учебных заведениях и т.д.
Следует заметить, что безразмерным по форме относительным показателям может быть приписана конкретная единица измерения. По содержанию выражаемых количественных соотношений выделяют шесть видов относительных показателей: динамики, плана и выполнения плана, структуры, координации, интенсивности и уровня
экономического развития, сравнения.
Относительный показатель динамикихарактеризует изменение изучаемого явления во времени и представляет собой соотношение показателей, характеризующих явление в текущем периоде и предшествующем (базисном) периоде.  ОПД = текущий показатель.
Рассчитанный таким образом показатель называется коэффициентом роста (снижения). Он показывает, во сколько раз показатель текущего периода больше (меньше) показателя предшествующего (базисного) периода. Выраженный в %, относительный показатель динамики называется темпом роста (снижения)
Относительный показатель плана (прогноза) и выполнения плана
Относительный показатель плана (ОПП) и относительный показатель выполнения плана (ОПВП) используют все субъекты финансово-хозяйственной деятельности, осуществляющие текущее и стратегическое планирование. Они рассчитываются следующим образом: ОПД = текущий показатель.
Рассчитанный таким образом показатель называется коэффициентом роста (снижения). Он показывает, во сколько раз показатель текущего периода больше (меньше) показателя предшествующего (базисного) периода. Выраженный в %, относительный показатель динамики называется темпом роста (снижения)
Относительный показатель плана (прогноза) и выполнения плана
Относительный показатель плана (ОПП) и относительный показатель выполнения плана (ОПВП) используют все субъекты финансово-хозяйственной деятельности, осуществляющие текущее и стратегическое планирование. Они рассчитываются следующим образом:

 Относительный показатель выполнения плана характеризует напряженность планового задания, а относительный показатель выполнения плана – степень его выполнения.
Относительные показатели структуры (ОПС)характеризуют доли (удельные веса) составных частей совокупности в общем ее объеме. Они показывают структуру совокупности, ее строение. Расчет относительных показателей структуры заключается в исчислении удельных весов отдельных частей во всей совокупности:
Относительный показатель выполнения плана характеризует напряженность планового задания, а относительный показатель выполнения плана – степень его выполнения.
Относительные показатели структуры (ОПС)характеризуют доли (удельные веса) составных частей совокупности в общем ее объеме. Они показывают структуру совокупности, ее строение. Расчет относительных показателей структуры заключается в исчислении удельных весов отдельных частей во всей совокупности:
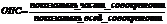 ОПС обычно выражаются в форме коэффициентов или процентах, сумма коэффициентов должна составлять 1, а сумма процентов – 100, так как удельные веса приведены к общему основанию. Относительные показатели структуры используются при изучении состава сложных явлений, распадающихся на части Совокупность относительных величин структуры показывает строение совокупности.
Относительные показатели координации (ОПК)
характеризуют отношение частей данных статистической совокупности к одной из них, взятой за базу сравнения и показывают, во сколько раз одна часть совокупности больше другой, или сколько единиц одной части совокупности приходится на 1,10,100 и т.д. единиц другой части. За базу сравнения выбирается часть, имеющая наибольший удельный вес или
являющаяся приоритетной в совокупности. Относительные показатели координации играют важную роль в экономическом анализе, так как с их помощью существующие в совокупности соотношения представляются более отчетливо и наглядно.
2.3.5. Относительные показатели интенсивности и уровня экономического развития (ОПИ) характеризуют степень распространения или уровень развития изучаемых явлений или процессов в определённой среде и образуются как результат сравнения разноименных,
но определенным образом связанных между собой величин. Указанные показатели рассчитываются следующим образом:
ОПС обычно выражаются в форме коэффициентов или процентах, сумма коэффициентов должна составлять 1, а сумма процентов – 100, так как удельные веса приведены к общему основанию. Относительные показатели структуры используются при изучении состава сложных явлений, распадающихся на части Совокупность относительных величин структуры показывает строение совокупности.
Относительные показатели координации (ОПК)
характеризуют отношение частей данных статистической совокупности к одной из них, взятой за базу сравнения и показывают, во сколько раз одна часть совокупности больше другой, или сколько единиц одной части совокупности приходится на 1,10,100 и т.д. единиц другой части. За базу сравнения выбирается часть, имеющая наибольший удельный вес или
являющаяся приоритетной в совокупности. Относительные показатели координации играют важную роль в экономическом анализе, так как с их помощью существующие в совокупности соотношения представляются более отчетливо и наглядно.
2.3.5. Относительные показатели интенсивности и уровня экономического развития (ОПИ) характеризуют степень распространения или уровень развития изучаемых явлений или процессов в определённой среде и образуются как результат сравнения разноименных,
но определенным образом связанных между собой величин. Указанные показатели рассчитываются следующим образом:
 ОПИ исчисляются в расчете на 100, 1000, 1000 и т.д. единиц изучаемой совокупности и используются в тех случаях, когда невозможно по значению абсолютного показателя определить масштаб распространения явления. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности, естественного прироста (убыли) населения как отношение числа родившихся (умерших) или величины естественного прироста за год к среднегодовой численности населения данной территории на 1000 или 10 000 человек. В эту же группу включаются относительные показатели уровня
экономического развития, характеризующие эффективность
использования ресурсов и эффективность производства. Это показатели
выработки продукции, затрат на единицу продукции, эффективности
использования производственных фондов и т.д., поскольку их получают
сопоставлением разноименных величин, относящихся к одному и тому же
явлению и одинаковому периоду времени.
2.3.6. Относительные показатели сравнения (ОПСр)
характеризуют сравнительные размеры одноименных абсолютных показателей, относящихся к различным объектам или территориям, но за одинаковый период времени. Их получают как частные от деления одноименных абсолютных показателей, характеризующих разные объекты, относящихся к одному и тому же периоду или моменту времени.
ОПИ исчисляются в расчете на 100, 1000, 1000 и т.д. единиц изучаемой совокупности и используются в тех случаях, когда невозможно по значению абсолютного показателя определить масштаб распространения явления. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности, естественного прироста (убыли) населения как отношение числа родившихся (умерших) или величины естественного прироста за год к среднегодовой численности населения данной территории на 1000 или 10 000 человек. В эту же группу включаются относительные показатели уровня
экономического развития, характеризующие эффективность
использования ресурсов и эффективность производства. Это показатели
выработки продукции, затрат на единицу продукции, эффективности
использования производственных фондов и т.д., поскольку их получают
сопоставлением разноименных величин, относящихся к одному и тому же
явлению и одинаковому периоду времени.
2.3.6. Относительные показатели сравнения (ОПСр)
характеризуют сравнительные размеры одноименных абсолютных показателей, относящихся к различным объектам или территориям, но за одинаковый период времени. Их получают как частные от деления одноименных абсолютных показателей, характеризующих разные объекты, относящихся к одному и тому же периоду или моменту времени.
 С помощью таких показателей сравнения можно сопоставлять производительность труда в разных странах и определять, где и во сколько раз она выше; сравнивать цены на различные товары, экономические показатели разных предприятий и т. д. Относительные показатели имеют важное значение в практической деятельности, но их нельзя рассматривать в отрыве от абсолютных показателей, через которые они ассчитываются, в противном случае можно прийти к неправильным выводам. Таким образом, только совместное использование абсолютных и относительных показателей позволяет провести
качественный анализ различных явлений социально-экономической жизни.
С помощью таких показателей сравнения можно сопоставлять производительность труда в разных странах и определять, где и во сколько раз она выше; сравнивать цены на различные товары, экономические показатели разных предприятий и т. д. Относительные показатели имеют важное значение в практической деятельности, но их нельзя рассматривать в отрыве от абсолютных показателей, через которые они ассчитываются, в противном случае можно прийти к неправильным выводам. Таким образом, только совместное использование абсолютных и относительных показателей позволяет провести
качественный анализ различных явлений социально-экономической жизни.
| 6. Средние показатели
Средние показатели являются наиболее распространённой формой статистических показателей, используемых в социально-экономических исследованиях. Средним называется обобщающий показатель статистической совокупности, характеризующий наиболее типичный уровень явления. Он выражает величину признака, отнесённую к единице совокупности. Особенности среднихпоказателей заключаются в том, что они, во-первых, отражают то общее, что присуще всем единицам совокупности; во-вторых, в них взаимопогашаются те отклонения значений признака, которые возникают под воздействием случайных факторов. Это означает, что средний показатель отражает типичный уровень признака, формирующийся под воздействием основных доминирующих неслучайных факторов. Применение средних величин позволяет охарактеризовать определенный признак совокупности одним числом, несмотря на то, что у разных единиц совокупности значения признака отличны друг от друга. В социально-экономическом анализе используются два класса средних величин:
- степенные средние;
- структурные средние.
К степенным средним относятся несколько видов средних, построенных по одному общему принципу:
 где xi - варианта, n=N - объем статистической совокупности, k - показатель степени.Показатель степени k может принимать любые значения, но на практике обычно используются несколько его значений: при k = 1 получают среднюю арифметическую; k = -1 – среднюю гармоническую; k = 0 – среднюю геометрическую; k =2 – среднюю квадратическую.
Степенные средние в зависимости от формы представления исходных данных могут быть простыми и взвешенными.
Если исходные данные представлены простым перечислением значений признака у статистических единиц, то используется формуластепенной средней простой: где xi - варианта, n=N - объем статистической совокупности, k - показатель степени.Показатель степени k может принимать любые значения, но на практике обычно используются несколько его значений: при k = 1 получают среднюю арифметическую; k = -1 – среднюю гармоническую; k = 0 – среднюю геометрическую; k =2 – среднюю квадратическую.
Степенные средние в зависимости от формы представления исходных данных могут быть простыми и взвешенными.
Если исходные данные представлены простым перечислением значений признака у статистических единиц, то используется формуластепенной средней простой:
 Если данные предварительно сгруппированы (представлены рядом распределения), то используется формула степенной средней взвешенной: Если данные предварительно сгруппированы (представлены рядом распределения), то используется формула степенной средней взвешенной:
 Средняя арифметическаяявляется наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности. При этом если индивидуальные значения признака у статистических единиц
заменить средней арифметической, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая есть среднее слагаемое.
Средняя арифметическая простая используется при работе с несгруппированными данными и рассчитывается по формуле: Средняя арифметическаяявляется наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности. При этом если индивидуальные значения признака у статистических единиц
заменить средней арифметической, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая есть среднее слагаемое.
Средняя арифметическая простая используется при работе с несгруппированными данными и рассчитывается по формуле:
 Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным иливариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднююсгруппированных величин. Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным иливариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднююсгруппированных величин.
 Где Где  - частость, т. е. удельный вес статистических единиц, обладающих определенным значением признака в общем объеме совокупности.
Средняя арифметическая обладает рядом полезных свойств, к важнейшим из которых относятся:
1. Средняя арифметическая постоянной величины равна этой величине: - частость, т. е. удельный вес статистических единиц, обладающих определенным значением признака в общем объеме совокупности.
Средняя арифметическая обладает рядом полезных свойств, к важнейшим из которых относятся:
1. Средняя арифметическая постоянной величины равна этой величине:
 = А при А=const;
2. Алгебраическая сумма отклонений вариант от их средней арифметической равно нулю: = А при А=const;
2. Алгебраическая сумма отклонений вариант от их средней арифметической равно нулю:
 3. Если все варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая из них уменьшится (увеличится) на это же число:
3. Если все варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая из них уменьшится (увеличится) на это же число:
 4. Если все варианты одинаково увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:
4. Если все варианты одинаково увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:
 5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится.
5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится.
 Средняя гармоническаяимеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когдастатистическая информация не содержит частот по отдельнымзначениям признака, а представлена произведением значения признака начастоту. Средняя гармоническая как вид степенной средней выглядит
следующим образом:
Средняя гармоническаяимеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когдастатистическая информация не содержит частот по отдельнымзначениям признака, а представлена произведением значения признака начастоту. Средняя гармоническая как вид степенной средней выглядит
следующим образом:
 В зависимости от формы представления исходных данных средняя гармоническая может быть рассчитана как простая и как взвешенная. Если исходные данные несгруппированны, то применяется средняягармоническая простая:
В зависимости от формы представления исходных данных средняя гармоническая может быть рассчитана как простая и как взвешенная. Если исходные данные несгруппированны, то применяется средняягармоническая простая:
 К ней прибегают в случаях определения, например, средних затрат труда, материалов и т. д. на единицу продукции по нескольким предприятиям.
При работе со сгруппированными данными используется средняя гармоническая взвешенная: К ней прибегают в случаях определения, например, средних затрат труда, материалов и т. д. на единицу продукции по нескольким предприятиям.
При работе со сгруппированными данными используется средняя гармоническая взвешенная:  где – wi статистический вес; wi = xi*ni.
Средняя геометрическая применяется в тех случаях, когда общий объем усредняемого признака является мультипликативной величиной,т.е. определяется не суммированием, а умножением индивидуальныхзначений признака. где – wi статистический вес; wi = xi*ni.
Средняя геометрическая применяется в тех случаях, когда общий объем усредняемого признака является мультипликативной величиной,т.е. определяется не суммированием, а умножением индивидуальныхзначений признака.
 Форма средней геометрической взвешенной в практических расчётах не применяется.
В социально-экономических исследованиях средняя геометрическая применяется в анализе рядов динамики при определении среднего коэффициента роста, когда задана последовательность относительных величин динамики.
Средняя геометрическая используется также для определения равноудаленной величины от максимального и минимального значения признака.
Средняя квадратическая используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин. Главная сфера её использования – измерение степени колеблемостииндивидуальных значений признака относительно средней арифметической (среднее квадратическое отклонение). Кроме этого, средняя квадратическаяприменяется в тех случаях, когда необходимо вычислить средний величину признака, выраженного в квадратных или кубических единицах измерения(при вычислении средней величины квадратных участков, средних диаметровтруб, стволов и т. д.). Средняя квадратическая рассчитывается в двух формах:
как простая Форма средней геометрической взвешенной в практических расчётах не применяется.
В социально-экономических исследованиях средняя геометрическая применяется в анализе рядов динамики при определении среднего коэффициента роста, когда задана последовательность относительных величин динамики.
Средняя геометрическая используется также для определения равноудаленной величины от максимального и минимального значения признака.
Средняя квадратическая используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин. Главная сфера её использования – измерение степени колеблемостииндивидуальных значений признака относительно средней арифметической (среднее квадратическое отклонение). Кроме этого, средняя квадратическаяприменяется в тех случаях, когда необходимо вычислить средний величину признака, выраженного в квадратных или кубических единицах измерения(при вычислении средней величины квадратных участков, средних диаметровтруб, стволов и т. д.). Средняя квадратическая рассчитывается в двух формах:
как простая  как взвешенная
как взвешенная  Все степенные средние различаются между собой значениями показателя степени.При этом, чем выше показатель степени, тем большеколичественное значение среднего показателя:
гарм х ≤ геом х ≤ арифм х ≤ кв х.
Это свойство степенных средних называется свойством мажорантности средних.
Таким образом, выбор вида среднего показателя оказывает существенное влияние на его численную величину. Выбор вида средней определяется в каждом отдельном случае путем анализа исследуемой совокупности,изучения содержания явления. Степенная средняя выбрана правильно,если на всех этапах вычислений не меняется её логическая формула, т.е.реально сохраняется социально-экономическое содержание усредняемогопризнака.
Особый вид средних показателей – структурные средние.Они используются при изучении внутреннего строения рядов распределения значений признака
Все степенные средние различаются между собой значениями показателя степени.При этом, чем выше показатель степени, тем большеколичественное значение среднего показателя:
гарм х ≤ геом х ≤ арифм х ≤ кв х.
Это свойство степенных средних называется свойством мажорантности средних.
Таким образом, выбор вида среднего показателя оказывает существенное влияние на его численную величину. Выбор вида средней определяется в каждом отдельном случае путем анализа исследуемой совокупности,изучения содержания явления. Степенная средняя выбрана правильно,если на всех этапах вычислений не меняется её логическая формула, т.е.реально сохраняется социально-экономическое содержание усредняемогопризнака.
Особый вид средних показателей – структурные средние.Они используются при изучении внутреннего строения рядов распределения значений признака
|
 , где pi – цена (стоимостная оценка единицы признака) Qi - объём признака в натуральном выражении
m – количество признаков.
Показатели, выраженные в стоимостных единицах, можно суммировать, получать по ним итоговые данные, но при их использовании необходимо учитывать изменение цен с течением времени. Для устраненияуказанного недостатка стоимостных измерителей следует применять«неизменные» или «сопоставимые» цены одного итого же периода.
Трудовые единицы измерения применяются для оценки общих затрат труда и трудоемкости отдельных операции техпроцесса. К ним относятся человеко-часы, человеко-дни (оценка затрат рабочего времени), нормо-минуты (оценка трудоёмкости). Сами по себе абсолютные показатели не дают полного представления об изучаемом явлении, не показывают его структуру, развитие во времени, соотношение между частями явления, на их основе сложно проводить
сравнения с другими подобными явлениями. Перечисленные аналитические функции выполняют относительные показатели.
, где pi – цена (стоимостная оценка единицы признака) Qi - объём признака в натуральном выражении
m – количество признаков.
Показатели, выраженные в стоимостных единицах, можно суммировать, получать по ним итоговые данные, но при их использовании необходимо учитывать изменение цен с течением времени. Для устраненияуказанного недостатка стоимостных измерителей следует применять«неизменные» или «сопоставимые» цены одного итого же периода.
Трудовые единицы измерения применяются для оценки общих затрат труда и трудоемкости отдельных операции техпроцесса. К ним относятся человеко-часы, человеко-дни (оценка затрат рабочего времени), нормо-минуты (оценка трудоёмкости). Сами по себе абсолютные показатели не дают полного представления об изучаемом явлении, не показывают его структуру, развитие во времени, соотношение между частями явления, на их основе сложно проводить
сравнения с другими подобными явлениями. Перечисленные аналитические функции выполняют относительные показатели.
 где ОП – относительная величина, величина сравнения и база сравнения – сравниваемые абсолютные показатели. Таким образом, по способу получения относительные показатели всегда являются величинами производными, их можно получить только расчетным путем. Относительные показатели выражаются в разных формах - коэффициентов, процентов, промилле, продецимилле. Если база сравнения принимается за единицу, то относительный показатель выражается в форме коэффициента Если база сравнения принимается за 100 единиц, то относительный показатель выражается в процентах. По предыдущим данным рост количества родившихся составит 108,3%. Если база сравнения принимается за 1000 единиц, то относительный показатель выражается в промилле (десятая часть процента), если – за 10 000,то относительный показатель выражается в продецимилле (сотая часть процента). Промилле широко применяются в демографической статистике для характеристики рождаемости, смертности населения и других демографических процессов. Продецимилле используются для оценки обеспечения населения больничными койками, местами в высших учебных заведениях и т.д.
Следует заметить, что безразмерным по форме относительным показателям может быть приписана конкретная единица измерения. По содержанию выражаемых количественных соотношений выделяют шесть видов относительных показателей: динамики, плана и выполнения плана, структуры, координации, интенсивности и уровня
экономического развития, сравнения.
Относительный показатель динамикихарактеризует изменение изучаемого явления во времени и представляет собой соотношение показателей, характеризующих явление в текущем периоде и предшествующем (базисном) периоде.
где ОП – относительная величина, величина сравнения и база сравнения – сравниваемые абсолютные показатели. Таким образом, по способу получения относительные показатели всегда являются величинами производными, их можно получить только расчетным путем. Относительные показатели выражаются в разных формах - коэффициентов, процентов, промилле, продецимилле. Если база сравнения принимается за единицу, то относительный показатель выражается в форме коэффициента Если база сравнения принимается за 100 единиц, то относительный показатель выражается в процентах. По предыдущим данным рост количества родившихся составит 108,3%. Если база сравнения принимается за 1000 единиц, то относительный показатель выражается в промилле (десятая часть процента), если – за 10 000,то относительный показатель выражается в продецимилле (сотая часть процента). Промилле широко применяются в демографической статистике для характеристики рождаемости, смертности населения и других демографических процессов. Продецимилле используются для оценки обеспечения населения больничными койками, местами в высших учебных заведениях и т.д.
Следует заметить, что безразмерным по форме относительным показателям может быть приписана конкретная единица измерения. По содержанию выражаемых количественных соотношений выделяют шесть видов относительных показателей: динамики, плана и выполнения плана, структуры, координации, интенсивности и уровня
экономического развития, сравнения.
Относительный показатель динамикихарактеризует изменение изучаемого явления во времени и представляет собой соотношение показателей, характеризующих явление в текущем периоде и предшествующем (базисном) периоде.  ОПД = текущий показатель.
Рассчитанный таким образом показатель называется коэффициентом роста (снижения). Он показывает, во сколько раз показатель текущего периода больше (меньше) показателя предшествующего (базисного) периода. Выраженный в %, относительный показатель динамики называется темпом роста (снижения)
Относительный показатель плана (прогноза) и выполнения плана
Относительный показатель плана (ОПП) и относительный показатель выполнения плана (ОПВП) используют все субъекты финансово-хозяйственной деятельности, осуществляющие текущее и стратегическое планирование. Они рассчитываются следующим образом:
ОПД = текущий показатель.
Рассчитанный таким образом показатель называется коэффициентом роста (снижения). Он показывает, во сколько раз показатель текущего периода больше (меньше) показателя предшествующего (базисного) периода. Выраженный в %, относительный показатель динамики называется темпом роста (снижения)
Относительный показатель плана (прогноза) и выполнения плана
Относительный показатель плана (ОПП) и относительный показатель выполнения плана (ОПВП) используют все субъекты финансово-хозяйственной деятельности, осуществляющие текущее и стратегическое планирование. Они рассчитываются следующим образом:

 Относительный показатель выполнения плана характеризует напряженность планового задания, а относительный показатель выполнения плана – степень его выполнения.
Относительные показатели структуры (ОПС)характеризуют доли (удельные веса) составных частей совокупности в общем ее объеме. Они показывают структуру совокупности, ее строение. Расчет относительных показателей структуры заключается в исчислении удельных весов отдельных частей во всей совокупности:
Относительный показатель выполнения плана характеризует напряженность планового задания, а относительный показатель выполнения плана – степень его выполнения.
Относительные показатели структуры (ОПС)характеризуют доли (удельные веса) составных частей совокупности в общем ее объеме. Они показывают структуру совокупности, ее строение. Расчет относительных показателей структуры заключается в исчислении удельных весов отдельных частей во всей совокупности:
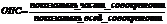 ОПС обычно выражаются в форме коэффициентов или процентах, сумма коэффициентов должна составлять 1, а сумма процентов – 100, так как удельные веса приведены к общему основанию. Относительные показатели структуры используются при изучении состава сложных явлений, распадающихся на части Совокупность относительных величин структуры показывает строение совокупности.
Относительные показатели координации (ОПК)
характеризуют отношение частей данных статистической совокупности к одной из них, взятой за базу сравнения и показывают, во сколько раз одна часть совокупности больше другой, или сколько единиц одной части совокупности приходится на 1,10,100 и т.д. единиц другой части. За базу сравнения выбирается часть, имеющая наибольший удельный вес или
являющаяся приоритетной в совокупности. Относительные показатели координации играют важную роль в экономическом анализе, так как с их помощью существующие в совокупности соотношения представляются более отчетливо и наглядно.
2.3.5. Относительные показатели интенсивности и уровня экономического развития (ОПИ) характеризуют степень распространения или уровень развития изучаемых явлений или процессов в определённой среде и образуются как результат сравнения разноименных,
но определенным образом связанных между собой величин. Указанные показатели рассчитываются следующим образом:
ОПС обычно выражаются в форме коэффициентов или процентах, сумма коэффициентов должна составлять 1, а сумма процентов – 100, так как удельные веса приведены к общему основанию. Относительные показатели структуры используются при изучении состава сложных явлений, распадающихся на части Совокупность относительных величин структуры показывает строение совокупности.
Относительные показатели координации (ОПК)
характеризуют отношение частей данных статистической совокупности к одной из них, взятой за базу сравнения и показывают, во сколько раз одна часть совокупности больше другой, или сколько единиц одной части совокупности приходится на 1,10,100 и т.д. единиц другой части. За базу сравнения выбирается часть, имеющая наибольший удельный вес или
являющаяся приоритетной в совокупности. Относительные показатели координации играют важную роль в экономическом анализе, так как с их помощью существующие в совокупности соотношения представляются более отчетливо и наглядно.
2.3.5. Относительные показатели интенсивности и уровня экономического развития (ОПИ) характеризуют степень распространения или уровень развития изучаемых явлений или процессов в определённой среде и образуются как результат сравнения разноименных,
но определенным образом связанных между собой величин. Указанные показатели рассчитываются следующим образом:
 ОПИ исчисляются в расчете на 100, 1000, 1000 и т.д. единиц изучаемой совокупности и используются в тех случаях, когда невозможно по значению абсолютного показателя определить масштаб распространения явления. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности, естественного прироста (убыли) населения как отношение числа родившихся (умерших) или величины естественного прироста за год к среднегодовой численности населения данной территории на 1000 или 10 000 человек. В эту же группу включаются относительные показатели уровня
экономического развития, характеризующие эффективность
использования ресурсов и эффективность производства. Это показатели
выработки продукции, затрат на единицу продукции, эффективности
использования производственных фондов и т.д., поскольку их получают
сопоставлением разноименных величин, относящихся к одному и тому же
явлению и одинаковому периоду времени.
2.3.6. Относительные показатели сравнения (ОПСр)
характеризуют сравнительные размеры одноименных абсолютных показателей, относящихся к различным объектам или территориям, но за одинаковый период времени. Их получают как частные от деления одноименных абсолютных показателей, характеризующих разные объекты, относящихся к одному и тому же периоду или моменту времени.
ОПИ исчисляются в расчете на 100, 1000, 1000 и т.д. единиц изучаемой совокупности и используются в тех случаях, когда невозможно по значению абсолютного показателя определить масштаб распространения явления. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности, естественного прироста (убыли) населения как отношение числа родившихся (умерших) или величины естественного прироста за год к среднегодовой численности населения данной территории на 1000 или 10 000 человек. В эту же группу включаются относительные показатели уровня
экономического развития, характеризующие эффективность
использования ресурсов и эффективность производства. Это показатели
выработки продукции, затрат на единицу продукции, эффективности
использования производственных фондов и т.д., поскольку их получают
сопоставлением разноименных величин, относящихся к одному и тому же
явлению и одинаковому периоду времени.
2.3.6. Относительные показатели сравнения (ОПСр)
характеризуют сравнительные размеры одноименных абсолютных показателей, относящихся к различным объектам или территориям, но за одинаковый период времени. Их получают как частные от деления одноименных абсолютных показателей, характеризующих разные объекты, относящихся к одному и тому же периоду или моменту времени.
 С помощью таких показателей сравнения можно сопоставлять производительность труда в разных странах и определять, где и во сколько раз она выше; сравнивать цены на различные товары, экономические показатели разных предприятий и т. д. Относительные показатели имеют важное значение в практической деятельности, но их нельзя рассматривать в отрыве от абсолютных показателей, через которые они ассчитываются, в противном случае можно прийти к неправильным выводам. Таким образом, только совместное использование абсолютных и относительных показателей позволяет провести
качественный анализ различных явлений социально-экономической жизни.
С помощью таких показателей сравнения можно сопоставлять производительность труда в разных странах и определять, где и во сколько раз она выше; сравнивать цены на различные товары, экономические показатели разных предприятий и т. д. Относительные показатели имеют важное значение в практической деятельности, но их нельзя рассматривать в отрыве от абсолютных показателей, через которые они ассчитываются, в противном случае можно прийти к неправильным выводам. Таким образом, только совместное использование абсолютных и относительных показателей позволяет провести
качественный анализ различных явлений социально-экономической жизни.
 где xi - варианта, n=N - объем статистической совокупности, k - показатель степени.Показатель степени k может принимать любые значения, но на практике обычно используются несколько его значений: при k = 1 получают среднюю арифметическую; k = -1 – среднюю гармоническую; k = 0 – среднюю геометрическую; k =2 – среднюю квадратическую.
Степенные средние в зависимости от формы представления исходных данных могут быть простыми и взвешенными.
Если исходные данные представлены простым перечислением значений признака у статистических единиц, то используется формуластепенной средней простой:
где xi - варианта, n=N - объем статистической совокупности, k - показатель степени.Показатель степени k может принимать любые значения, но на практике обычно используются несколько его значений: при k = 1 получают среднюю арифметическую; k = -1 – среднюю гармоническую; k = 0 – среднюю геометрическую; k =2 – среднюю квадратическую.
Степенные средние в зависимости от формы представления исходных данных могут быть простыми и взвешенными.
Если исходные данные представлены простым перечислением значений признака у статистических единиц, то используется формуластепенной средней простой:
 Если данные предварительно сгруппированы (представлены рядом распределения), то используется формула степенной средней взвешенной:
Если данные предварительно сгруппированы (представлены рядом распределения), то используется формула степенной средней взвешенной:
 Средняя арифметическаяявляется наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности. При этом если индивидуальные значения признака у статистических единиц
заменить средней арифметической, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая есть среднее слагаемое.
Средняя арифметическая простая используется при работе с несгруппированными данными и рассчитывается по формуле:
Средняя арифметическаяявляется наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности. При этом если индивидуальные значения признака у статистических единиц
заменить средней арифметической, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая есть среднее слагаемое.
Средняя арифметическая простая используется при работе с несгруппированными данными и рассчитывается по формуле:
 Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным иливариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднююсгруппированных величин.
Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным иливариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднююсгруппированных величин.
 Где
Где  - частость, т. е. удельный вес статистических единиц, обладающих определенным значением признака в общем объеме совокупности.
Средняя арифметическая обладает рядом полезных свойств, к важнейшим из которых относятся:
1. Средняя арифметическая постоянной величины равна этой величине:
- частость, т. е. удельный вес статистических единиц, обладающих определенным значением признака в общем объеме совокупности.
Средняя арифметическая обладает рядом полезных свойств, к важнейшим из которых относятся:
1. Средняя арифметическая постоянной величины равна этой величине:
 = А при А=const;
2. Алгебраическая сумма отклонений вариант от их средней арифметической равно нулю:
= А при А=const;
2. Алгебраическая сумма отклонений вариант от их средней арифметической равно нулю:
 3. Если все варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая из них уменьшится (увеличится) на это же число:
3. Если все варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая из них уменьшится (увеличится) на это же число:
 4. Если все варианты одинаково увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:
4. Если все варианты одинаково увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:
 5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится.
5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится.
 Средняя гармоническаяимеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когдастатистическая информация не содержит частот по отдельнымзначениям признака, а представлена произведением значения признака начастоту. Средняя гармоническая как вид степенной средней выглядит
следующим образом:
Средняя гармоническаяимеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когдастатистическая информация не содержит частот по отдельнымзначениям признака, а представлена произведением значения признака начастоту. Средняя гармоническая как вид степенной средней выглядит
следующим образом:
 В зависимости от формы представления исходных данных средняя гармоническая может быть рассчитана как простая и как взвешенная. Если исходные данные несгруппированны, то применяется средняягармоническая простая:
В зависимости от формы представления исходных данных средняя гармоническая может быть рассчитана как простая и как взвешенная. Если исходные данные несгруппированны, то применяется средняягармоническая простая:
 К ней прибегают в случаях определения, например, средних затрат труда, материалов и т. д. на единицу продукции по нескольким предприятиям.
При работе со сгруппированными данными используется средняя гармоническая взвешенная:
К ней прибегают в случаях определения, например, средних затрат труда, материалов и т. д. на единицу продукции по нескольким предприятиям.
При работе со сгруппированными данными используется средняя гармоническая взвешенная:  где – wi статистический вес; wi = xi*ni.
Средняя геометрическая применяется в тех случаях, когда общий объем усредняемого признака является мультипликативной величиной,т.е. определяется не суммированием, а умножением индивидуальныхзначений признака.
где – wi статистический вес; wi = xi*ni.
Средняя геометрическая применяется в тех случаях, когда общий объем усредняемого признака является мультипликативной величиной,т.е. определяется не суммированием, а умножением индивидуальныхзначений признака.
 Форма средней геометрической взвешенной в практических расчётах не применяется.
В социально-экономических исследованиях средняя геометрическая применяется в анализе рядов динамики при определении среднего коэффициента роста, когда задана последовательность относительных величин динамики.
Средняя геометрическая используется также для определения равноудаленной величины от максимального и минимального значения признака.
Средняя квадратическая используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин. Главная сфера её использования – измерение степени колеблемостииндивидуальных значений признака относительно средней арифметической (среднее квадратическое отклонение). Кроме этого, средняя квадратическаяприменяется в тех случаях, когда необходимо вычислить средний величину признака, выраженного в квадратных или кубических единицах измерения(при вычислении средней величины квадратных участков, средних диаметровтруб, стволов и т. д.). Средняя квадратическая рассчитывается в двух формах:
как простая
Форма средней геометрической взвешенной в практических расчётах не применяется.
В социально-экономических исследованиях средняя геометрическая применяется в анализе рядов динамики при определении среднего коэффициента роста, когда задана последовательность относительных величин динамики.
Средняя геометрическая используется также для определения равноудаленной величины от максимального и минимального значения признака.
Средняя квадратическая используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин. Главная сфера её использования – измерение степени колеблемостииндивидуальных значений признака относительно средней арифметической (среднее квадратическое отклонение). Кроме этого, средняя квадратическаяприменяется в тех случаях, когда необходимо вычислить средний величину признака, выраженного в квадратных или кубических единицах измерения(при вычислении средней величины квадратных участков, средних диаметровтруб, стволов и т. д.). Средняя квадратическая рассчитывается в двух формах:
как простая  как взвешенная
как взвешенная  Все степенные средние различаются между собой значениями показателя степени.При этом, чем выше показатель степени, тем большеколичественное значение среднего показателя:
гарм х ≤ геом х ≤ арифм х ≤ кв х.
Это свойство степенных средних называется свойством мажорантности средних.
Таким образом, выбор вида среднего показателя оказывает существенное влияние на его численную величину. Выбор вида средней определяется в каждом отдельном случае путем анализа исследуемой совокупности,изучения содержания явления. Степенная средняя выбрана правильно,если на всех этапах вычислений не меняется её логическая формула, т.е.реально сохраняется социально-экономическое содержание усредняемогопризнака.
Особый вид средних показателей – структурные средние.Они используются при изучении внутреннего строения рядов распределения значений признака
Все степенные средние различаются между собой значениями показателя степени.При этом, чем выше показатель степени, тем большеколичественное значение среднего показателя:
гарм х ≤ геом х ≤ арифм х ≤ кв х.
Это свойство степенных средних называется свойством мажорантности средних.
Таким образом, выбор вида среднего показателя оказывает существенное влияние на его численную величину. Выбор вида средней определяется в каждом отдельном случае путем анализа исследуемой совокупности,изучения содержания явления. Степенная средняя выбрана правильно,если на всех этапах вычислений не меняется её логическая формула, т.е.реально сохраняется социально-экономическое содержание усредняемогопризнака.
Особый вид средних показателей – структурные средние.Они используются при изучении внутреннего строения рядов распределения значений признака