Задание 1.
Решение:
Построим поле корреляции.
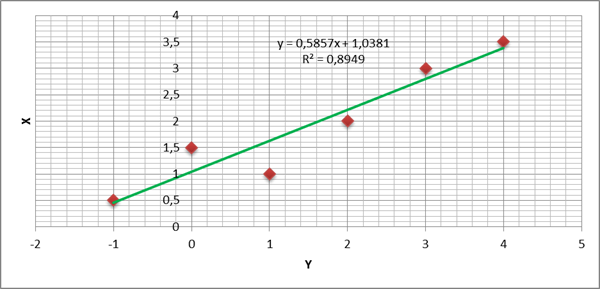
Рисунок 1. Поле корреляции.
Анализируя расположение точек поля корреляции, предполагаем, что связь между признаками х и у может быть линейной, т.е. 
.
Рассчитаем параметры линейной регрессии методом наименьших квадратов.
| № | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| -1 | 0,5 | -0,5 | 0,25 | 0,452 | 0,048 | 0,002 | 0,095 | 2,0079 | ||
| 1,5 | 2,25 | 1,038 | 0,462 | 0,213 | 0,308 | 0,1739 | ||||
| 1,624 | -0,624 | 0,389 | 0,624 | 0,8409 | ||||||
| 2,210 | -0,210 | 0,044 | 0,105 | 0,0069 | ||||||
| 2,795 | 0,205 | 0,042 | 0,068 | 1,1729 | ||||||
| 3,5 | 12,25 | 3,381 | 0,119 | 0,014 | 0,034 | 2,5059 | ||||
| Сумма | 11,5 | 27,5 | 28,75 | 0,705 | 1,234 | 6,7083 | ||||
| Среднее | 1,5 | 1,917 | 4,583 | 5,167 | 4,792 | - | - | - | - | - |
Уравнение линии регрессии для линейной зависимости имеет вид 
, коэффициенты a и b находятся из системы уравнений:
Подставив полученные значения в систему, получаем:
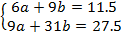
Решив систему, получим 
. Следовательно, уравнение линии регрессии:
С увеличением X на 1 ед., Y в среднем увеличиться на 1,0381 ед.
Тесноту связи оценим с помощью линейного коэффициента парной корреляции. Предварительно определим средние квадратические отклонения признаков.
Откуда коэффициент корреляции:
Между признаками X и Y наблюдается очень высокая, прямая линейная корреляционная связь.
Определим среднюю относительную ошибку Аппроксимации:
Ошибка небольшая. Качество модели высокое.
Коэффициент детерминации:
Это означает, что Y на 89.49% зависит от X. Остальные 10,51% припадают на стохастическую компоненту та на факторы, которые не включены в модель.
Примем α = 0,05. Найдем табличное (критическое) значение F- критерия Фишера:
Найдем фактическое значение F - критерия Фишера:
Так как 
Рассчитаем прогнозное значение. Точечный прогноз:
Вывод: анализируя расположение точек поля корреляции, было предположено, что связь между признаками х и у может быть линейной, т.е. .
Методом наименьших квадратов было найдено следующее уравнение, описывающее зависимость:
С увеличением X на 1 ед., Y в среднем увеличиться на 1,0381 ед.
Между признаками X и Y была установлена очень высокая, прямая линейная корреляционная связь. Y на 89.49% зависит от X. Остальные 10,51% припадают на стохастическую компоненту та на факторы, которые не включены в модель.
При увеличении среднего уровня на 110% величина У будет на уровне 2,0045.
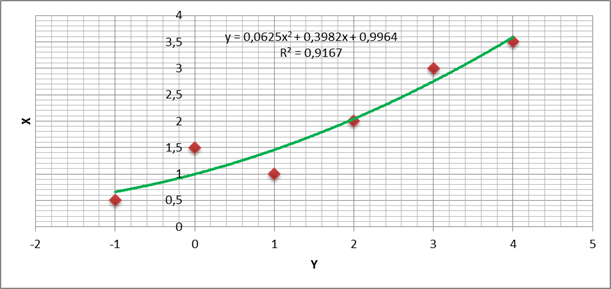
Рассчитаем параметры квадратичной регрессии методом наименьших квадратов.
| № |
|
|
|
|
| 
| 
| 
|
| -1 | 0,5 | -0,5 | 0,25 | -1 | 0,5 | |||
| 1,5 | 2,25 | |||||||
| 3,5 | 12,25 | |||||||
| Всего | 11,5 | 27,5 | 28,75 | 92,5 | ||||
| Сред. | 1,5 | 1,9174 | - | - | - | - | - | - |
| № |
|
| 
|
|
|
|
| -1 | 0,5 | 0,661 | 0.0258 | 0.321 | 2,0079 | |
| 1,5 | 0,996 | 0.254 | 0.336 | 0,1739 | ||
| 1,457 | 0.209 | 0.457 | 0,8409 | |||
| 2,043 | 0.00184 | 0.0214 | 0,0069 | |||
| 2,754 | 0.0607 | 0.0821 | 1,1729 | |||
| 3,5 | 3,589 | 0.00797 | 0.0255 | 2,5059 | ||
| Всего | 11,5 | 11,5 | 0.559 | 1.243 | 6,7083 |
Уравнение линии регрессии для линейной зависимости имеет вид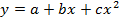 
, коэффициенты 
находятся из системы уравнений:
Подставив полученные значения в систему, получаем:
Решим систему методом Крамера.
Найдем определитель основной матрицы:
, то заданая за теоремой Крамера СЛАУ имеет единое решение.
Найдем определители 
полученные из определителя 
, заменой соответствующего 1-ого, 2-ого, 3-ого столбика столбиком свободных переменных:
,
,
.
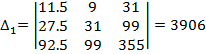За формулой Крамера:
Получим 
. Следовательно, уравнение линии регрессии:
Индекс корреляции:
Между признаками X и Y наблюдается очень высокая линейная корреляционная связь.
Определим среднюю относительную ошибку Аппроксимации:
Ошибка большая. Качество модели низкое.
Коэффициент детерминации:
Это означает, что Y на 91.67% зависит от X. Остальные 8,33% припадают на стохастическую компоненту та на факторы, которые не включены в модель.
Примем α = 0,05. Найдем табличное (критическое) значение F- критерия Фишера:
Найдем фактическое значение F - критерия Фишера:
Так как
Рассчитаем прогнозное значение. Точечный прогноз:
Вывод: Методом наименьших квадратов было найдено следующее квадратное уравнение, описывающее зависимость:
Между признаками X и Y была установлена очень высокая линейная корреляционная связь. Y на 91.67% зависит от X. Остальные 8,33% припадают на стохастическую компоненту та на факторы, которые не включены в модель.
При увеличении среднего уровня на 110% величина У будет на уровне 1,8229.
Уровень качества квадратной регрессии немного выше, чем линейной.