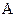Сложение колебаний.
При всех сложениях колебаний различают сложение колебаний, совершающихся в одном направлении и сложение колебаний, совершающихся во взаимно перпендикулярных направлениях.
Колебания можно представлять в векторной форме, а, именно, колебание вида 
представляют в виде вектора (рис.1), модуль которого равен амплитуде колебаний и который вращается с угловой скоростью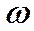 
против часовой стрелки.
Сложение одинаково направленных колебаний
Рассмотрим вначале сложение двух одинаково направленных колебаний одинаковой частоты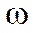 
: 
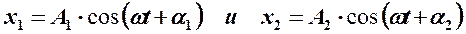. Ясно, что результирующее колебание будет иметь ту же частоту и какие-то неизвестные амплитуду 
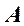и начальную фазу 
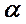, которые надо определить:
.
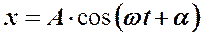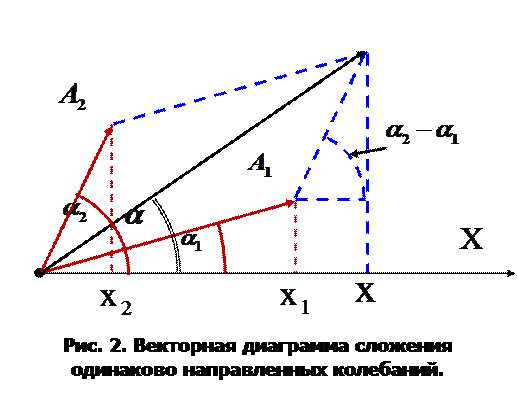
Для их нахождения построим векторную диаграмму (рис. 2).
Согласно теореме косинусов, для определения результирующей амплитуды можно записать следующее равенство.
|
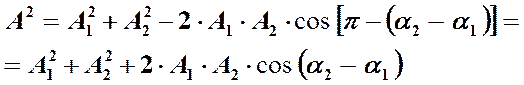
Отсюда, выражение для результирующей амплитуды будет иметь вид:
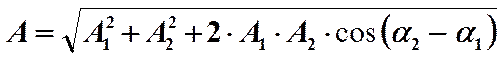
Также из рис.2 легко получить выражение для определения начальной фазы результирующего колебания:
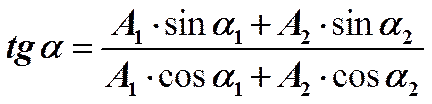
Биения
Особый интерес представляет сложение одинаково направленных колебаний с мало отличающимися частотами, т.е. биения.
Пусть, например, одно колебание имеет вид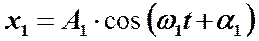 
, а второе 
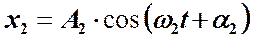. Для упрощения выкладок, можно положить 
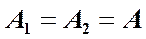и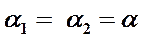 
. Кроме того, как уже говорилось, частоты мало отличаются друг от друга, т.е.: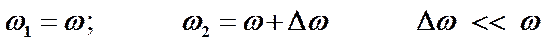 
В этом случае складываемые колебания запишем как:
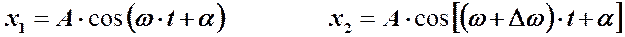
При этом, согласно известному тригонометрическому равенству (
), можно записать:
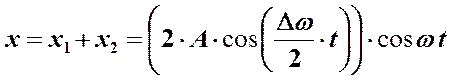
Амплитуда колебаний очевидно будет равна:
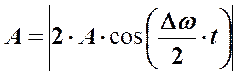
и, следовательно, она будет меняться с вдвое большей частотой, а период биений будет равен:
 |
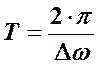
График биений будет иметь вид, изображенный на рис. 3
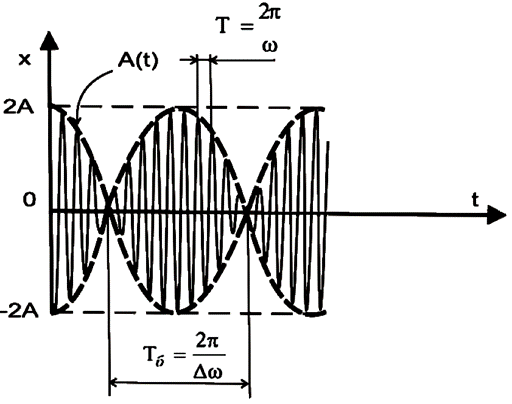
Т.е. имеются колебания основной частоты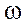 
, но амплитуда этих колебаний меняется с течением времени также по гармоническому закону, но с гораздо большим периодом.
Сложение взаимно перпендикулярных колебаний
Колебания могут происходить и во взаимно перпендикулярных направлениях. Например, математический маятник может совершать колебания по двум взаимно перпендикулярным направлениям.
Пусть колебания такого маятника в плоскости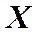 
совершаются по закону
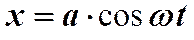
а в плоскости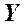 
по закону
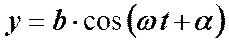
где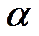 
‑ разность фаз между этими колебаниям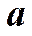и, 
и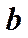 
‑ амплитуды этих колебаний.
Получим уравнение траектории результирующего колебания в явном виде, для чего исключим параметр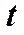 
.
Из первого уравнения вытекает:
Подставим эти значения тригонометрических функций во второе уравнение, для чего предварительно разложим выражение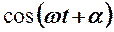 
:
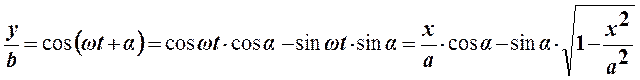
Возведем в квадрат левую и правую части:
Отсюда получим окончательно:
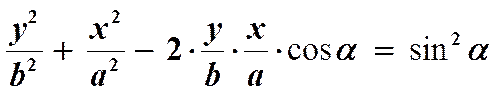
Уравнение представляет собой уравнение траектории при сложении двух взаимно перпендикулярных колебаний.
Рассмотри некоторые частные случаи.
1. 
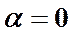Т.е. между колебаниями нет сдвига фаз.
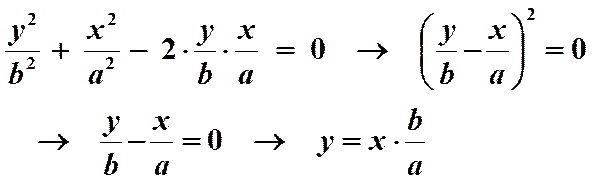
Т.е. траектория представляет собой прямую линию (см. рис. 4 I-й и III-й квадранты).
2. 
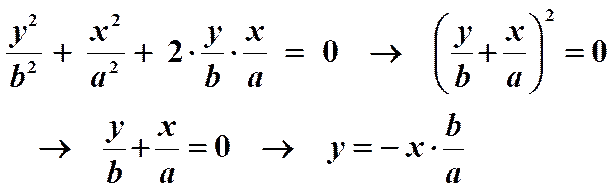Т.е. траектория также представляет собой прямую линию (см. рис.4 II-й и IV-й квадранты).
3. 
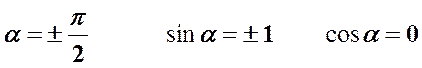. Уравнение траектории представляет собой эллипс (см. рис. 5).
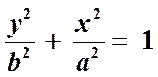
Если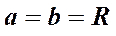 
, то вместо эллипса получится окружность радиуса 
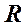. Знаки 
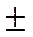отмечают направления обхода (см. рис. 5а).
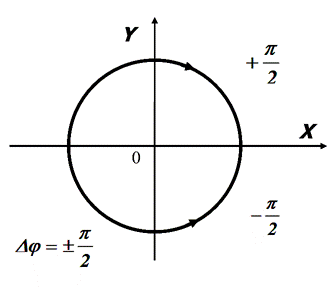
Рис. 5а
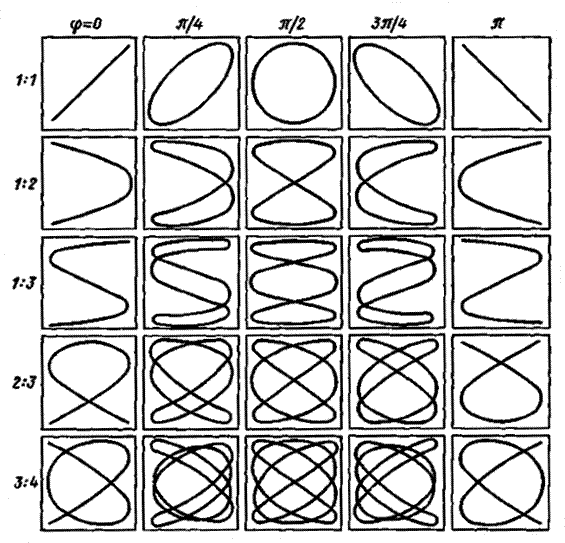
Фигуры Лиссажу
Если частоты складываемых колебаний не одинаковы, но кратны друг другу, то получаются более сложные фигуры, которые называются фигурами Лиссажу. На рис. 6 и рис.7 приведены некоторые такие фигуры.
 |
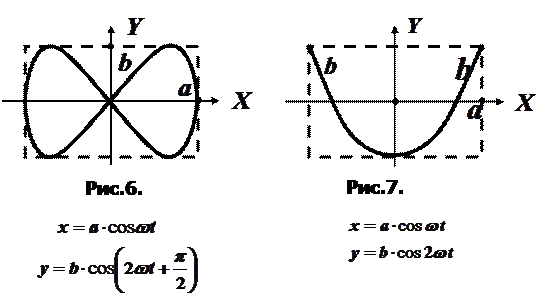Если же частоты складываемых колебаний не одинаковы и не кратны друг другу, то траектория представляет собой не замкнутую кривую, которая постепенно, с течением времени, заполнит собой весь прямоугольник со сторонами
.
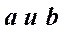Проследим зависимость фигур Лиссажу от соотношения частот при постоянной разности фаз, равной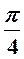 
на след. рисунке
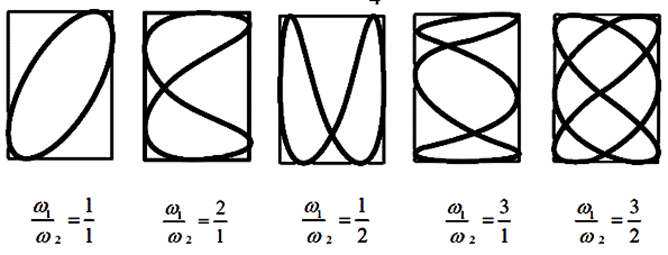
Фигуры Лиссажу при разных соотношениях частот и разностях фаз складываемых колебаний представлены ниже:
