Глава 4
Аналитическая геометрия на плоскости и в пространстве
Прямая на плоскости. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой и его исследование
Общее уравнение прямой на плоскости
Определение 29.1: Под прямой линией будем понимать геометрическое место точек l такое, что для любых двух точек M 
и M из данного множества вектор 
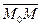коллинеарен заданному ненулевому вектору 
.
(29.5)
и 
(29.6)
ЗАДАЧА. Доказать, что если векторы 
и 
ортогональны некоторому вектору 
, то 
и 
коллинеарные.
Определение 29.2: Уравнение (29.5) с условием (29.6) называется общим уравнением прямой линии на плоскости.
Определение 29.3: А вектор 
называется нормальным вектором (или нормалью) к прямой l, заданной уравнением (29.5).
Как уже было показано, вектор 
, то есть 
Исследование общего уравнения прямой на плоскости
(29.9)
Уравнение прямой с угловым коэффициентом
(29.10)
Определение 29.4: Поэтому уравнение (29.10) называется уравнение прямой с угловым коэффициентом (а множитель k- её угловым коэффициентом).
К уравнению 29.10 можно свести всякую прямую, не коллинеарную оси ординат (если 
OY, то есть l 
OX, то 
и 
).
Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
Случай уравнения прямых с угловыми коэффициентами
 |
|
(30.4)
То есть угол между прямыми 
и 
можно найти по формуле (30.4).
|
и .
1. Условие параллельности: 
(см. черт. 30.2) 
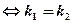(30.5)
(и 
, иначе 
)
2. Условие перпендикулярности: 
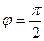(см. чертеж 30.1) 
(см. равенство(30.4)) 
(30.6)
3. Точка пересечения прямых и .
Абсциссу точки пересечения прямых можно найти приравняв, правые части уравнений (30.1) и (30.2):
Решая уравнение (30.7), получим
А подставив полученную в (30.8) абсциссу точки пересечения прямых в уравнение (30.1) (или в (30.2)), найдем и ординату их точки пересечения:
= 
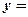
Случай общего уравнения прямых линий
| |||
 | |||
l1
Пусть прямые и заданы уравнениями:
|
|
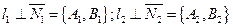
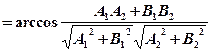(30.12)
Координаты точки пересечения прямых и можно найти, решая систему из двух линейных уравнений (30.10) и (30.11). По формулам Крамера (см. §8) имеем:
|
x=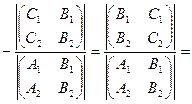 
y=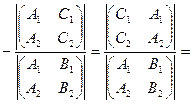 
Для взаимного расположения прямых и рассмотрим матрицы:
и 
1. 
= 
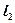
(30.14).
2. || 
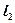
(30.15)
3. и 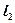пересекаются в одной точке 
(30.16)
Условие перпендикулярности прямых и :
= 
(30.14)
(
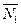– нормаль к прямой , а 
– нормаль к прямой (см. чертёж 30.3))
Уравнение прямой на плоскости по двум точкам и «в отрезках»
31.1 Уравнение прямой проходящей через точку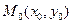 
и коллинеарной заданному вектору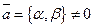 
Её уравнение имеет вид 
,
или 
(см. уравнение (29.4))
31.2 Уравнение прямой проходящей через заданную точку 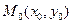и ортогональной заданному вектору 
(см. уравнение (29.8)).
31.3 Уравнение прямой проходящей через две заданные точки 
и 
Это уравнение имеет вид:
(31.1)
В случае 
в (31.1) у можно выразить через x:
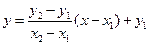(31.2)
А для и 
уравнение (31.1) можно записать следующим образом:
Уравнение прямой «в отрезках»
 | |||
| |||
(29.9)
Определение 31.1: Поэтому уравнение (29.9) называется уравнением прямой «в отрезках».
Расстояние от точки до прямой на плоскости
ЗАДАЧА. Доказать, что координаты проекции точки M*(x*,y*) на прямую l, заданную уравнением (29.5), можно найти по формулам (32.2).
(32.2)
Итак, расстояние от точки M*(x*,y*) до прямой l, задаётся уравнением (29.5), можно найти по формуле:
(32.3)
Эллипс, как кривая второго порядка. Его полуоси, эксцентриситет, фокусы и директрисы. Окружность в качестве частного случая эллипса.
Эллипс, как кривая второго порядка.
Определение 33.2. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.
отрезку (рис. 33.1).
Теорема 33.1. Пусть сумма расстояний от точки эллипса до фокусов равна 2a, а расстояние между фокусами –– 2c. Тогда в выбранной системе координат эллипс имеет уравнение
| (33.2) |
где
| (33.5) |
| (33.4) |
Определение 33.3. Уравнение (33.4) называется каноническим уравнением эллипса.