Задания к зачету
1 вариант
Задания ознакомительного уровня усвоения материала:
1) Примените свойство логарифмов 
1) 
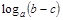
| 2) 
| 3) 
| 4)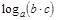 
|
Прямая называется перпендикулярной плоскости, если она
1) перпендикулярна двум пересекающимся прямым плоскости;
2) перпендикулярна некоторой прямой плоскости;
3) перпендикулярна любой прямой, лежащей в плоскости;
4) перпендикулярна двум параллельным прямым плоскости.
3) Выберите верное утверждение:
1) Через три точки проходит плоскость и при том только одна;
2) Через две пересекающиеся прямые проходит плоскость и при том только одна;
3) Через прямую и точку проходит плоскость и при том только одна;
4) Через две скрещивающиеся прямые проходит плоскость и при том только одна.
4) Закончите формулировку признака: если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые _______________
| 1) пересекающиеся | 2) скрещивающиеся | 3) параллельные | 4) нет верного варианта ответа |
5) В какой координатной четверти лежит угол 
| 1) в 1 четверти | 2) во 2 четверти | 3) в 3 четверти | 4) в 4 четверти |
6) 
равен
1) 
| 3)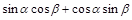 
|
2) 
| 4)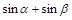 
|
7) 
равна
1) 
| 3) 
|
2) 
| 4) 
|
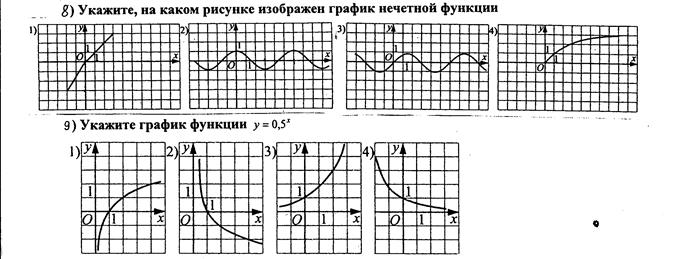
Задания репродуктивного уровня усвоения материала:
10) Постройте график функции 
, выберите промежутки, на которых она возрастает:
1) 
| 2) 
| 3) 
| 4) 
|
11) Постройте график функции 
, выберите промежуток, где 
1) 
| 2) 
| 3) 
| 4) 
|
12) Упростите выражение 
1) 
| 2) 
| 3)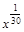 
| 4)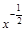 
|
13) Внесите множитель под знак корня 
1) 
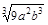
| 2) 
| 3) 
| 4) 
|
14) Вычислите 
| 1) -5 | 2) 5 | 3) 4 | 4) -16 |
15) Вычислите 
| 1) 3 | 2) 27 | 3) 9 | 4) 12 |
16) Переведите в радианную меру 85°
1) 
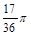
| 2)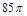 
| 3) 
| 4)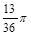 
|
17) Упростите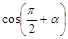 
1) 
| 2) 
| 3) 
| 4)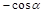 
|
18) Вычислите 
1) 
| 2) 
| 3) 
| 4) 
|
19) Найдите область определения функции 
1) 
| 2) 
| 3) 
| 4) 
|
Задания к зачету
2 вариант
Задания ознакомительного уровня усвоения материала:
1) Примените свойство логарифмов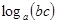 
1) 
| 2) 
| 3) 
| 4) 
|
Прямые называется скрещивающимися, если они
1) пересекаются;
2) не лежат в одной плоскости;
3) одна из двух прямых лежит в плоскости, а вторая пересекает эту плоскость в точке, не лежащей на первой прямой;
4) не имеют общих точек.
3) Выберите верное утверждение:
1) Если прямая параллельна прямой, лежащей в плоскости, то эта прямая параллельна плоскости;
2) Если прямая, не лежащая в плоскости, параллельна прямой, лежащей в плоскости, то эта прямая параллельна плоскости;
3) Если прямая, не лежащая в плоскости, параллельна двум пересекающимся прямым плоскости, то она параллельна плоскости;
4) Если прямая, не лежащая в плоскости, параллельна всем прямым плоскости, то она параллельна плоскости.
4) Закончите формулировку признака: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она _______________
1) параллельна этой плоскости 2) нет верного варианта ответа 3) скрещивается с плоскостью 4) перпендикулярна этой плоскости
5) В какой координатной четверти лежит угол 
-195°
| 1) в 1 четверти | 2) во 2 четверти | 3) в 3 четверти | 4) в 4 четверти |
6) 
равен
1) 
| 3) 
|
2) 
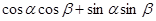
| 4)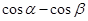 
|
7) 
равна
1) 
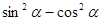
| 3) 
|
2) 
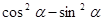
| 4)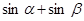 
|
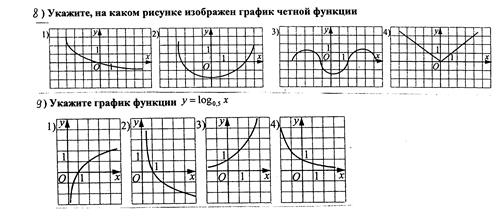
Задания репродуктивного уровня усвоения материала:
10) Постройте график функции 
, выберите промежутки, на которых она убывает
1) 
3) 
| 2) 
4) 
|
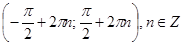
11) Постройте график функции 
, запишите нули функции:
1) 
| 2)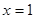 
| 3)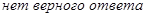 
| 4)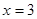 
|
12) Упростите выражение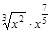 
1) 
| 2) 
| 3)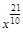 
| 4) 
|
13) Вынесите множитель из-под знака корня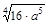 
, считая, что a>0
1) 
| 2)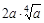 
| 3) 
| 4)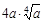 
|
14) Вычислите 
| 1) 3 | 2) -3 | 3) -9 | 4)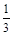 
|
15) Вычислите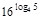 
| 1) 5 | 2) 25 | 3) 16 | 4) 10 |
16) Переведите в градусную меру 
| 1) 75° | 2) 150° | 3) 125° | 4) -75° |
17) Упростите 
1) 
| 2)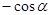 
| 3)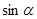 
| 4)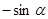 
|
18) Вычислите 
1) 
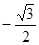
| 2) 
| 3)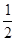 
| 4) 
|
19) Найдите область определения функции 
1) 
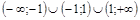
| 2) 
| 3) 
| 4)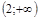 
|
Критерии оценки выполнения заданий
- Ключи к заданиям и критерии оценки:
| Ключи и модельные ответы к заданиям | Баллы |
Вариант 1
Задания ознакомительного уровня усвоения материала:
| По 1 баллу По 2 балла По 1 баллу По 2 балла |
2. Аналитическая шкала
| Количество баллов | Результат |
| 0 – 11 | |
| 12 – 19 | |
| 20 – 24 | |
| 25 – 29 |
Преподаватель Мелёхина Т.Н.