 |
Рисунок 27 – Третье элементарное измерение
Если подставить в уравнение (3.1) значения XC, YC и R, то получится сложное уравнение второй степени относительно неизвестных X и Y. Из одного уравнения два неизвестных найти невозможно, следовательно, измерения одного угла β на определяемой точке недостаточно для определения двух координат этой точки.
Для однозначного определения двух координат точки P нужно выполнить измерение двух элементов. Количество комбинаций из трёх по два равно шести; комбинации двух элементарных измерений для определения координат одной точки называются геодезическими засечками.
1. Измеряются один угол и одно расстояние; оба измерения выполняются на пункте A, – полярная засечка;
2. Измеряются два угла; один угол измеряется на пункте A, другой - на пункте B, - прямая угловая засечка;
3. Измеряются два расстояния; одно расстояние - от пункта A до пункта P, другое – от пункта B до пункта P, - линейная засечка;
4. Измеряются два угла; оба измерения выполняются на точке P; один угол − между направлениями на исходные пункты A и B, другой – между направлениями на исходные пункты B и D, - обратная угловая засечка.
Пятая и шестая комбинации названий не имеют и для определения координат точки P не применяются.
3.3.3. Полярная засечка
В полярной засечке исходными данными являются координаты пункта А и дирекционный угол  направления АВ (если дирекционный угол
направления АВ (если дирекционный угол  не задан, нужно решить обратную геодезическую задачу между пунктами А и В и вычислить его); измеряемыми данными являются горизонтальный угол
не задан, нужно решить обратную геодезическую задачу между пунктами А и В и вычислить его); измеряемыми данными являются горизонтальный угол  (средняя квадратическая ошибка измерения угла
(средняя квадратическая ошибка измерения угла 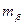 ) и расстояние
) и расстояние  (относительная ошибка измерения расстояния
(относительная ошибка измерения расстояния  ); определяемые данные – координаты
); определяемые данные – координаты  точки P.
точки P.
Графическое решение.
Сначала на чертеже (плане) нужно построить систему координат и нанести точки Α и Β по их известным координатам; затем нужно соединить точки Α и Β прямой линией, от линии ΑΒ отложить по часовой стрелке угол β и провести линию положения точки P. Зафиксировать на циркуле расстояние S в масштабе чертежа (плана) и провести небольшую дугу радиусом S; точка пересечения линии и дуги является искомой точкой P (рис.28).
 |
Рисунок 28 – Схема полярной засечки
Вычислим дирекционный угол направления АP  и запишем два уравнения, соответствующие двум элементарным измерениям: уравнение прямой линии, проходящей через точку А в заданном направлении АP, и уравнение окружности радисом
и запишем два уравнения, соответствующие двум элементарным измерениям: уравнение прямой линии, проходящей через точку А в заданном направлении АP, и уравнение окружности радисом  с центром в точке А
с центром в точке А
Алгоритм решения полярной засечки в кратком виде:
- вычислить дирекционный угол линии AP  ;
;
- вычислить приращения координат:  ;
;  ;
;
- вычислить координаты точки P:  ;
;  ;
;
- вычислить ошибку положения точки P:  ; ρ=206265”.
; ρ=206265”.
Пример решения полярной засечки приведён в таблице 4.
Таблица 4 - Решение полярной засечки
| № п/п | Обозначения | Вычисления |
| αΑΒ β | 3040 07’ 08” 34 12 30 | |
| 6’ | αΑP αΑP (десятичная форма) | 338 19 38 338. 327 222 |
| Sin αΑP Cos αΑP S (м) | − 0. 369 305 + 0. 929 308 1 000.00 | |
XA (м)

| 6 642 000.00 + 929.31 | |
| XP YP | 6 642 929.31 7 374 630.70 | |
 YA (м)
YA (м)
| − 369.30 7 375 000.00 | |
| MP (м) | 0.17 |
3.3.4. Прямая и обратная геодезические задачи
В геодезии есть две стандартные задачи: прямая геодезичеcкая задача на плоскости и обратная геодезическая задача на плоскости.
Прямая геодезическая задача - это вычисление координат  ,
,  второго пункта, если известны координаты
второго пункта, если известны координаты  ,
,  первого пункта, дирекционный угол
первого пункта, дирекционный угол  и длина
и длина  линии, соединяющей эти пункты.
линии, соединяющей эти пункты.
Прямая геодезическая задача является частью полярной засечки, и формулы для ее решения берутся из набора формул для решения полярной засечки
 ,
,
 .
.
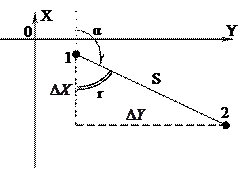 Обратная геодезическая задача - это вычисление дирекционного угла
Обратная геодезическая задача - это вычисление дирекционного угла  и длины
и длины  линии, соединяющей два пункта с известными координатами
линии, соединяющей два пункта с известными координатами  и
и  (рис.29).
(рис.29).
Рисунок 29 – Схема обратной геодезической задачи
Построим на отрезке 1-2 как на гипотенузе прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна  ; катеты равны приращениям координат точек 1 и 2 (
; катеты равны приращениям координат точек 1 и 2 (
 ), а один из острых углов равен румбу
), а один из острых углов равен румбу  линии 1-2.
линии 1-2.
Если  и
и  , то треугольник решается по известным формулам
, то треугольник решается по известным формулам
 ;
;
 и
и 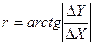 .
.
Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому
 .
.
Общий порядок нахождения дирекционного угла линии 1-2 включает две операции:
- определение номера четверти по знакам приращений координат  ;
;
- вычисление дирекционного угла по формулам связи дирекционного угла и румба в соответствии с номером четверти.
Контролем правильности вычислений является выполнение равенства
 .
.
Если  , то
, то  ,
,
 при
при  ;
;
 при
при 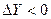 .
.
Если  , то
, то  ,
,
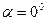 при
при  ;
;
 при
при  .
.
Для решения обратной задачи в автоматическом режиме (в программах для ЭВМ) используется другой алгоритм, не содержащий тангенса угла и исключающий возможное деление на ноль при  :
:
 ,
,
 ,
,
если  , то
, то  ;
;
если 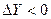 , то
, то 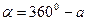 .
.
Таблица 5 – Решение обратной геодезической задачи (1-й алгоритм)
| № п/п | Обозначения | Вычисления |
| XB (м) XA XB – XA | 6 642 841.24 6 642 000.00 + 841.24 | |
| b = (5) / (11) Cos α | 1 499.78 + 0. 560 910 | |
| 8’ | tg r r (десятичная форма) r (IY четверть) α = 3600 – r | 1. 475 952 55. 881 229 550 52’ 52” 3040 07’ 08” |
| Sin α b = (6) / (10) | − 0. 827 877 1 499.78 | |
| YB (м) YA YB − YA | 7 373 758.37 7 375 000.00 − 1 241.63 | |
(XB – XA)2
(YB − YA)2
b2 = (14) + (15)
 b = √ (16) b = √ (16)
| 707 684.7 1 541 645.0 2 249 329.7 1 499.78 |
Таблица 6 – Решение обратной геодезической задачи (2-й алгоритм)
| № п/п | Обозначения | Вычисления |
| XB (м) XA XB – XA | 6 642 841.24 6 642 000.00 + 841.24 | |
| 12’ | Cos a’ = (5) / (10) a’ (десятичная форма) a’ α = 3600 – a’ | + 0. 560 909 55. 881 316 550 52’ 53” 3040 07’ 07” |
| YB (м) YA YB − YA | 7 373 758.37 7 375 000.00 − 1 241.63 | |
(XB – XA)2
(YB − YA)2
b2 = (14) + (15)
 b = √ (16) b = √ (16)
| 707 684.7 1 541 645.0 2 249 329.7 1 499.78 |
3.3.5. Прямая угловая засечка
Сначала рассмотрим так называемый общий случай прямой угловой засечки, когда углы  и
и  измеряются на двух пунктах с известными координатами, каждый от своего направления с известным дирекционным углом (рис.30).
измеряются на двух пунктах с известными координатами, каждый от своего направления с известным дирекционным углом (рис.30).
Исходные данные:  ;
;
Измеряемые элементы:  ;
;
Неизвестные элементы:  точки
точки  .
.
Если  или
или  не заданы явно, нужно решить обратную геодезическую задачу сначала между пунктами A и C и затем между пунктами B и D.
не заданы явно, нужно решить обратную геодезическую задачу сначала между пунктами A и C и затем между пунктами B и D.
Графическое решение. От направления AC отложить с помощью транспортира угол  и провести прямую линию AP; от направления BD отложить угол
и провести прямую линию AP; от направления BD отложить угол  и провести прямую линию BP; точка пересечения этих прямых является искомой точкой P.
и провести прямую линию BP; точка пересечения этих прямых является искомой точкой P.

Рисунок 30 – Общий случай прямой угловой засечки Рисунок 31 – Частный случай ПУЗ
Аналитическое решение. Приведем алгоритм, соответствующий общему случаю засечки:
1) вычислить дирекционные углы линий AP ( ) и BP (
) и BP (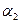 )
)
 ;
;  ;
;
2) написать два уравнения прямых линий
для линии АР  ,
,
для линии ВР  ;
;
3) решить систему двух уравнений и вычислить неизвестные координаты 
 ,
,
 .
.
Частным случаем прямой угловой засечки считают тот случай, когда углы  и
и  измерены от направлений AB и B A, причем угол
измерены от направлений AB и B A, причем угол  - правый, а угол
- правый, а угол  - левый (в общем случае засечки оба угла - левые) - рис.31.
- левый (в общем случае засечки оба угла - левые) - рис.31.
Решение прямой угловой засечки методом треугольника соответствует частному случаю засечки. Порядок решения прямой угловой засечки методом треугольника:
1) решить обратную задачу между пунктами A и B и получить дирекционный угол  и длину
и длину  линии AB,
линии AB,
2) вычислить угол  при вершине P
при вершине P  ;
;
3) используя теорему синусов для треугольника APB
 ,
,
вычислить длины сторон AP ( )и BP (
)и BP ( );
);
4) вычислить дирекционные углы  и
и 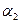
 ,
,  ;
;
5) решить прямую задачу от пункта A к точке P и для контроля - от пункта B к точке P; оба решения должны совпасть.
Для вычисления координат  в частном случае прямой угловой засечки можно использовать формулы Юнга
в частном случае прямой угловой засечки можно использовать формулы Юнга
 ,
,
 .
.
От общего случая прямой угловой засечки нетрудно перейти к частному случаю; для этого нужно сначала решить обратную геодезическую задачу между пунктами A и B и получить дирекционный угол  линии A B и затем вычислить углы в треугольнике APB при вершинах A и B
линии A B и затем вычислить углы в треугольнике APB при вершинах A и B
 и
и 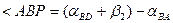 .
.
Для машинного счета все рассмотренные способы решения прямой угловой засечки по разным причинам неудобны. Один из возможных алгоритмов решения общего случая засечки на ЭВМ предусматривает следующие действия:
1) вычисление дирекционных углов  и
и 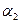 ,
,
|
 с началом в пункте A и с осью
с началом в пункте A и с осью  , направленной вдоль линии AР, пересчет координат пунктов A и B и дирекционных углов
, направленной вдоль линии AР, пересчет координат пунктов A и B и дирекционных углов  и
и 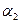 из системы
из системы  в систему
в систему  (рис.32)
(рис.32)
 ;
;  ;
; 
 ;
; 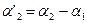 ;
;
 ;
;
 .
.
 |
Рисунок 32 – Прямая угловая засечка в системе координат 
3) запись уравнений линий AP и BP в системе 
 ,
,
 ;
;
и совместное решение этих уравнений
 ,
,
 ; (3.2)
; (3.2)
4) перевод координат  и
и  из системы
из системы  в систему
в систему 
 ,
,
 .
.
Так как  и угол засечки
и угол засечки  всегда больше
всегда больше  , то решение (3.2) всегда существует.
, то решение (3.2) всегда существует.
3.3.6. Линейная засечка
В линейной засечке исходными данными являются координаты пунктов А и В; измеряемыми данными являются расстояния  и
и  (относительная ошибка измерения расстояний
(относительная ошибка измерения расстояний  ); определяемые данные – координаты
); определяемые данные – координаты  точки P.
точки P.
 |
Рисунок 33 – Линейная засечка
Графическое решение.
Сначала на чертеже (плане) нужно построить систему координат и нанести точки Α и Β по их известным координатам; затем нужно провести две окружности с центрами в точках Α и Β, первую окружность – радиусом  и вторую – радиусом
и вторую – радиусом  ; одна из точек пересечения этих окружностей и является искомой точкой Р; другая точка P’ является является вторым (альтернативным) вариантом решением засечки (рис.33)
; одна из точек пересечения этих окружностей и является искомой точкой Р; другая точка P’ является является вторым (альтернативным) вариантом решением засечки (рис.33)
Аналитическое решение линейной засечки может быть выполнено по двум алгоритмам: первый из них предусматривает решение системы уравнений двух измеренных расстояний
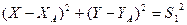 ,
,
 .
.
У этой системы уравнений нет простого решения в системе координат  , поэтому приходится применять систему координат
, поэтому приходится применять систему координат  с началом в точке А и осью
с началом в точке А и осью  , направленной от точки А вдоль линии АВ. В новой системе координаты точек А и В будут равны
, направленной от точки А вдоль линии АВ. В новой системе координаты точек А и В будут равны




Расстояние  , равное длине линии АВ, находится из решения обратной геодезической задачи между точками А и В; при этом вычисляется также дирекционный угол
, равное длине линии АВ, находится из решения обратной геодезической задачи между точками А и В; при этом вычисляется также дирекционный угол  линии АВ.
линии АВ.
Уравнения двух окружностей в новой системе координат  будут иметь вид
будут иметь вид
 ;
;
 .
.
Совместное решение этих двух уравнений предусматривает раскрытие скобок во втором уравнении и вычитание второго уравнения из первого
 ,
,
откуда
 ,
,
и
 .
.
Если искомая точка находится слева от линии АВ, то в формуле для  нужно брать знак “минус”, если справа, то – знак “плюс”.
нужно брать знак “минус”, если справа, то – знак “плюс”.
Пересчёт координат точки  из системы
из системы  в систему
в систему  выполняется по формулам
выполняется по формулам
 ,
,

 .
.
Описанный алгоритм удобен для составления программы при решении линейной засечке на ЭВМ.
Алгоритм “ручного счёта” предусматривает решение треугольника АВР по формулам планиметрии:
- в треугольнике ABР по теореме косинусов вычислить углы β1 и β2
 ,
,
 ;
;
- вычислить угол γ этого же треугольника  ;
;
- вычислить дирекционные углы сторон AР и BР:
точка Р справа от линии AB
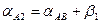 ,
,
 ;
;
точка Р слева от линии AB
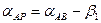 ,
,
 ;
;
дирекционный угол αAB следует взять равным углу α из решения обратной геодезической задачи между точками A и B; 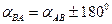 ;
;
- решить прямые геодезические задачи:
из пункта A на точку P
 ,
,
 ,
,
и из пункта B на точку P
 ,
,
 ;
;
расхождение координат  и
и  по двум решениям не должно превышать 0,02 м;
по двум решениям не должно превышать 0,02 м;
- вычислить ошибку положения точки P по формуле
 .
.
Пример решения линейной засечки приведён в таблице 7.
Напоминание: При выполнении операций 19 и 20 искомый угол (β1 или β2) следует перевести из десятичной формы в полную форму, округлить до целых секунд и затем уже записать в таблицу вычислений. Перед выполнением операций 23 и 24 нужно перевести в десятичную форму угол  ; перед выполнением операций 25 и 26 нужно перевести в десятичную форму угол
; перед выполнением операций 25 и 26 нужно перевести в десятичную форму угол  .
.
Таблица 7 - Решение линейной засечки
| № п/п | Обозначения (точка Р справа от линии АВ) | Вычисления |
| b (м) S1 S2 (справа) b2 S12 S22 | 1 499, 78 1 000, 00 1 200, 00 2 249 340 1 000 000 1 440 000 | |
b2 + S12 − S22
 Cos β1 = (13) / (14)
Cos β1 = (13) / (14)
| 1 809 340 2 999 560 + 0, 603 202 | |
| αAB β1 = arcos (15) αAP = (6) + (19) | 3040 07’ 08” 52 54 02 357 01 10 | |
XA (м)
 X2 = (1) + (23)
Y2 = (2) + (24)
X2 = (1) + (23)
Y2 = (2) + (24)
 YA
YA
| 6 643 000, 00 + 998, 65 6 642 998, 65 7 374 948, 00 − 52, 00 7 375 000, 00 | |
b2 + S22 − S12
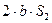 Cos β2 = (16) / (17)
Cos β2 = (16) / (17)
| 2 689 340 3 599 472 + 0, 747 148 | |
| αBA = αAB ± 1800 β2 = arcos (18) αBP = (7) − (20) | 1240 07’ 08” 41 39 22 82 27 46 | |
XB (м)
 X = (3) + (25)
Y = (4) + (26)
X = (3) + (25)
Y = (4) + (26)
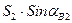 YB
YB
| 6 642 841, 24 + 157, 40 6 642 998, 64 7 374 948, 00 + 1 189, 63 7 373 758, 37 | |

| 850 26’ 36” | |
| MP (м) | 0, 16 |
3.3.7. Обратная угловая засечка
К элементарным измерениям относится и измерение угла  на определяемой точке
на определяемой точке  между направлениями на два пункта
между направлениями на два пункта  и
и 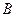 с известными координатами
с известными координатами  и
и  . Однако, это измерение оказывается теоретически довольно сложным, поэтому рассмотрим его отдельно. Проведем окружность через три точки
. Однако, это измерение оказывается теоретически довольно сложным, поэтому рассмотрим его отдельно. Проведем окружность через три точки  . Из школьного курса геометрии известно, что угол с вершиной на окружности измеряется половиной дуги, на которую он опирается. Центральный угол, опирающийся на ту же дугу, измеряется всей дугой, следовательно, он будет равен
. Из школьного курса геометрии известно, что угол с вершиной на окружности измеряется половиной дуги, на которую он опирается. Центральный угол, опирающийся на ту же дугу, измеряется всей дугой, следовательно, он будет равен  (рис.34).
(рис.34).

Рисунок 34 - К вычислению R и координат Ц Рисунок 35 – Обратная угловая засечка
Расстояние  между пунктами
между пунктами  и
и 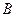 считается известным, и из прямоугольного треугольника
считается известным, и из прямоугольного треугольника  можно найти радиус
можно найти радиус  окружности
окружности
 . (3.3)
. (3.3)
Уравнение окружности имеет вид
 , (3.4)
, (3.4)
где  - координаты центра окружности. Их можно вычислить, решив либо прямую угловую, либо линейную засечку с пунктов
- координаты центра окружности. Их можно вычислить, решив либо прямую угловую, либо линейную засечку с пунктов  и
и 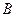 на точку
на точку  . В уравнении (3.4)
. В уравнении (3.4)  - координаты любой точки окружности, в том числе и точки
- координаты любой точки окружности, в том числе и точки  , но для нахождения двух координат точки
, но для нахождения двух координат точки  одного такого уравнения недостаточно. Обратной угловой засечкой называют способ определения координат точки
одного такого уравнения недостаточно. Обратной угловой засечкой называют способ определения координат точки  по двум углам
по двум углам  и
и  , измеренным на определяемой точке
, измеренным на определяемой точке  между направлениями на три пункта с известными координатами
между направлениями на три пункта с известными координатами  (рис.35).
(рис.35).
Исходные данные: 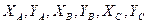 ;
;
Измеряемые элементы:  ;
;
Неизвестные элементы: координаты точки  -
-  .
.
Графическое решение. Приведем способ Болотова графического решения обратной угловой засечки. На листе прозрачной бумаги (кальки) нужно построить углы  и
и  с общей вершиной
с общей вершиной  ; затем наложить кальку на чертеж и, перемещая ее, добиться, чтобы направления углов на кальке проходили через пункты
; затем наложить кальку на чертеж и, перемещая ее, добиться, чтобы направления углов на кальке проходили через пункты  на чертеже; переколоть точку
на чертеже; переколоть точку  с кальки на чертеж.
с кальки на чертеж.
Аналитическое решение. Аналитическое решение обратной угловой засечки предусматривает ее разложение на более простые задачи, например, на две прямые угловые засечки и одну линейную, или на три линейных засечки и т.д. Известно более десяти способов аналитического решения, но мы рассмотрим только один - через последовательное решение трех линейных засечек. Предположим, что положение точки  известно, и проведем две окружности: одну радиусом
известно, и проведем две окружности: одну радиусом  через точки
через точки  и другую - радиусом
и другую - радиусом  через точки
через точки  (рис.35). Радиусы этих окружностей получим по формуле (3.3)
(рис.35). Радиусы этих окружностей получим по формуле (3.3)
 ;
;  .
.
Если координаты центров окружностей (точек  и
и  ) будут известны, то координаты точки
) будут известны, то координаты точки  можно определить по формулам линейной засечки: из точки
можно определить по формулам линейной засечки: из точки  по расстоянию
по расстоянию  и из точки
и из точки  - по расстоянию
- по расстоянию  . Координаты центра
. Координаты центра  можно найти по формулам линейной засечки из точек
можно найти по формулам линейной засечки из точек  и
и 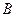 по расстояниям
по расстояниям  , причем из двух решений нужно взять то, которое соответствует величине угла
, причем из двух решений нужно взять то, которое соответствует величине угла  ; если
; если  , то точка
, то точка  находится справа от линии
находится справа от линии  ; если
; если  , то точка
, то точка  находится слева от линии
находится слева от линии  . Координаты центра
. Координаты центра  находятся по формулам линейной засечки из точек
находятся по формулам линейной засечки из точек 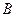 и
и  по расстояниям
по расстояниям  , и одно решение из двух возможных выбирается по тому же правилу: если
, и одно решение из двух возможных выбирается по тому же правилу: если  , то точка
, то точка  находится справа от линии
находится справа от линии  , если
, если  , то точка
, то точка  находится слева от линии
находится слева от линии  .
.
Задача не имеет решения, если все четыре точки  и
и  находятся на одной окружности, так как обе окружности сливаются в одну, и точку их пересечения указать невозможно.
находятся на одной окружности, так как обе окружности сливаются в одну, и точку их пересечения указать невозможно.
1.2.1. Комбинированные засечки
В рассмотренных способах решения засечек количество измерений принималось теоретически минимальным (два измерения), обеспечивающим получение результата, однако, при этом нет контроля правильности измерений. На практике для нахождения координат  и
и  одной точки, как правило, выполняют не два, а три и более измерений; понятно, что в этом случае появляется возможность контроля измерений, и, кроме того, повышается точность решения задачи. Каждое измерение, вводимое в задачу сверх теоретически минимального количества, называют избыточным; оно порождает одно дополнительное решение. Геодезические засечки без избыточных измерений принято называть однократными, а засечки с избыточными измерениями - многократными.
одной точки, как правило, выполняют не два, а три и более измерений; понятно, что в этом случае появляется возможность контроля измерений, и, кроме того, повышается точность решения задачи. Каждое измерение, вводимое в задачу сверх теоретически минимального количества, называют избыточным; оно порождает одно дополнительное решение. Геодезические засечки без избыточных измерений принято называть однократными, а засечки с избыточными измерениями - многократными.
При наличии избыточных измерений вычисление неизвестных выполняют по способу уравнивания. В настоящее время алгоритмы строгого уравнивания измерений в различных геодезических построениях реализованы в машинных программах на ЭВМ; для ручного счета обычно применяют нестрогие (упрощенные) способы уравнивания. Упрощенный способ уравнивания какой-либо многократной засечки ( измерений) предусматривает сначала формирование и решение всех возможных вариантов независимых однократных засечек (их число равно
измерений) предусматривает сначала формирование и решение всех возможных вариантов независимых однократных засечек (их число равно 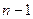 ), а затем - вычисление средних значений координат точки из всех полученных результатов, если они различаются между собой на допустимую величину.
), а затем - вычисление средних значений координат точки из всех полученных результатов, если они различаются между собой на допустимую величину.
1.2.2. Ошибка положения точки в однократных засечках
Положение точки на плоскости по двум измерениям получается в пересечении двух линий положения. Для измеренного расстояния  линией положения является окружность радиуса
линией положения является окружность радиуса  с центром в исходном пункте
с центром в исходном пункте  (рис.36-а); для измеренного угла
(рис.36-а); для измеренного угла  с вершиной в исходном пункте
с вершиной в исходном пункте  - прямая линия, проведенная под углом
- прямая линия, проведенная под углом  к исходной линии
к исходной линии  (рис.36-б).
(рис.36-б).
 |
Рисунок 36 - Линия положения и "полоса положения" точки  :
:
а) для измеренного расстояния, б) для измеренного угла.
Вследствие ошибок измерений необходимо ввести понятие "полоса положения". Для расстояния  , измеренного со средней квадратической ошибкой
, измеренного со средней квадратической ошибкой  - это круговой пояс (кольцо) шириной
- это круговой пояс (кольцо) шириной  между двумя окружностями радиусами
между двумя окружностями радиусами  и
и  ; для угла
; для угла  , измеренного с ошибкой
, измеренного с ошибкой 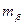 - это узкий треугольник с вершиной в точке
- это узкий треугольник с вершиной в точке  и углом при вершине
и углом при вершине  . Линия положения точки является осью симметрии полосы положения (рис.37).
. Линия положения точки является осью симметрии полосы положения (рис.37).
Введем понятие "вектор ошибки измерения" и обозначим его через 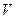 . Для измеренного расстояния вектор
. Для измеренного расстояния вектор  направлен вдоль линии
направлен вдоль линии  (прямо или обратно) и имеет модуль
(прямо или обратно) и имеет модуль  ; для измеренного угла вектор
; для измеренного угла вектор  направлен перпендикулярно линии
направлен перпендикулярно линии  (влево или вправо от нее) и имеет модуль
(влево или вправо от нее) и имеет модуль  , где
, где 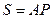 .
.
Точка  , находясь на пересечении двух линий положения, является центром четырёхугольника положения, образующегося в пересечении двух полос положения (рис.37). Этот элементарный четырёхугольник можно считать параллелограммом, так как в пределах него дуги окружностей можно заменить отрезками касательных, а расходящиеся стороны угла - отрезками прямых, параллельных линии положения. Расстояния от точки
, находясь на пересечении двух линий положения, является центром четырёхугольника положения, образующегося в пересечении двух полос положения (рис.37). Этот элементарный четырёхугольник можно считать параллелограммом, так как в пределах него дуги окружностей можно заменить отрезками касательных, а расходящиеся стороны угла - отрезками прямых, параллельных линии положения. Расстояния от точки  до границ четырёхугольника неодинаковы, что говорит о различии ошибок положения точки
до границ четырёхугольника неодинаковы, что говорит о различии ошибок положения точки  по разным направлениям.
по разным направлениям.
 |
Рисунок 37 - Четырёхугольник положения:
а) в линейной засечке, б) в прямой угловой засечке.
Линии положения делят четырёхугольник положения на 4 равные части (рис.38), которые назовем параллелограммами ошибок с углами при вершинах  и
и  , где -
, где - 
 - угол между векторами ошибок
- угол между векторами ошибок  и
и  .
.
 |
|
12 | Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-08-20 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд