Министерство образования и науки Российской Федерации
Кафедра
Пояснительная записка
К курсовой работе:
«Исследование методов вычисления определенных интегралов»
Выполнил: студент гр..
Проверил:.
- 2012
Содержание
1. Теоретическая часть 2
2. Описание программы 8
3. Блок-схемы 15
4. Вывод 16
5. Список литературы 17
Теоретическая часть
Метод прямоугольников
Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида
где f(x) -данная функция, непрерывная на отрезке [a; b]. Если функция f(x) задана формулой и мы умеем найти неопределенный интеграл F(x), то определенный интеграл вычисляется по формуле Ньютона-Лейбница:
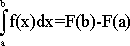
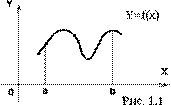
Если же неопределенный интеграл данной функции мы найти не умеем, или по какой-либо причине не хотим воспользоваться формулой Ньютона-Лейбница или если функция f(x) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла можно использовать метод прямоугольников (правых, левых, средних). При вычислении интеграла следует помнить, каков геометрический смысл определенного интеграла. Если f(x)>=0 на отрезке [a; b], то
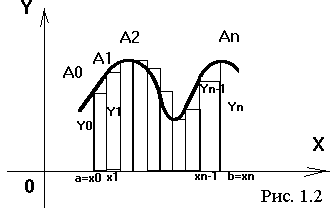
численно равен площади фигуры, ограниченной графиком функции y=f(x), отрезком оси абсцисс, прямой x=a и прямой x=b (рис. 1.1) Таким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции.
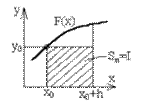
Разделим отрезок [a; b] на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка
.
Точки деления будут: x0=a; x1=a+h; x2=a+2*h,..., xn-1=a+(n-1)*h; xn=b.
Числа y0, y1, y2,..., yn являются ординатами точек графика функции, соответствующих абсциссам x0, x1, x2,..., xn (рис. 1.2).
Строим прямоугольники. Это можно делать несколькими способами:
Левые прямоугольники (слева направо)
Правые прямоугольники (построение справа налево)
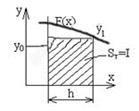
Средние прямоугольники (посередине)
Из рис. 1.2 следует, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.
h=(b-a)/n –ширина прямоугольников
Формула левых прямоугольников:
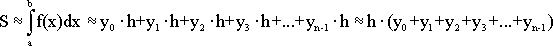(1.3)
Формула правых прямоугольников:
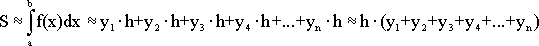(1.4)
Формула средних прямоугольников.
Sсредих= (Sправых + Sлевых) /2
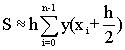(1.5)
Метод Симпсона
Для приближённого вычисления интеграла функции f(x) используются методы приближённого интегрирования, наиболее употребительные из них основаны на замене интеграла конечной суммой. Для вычисления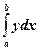 
промежуток от a(x0) до b(xn) разбивается на n равных частей, и для точек деления x0, x1, x2, x3,..., xn-1, xn вычисляются значения интегрируемой функции y. Затем необходимо воспользоваться формулой приближённого интегрирования:
Формула Cимпсона (парабол) (рис.2):
(2)
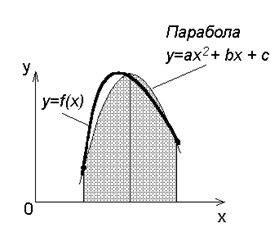
Рис.2.
В курсовой работе рассматривается приближенное вычисление интеграла
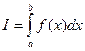(1)
При его аппроксимации заменим функцию f(x) параболой, проходящей через точки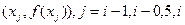 
т.е представим приближенно f(x) в виде:
где 
- интерполяционный многочлен Лагранжа второй степени,
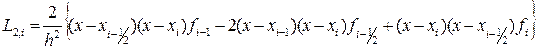. (2)
Проводя интегрирование получим
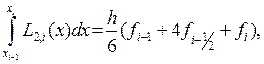
Таким образом приходим к приближенному равенству
(3)
Котрое называется формулой Симпсона или формулой парабол.
На всем отрезке [a,b] формула Симпсона имеет вид
Чтобы не использовать дробных индексов можно обозначить
xi=a+0,5hi, fi=f(xi), i=1,2,…,2N, hN=b-a
и записать формулу Симпсона в виде:
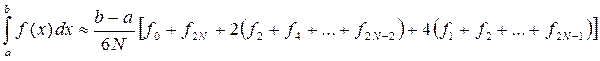(4)
Прежде чем переходить к оценке погрешности формулы (3) заметим, что она является точной для любого многочлена третьей степени, т.е. имеет место точное равенство
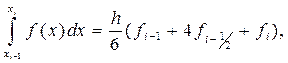
если f(x)=a0+a1x+a2x2+a3x3. Это утверждение нетрудно проверить непосредственно.
Для оценки погрешности формулы Симпсона воспользуемся интерполяционным многочленом Эрмита. Построим многочлен третьей степени H3(x) такой, что
.
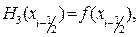
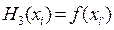Такой многочлен существует и единствен.
Однако нам даже не потребуется явный вид многочлена H3(x). Вспоминая, что формула Симпсона точна для любого многочлена третьей степени, получим
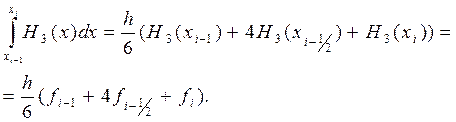(5)
Представим теперь f(x) в виде
f(x)=H3(x)+ri(x), 
xÎ[xi-1,xi], (6)
где ri(x) – погрешность интерполирования многочленом Эрмита H3(x). Интегрируя (6) и учитывая (5), получим
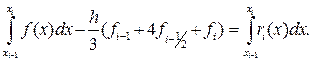(7)
Далее имеем
поэтому из (7) для погрешности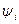 
формулы (3) получаем оценку
где 
Вычисляя интеграл приходим к окончательной оценке
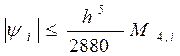(8)
Погрешность составной формулы Симпсона оценивается так
(9)
Отсюда видно, что формула Симпсона существенно точнее, чем формулы прямоугольников и трапеций. На частичном отрезке она имеет точность О(h5), а на всем отрезке – O(h4).
Описание программы
Тело программы.
рис 1. Окно программы до вычислений
Option Explicit
Private Sub Enter_Click()
Form4.Show (1)
End Sub