Пирамидальная сортировка
Пирамидальная сортировка производится с помощью двоичной кучи (отсюда и английское название – heapsort). Этот алгоритм сочетает преимущества сортировки слиянием и сортировки вставками. Он гарантированно (то есть в лучшем, худшем и среднем случаях) работает за время O(n* log n), но при этом требуется меньше дополнительной памяти, чем для сортировки слиянием — O(1) против O(n). Данный метод был предложен Дж. Уильямсом в 1964 году.
Двоичная куча — массив с определёнными свойствами упорядоченности. Чтобы сформулировать эти свойства, будем рассматривать массив как двоичное дерево.
Термином «куча» также обозначают область машинной памяти, где работает автоматическая «сборка мусора», но к данном алгоритму это отношения не имеет.
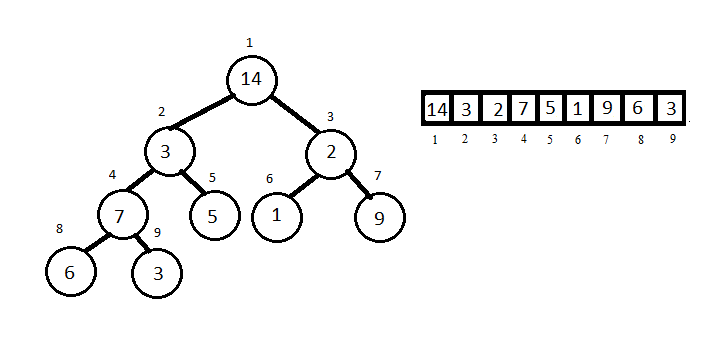 Рис.1: Массив (справа) можно представить в виде двоичного дерева (слева). Чтобы дерево было двоичной кучей, нужно выполнение основного свойства кучи, речь о котором пойдёт ниже.
Рис.1: Массив (справа) можно представить в виде двоичного дерева (слева). Чтобы дерево было двоичной кучей, нужно выполнение основного свойства кучи, речь о котором пойдёт ниже.
Каждая вершина дерева соответствует элементу массива. Если вершина имеет индекс i, то её родитель имеет индекс [i/2] (вершина с индексом 1 является корнем), а её дети — индексы 2i и 2i + 1. Будем считать, что куча может и не занимать всего массива, тогда нужно хранить не только массив A и его длину length_A, но и параметр heap_size_A, причём heap_size_A ≤ length_A.
Таким образом, куча состоит из элементов A[1], …, A[heap_size_A]. Индексирование массивов с нуля, принятое в C, в данном случае неудобно, так как вершина с индексом 0 будет иметь потомков 0 и 1, т.е. нулевой индекс повторится дважды. Это можно обойти, но для удобства в примерах кода на C-подобном языке будем считать, что первый элемент массива имеет индекс 1.
Движение по дереву осуществляется функциями:
int Parent (int i)
{
return (int)(i/2); //(int) возвращает целую часть числа
}
int Left (int i)
{
return 2i;
}
int Right(int i)
{
return (2i + 1);
}
В большинстве компьютеров для выполнения процедур Left и Parent подходят команды левого и правого побитового сдвига (соответствующие умножению и делению числа на 2). Для команды Right потребуется правый сдвиг и помещение единицы в младший разряд полученного числа (прибавление единицы).
Все элементы, хранящиеся в куче, должны обладать основным свойством кучи (англ. heap property): для каждой вершины с номером i, кроме корня (т.е. при 2≤ i ≤ heap_size_A),
A[Parent(i)] ≥ A[i]
То есть значение потомка всегда не превосходит значения предка. Таким образом, наибольший элемент дерева (или любого поддерева) находится в корневой вершине дерева (данного поддерева).
Высотой (height) вершины дерева называется высота поддерева с корнем в этой вершине — число рёбер в самом длинном пути вниз по дереву к листу. Таким образом, высота дерева совпадает с высотой его корня. В дереве, составляющем кучу, все уровни (кроме, быть может, последнего) заполнены полностью. Поэтому высота этого дерева равна O(log n), где n — число элементов в куче. Как будет показано далее, время работы основных операций над кучей пропорционально высоте дерева и, следовательно, составляет O(log n).
Основные операции над кучей:
1) Процедура Heapify позволяет поддерживать основное свойство кучи. Время её работы составляет O(log n).
2) Процедура Build_Heap строит кучу из исходного (неотсортированного) массива. Время работы O(n).
3) Процедура Heapsort сортирует массив, не используя дополнительной памяти. Время работы — O(n *log n).
Сохранение основного свойства кучи
Функция Heapify является важным средством для работы с кучей. Её параметры — массив A и индекс i. Предполагается, что элементы с индексами Left (i) и Right (i) уже обладают основным свойством. Процедура переставляет элементы поддерева с вершиной i, после чего оно будет обладать основным свойством. Это выполняется просто: если основное свойство не выполнено для вершины i, то её следует поменять местами с наибольшим из её потомков, и так далее, пока элемент A[i] не «опустится» до нужного места.
Функция Heapify на языке, подобном C, выглядит следующим образом:
void Heapify (int * A, int i)
{
int largest;
int l = Left (i);
int r = Right (i);
if (l <= heap_size_A && A[l] > A[i])
{
largest = l;
}
else
{
largest = i;
}
if (r <= heap_size_A && A[r] > A[largest])
largest = r;
if (largest!= i)
{
Interchange (A, i, largest);
Heapify(A, largest);
}
}
Здесь процедура Interchange меняет местами два элемента массива Array с индексами index1 и index2:
void Interchange (int * Array, int index1, int index2)
{
int temp_num = Array[index1];
Array[index1] = Array[index2];
Array[index2] = temp_num;
return;
}
Работа процедуры Heapify заключается в следующем. Она выбирает из трёх элементов — вершины i и двух её потомков 2i, 2i+1 — наибольший, и его индекс помещается в переменную largest. Если этот индекс совпадает с i, то данная вершина уже «погрузилась» на нужную глубину в дереве, и работа процедуры завершается. Если же один из потомков оказался больше корня, эти вершины меняются местами, что обеспечивает выполнение основного свойства кучи для вершины i, но может вызвать нарушение его в вершине largest. Поэтому в данном случае процедура Heapify рекурсивно вызывается с параметрами A, largest.
Оценим время работы Heapify. На каждом шаге требуется произвести O(1) действий, не считая рекурсивного вызова. Пусть T(n) — время работы для поддерева, содержащего n элементов. Если поддерево с корнем i состоит из n элементов, то поддеревья с корнями Left (i) и Right (i) содержат не более 2n/3 элементов каждое (наихудший случай — когда последний уровень в поддереве заполнен наполовину). Получаем, что
T(n) ≤ T(2n/3) + O(1)
По основной теореме о рекуррентных соотношениях имеем: T(n) = O(log n). Эту же оценку можно получить так: на каждом шаге мы спускаемся по дереву на один уровень, а высота дерева, как выяснено ранее, равна O(log n).