Окружность — геометрическая фигура, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от данной точки.
Эту точку называют центром окружности, а заданное расстояние — радиусом окружности.
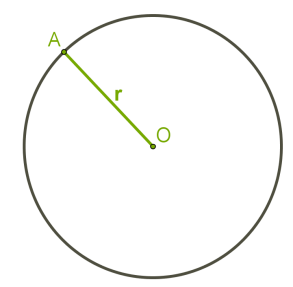
Радиус — это отрезок, соединяющий центр окружности с любой точкой окружности. Из определения следует, что можно провести бесконечное количество радиусов, и они все имеют одинаковую длину.
Отрезок, который соединяет две точки на окружности, называют хордой.
Если хорда проходит через центр окружности, то её называют диаметром окружности.
Диаметр — самая длинная хорда.
В окружности также можно провести бесконечное количество диаметров.
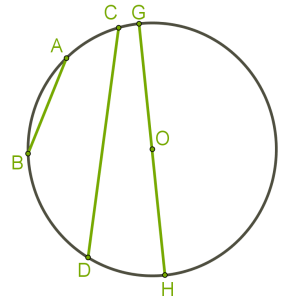
Если соединить две точки окружности не отрезком, а кривой, проходящей по самой окружности, то часть окружности между двумя точками называют дугой.
Если на окружности отметить две точки, то получаются две дуги. Поэтому для названия дуги используют три латинские буквы, которые могут быть как маленькие, так и большие.
На рисунке выше можем назвать: дуга BDH, дуга ACG и другие.
На рисунке ниже нарисованы: дуга AxB и дуга AyB.
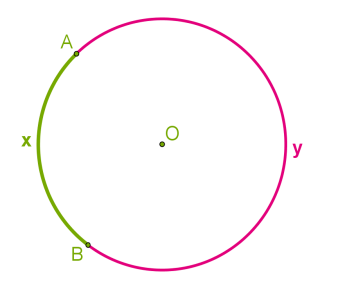
Часть плоскости, ограниченная окружностью, называется кругом.
Задачи на построение

В задачах, где необходимо выполнить конструкции, используются циркуль и линейка.
Очень важно запомнить, что в этих задачах линейка используется не как инструмент для измерения, а исключительно только для того, чтобы провести прямую, луч или отрезок через две данные точки, то есть, чтобы провести прямую линию. Циркуль используется для построения окружности или дуги окружности.
Рассмотрим пять основных построений, в которых используем упомянутые действия — построение прямой линии и окружности:
1. на данном луче от его начала отложить отрезок, равный данному.
2. Построение угла, равного данному.
3. Построение биссектрисы угла.
4. Построение перпендикулярных прямых.
5. Построение середины отрезка.
1. На данном луче от его начала отложить отрезок, равный данному.
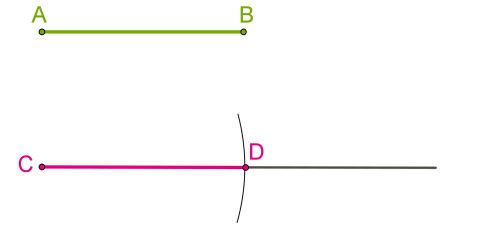
Ясно, что таким образом мы получили отрезок, равный данному. Соответственно определению окружности, она состоит из точек, расположенных на заданном расстоянии (радиусе) от некоей точки (центра окружности).
Если центром служит начальная точка луча C, радиусом — данный отрезок AB, то точка пересечения окружности и луча D и есть искомая конечная точка отрезка CD, равного данному отрезку AB.
2. Построение угла, равного данному.
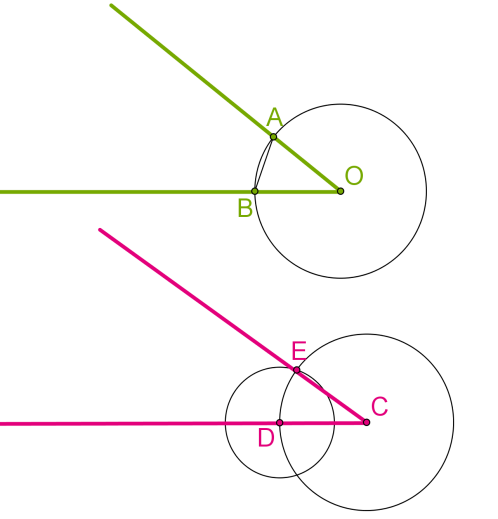
Докажем, что построенный угол ECD и есть тот искомый угол, равный данному углу AOB.
Если мы построили окружность с центром C — начальной точкой луча и таким же радиусом, как у окружности с центром O, то CD = OB.
Если далее мы построили окружность с центром D и радиусом, равным отрезку BA, и получили точку пересечения обеих окружностей E, то BA = DE.
Провели луч CE. Очевидно, OA = CE.
Значит, треугольники AOB и ECD равны по третьему признаку равенства треугольников, у них равны и углы, в том числе угол ECD равен углу AOB.
3. Построение биссектрисы угла.
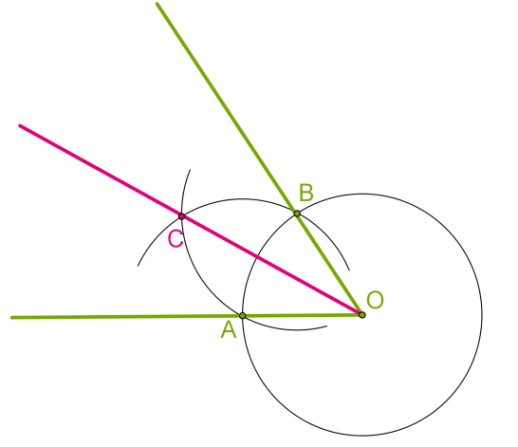
Чтобы доказать, что OC действительно делит угол AOB пополам, достаточно рассмотреть треугольники AOC и BOC.
OA=OB как радиусы одной окружности, а AC=BC, так как мы при построении выбрали одинаковые радиусы для обеих окружностей.
Сторона OC — общая.
Эти треугольники равны по третьему признаку.
Следовательно, их соответствующие углы равны.
Значит, AOC и BOC — две равные части одного угла, это означает, что луч OC делит угол пополам.
4. Построение перпендикулярных прямых.
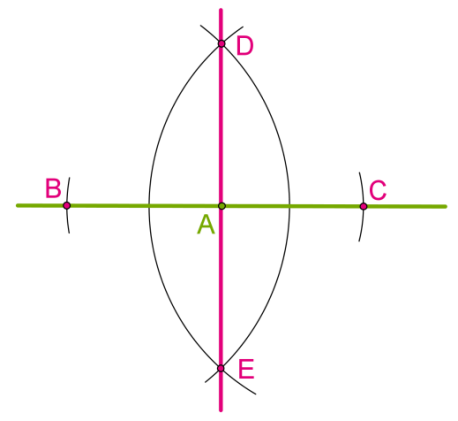
Почему DE является перпендикулярной к BC?
AB=AC — так эти точки были отложены при построении.
BD=CD, так как мы обе окружности построили с одинаковыми радиусами.
Значит, DA или EA — медианы, проведённые к основанию равнобедренных треугольников BDC или BEC.
Медиана в равнобедренном треугольнике является также высотой, то есть перпендикулярна к основанию.
5. Построение середины отрезка.
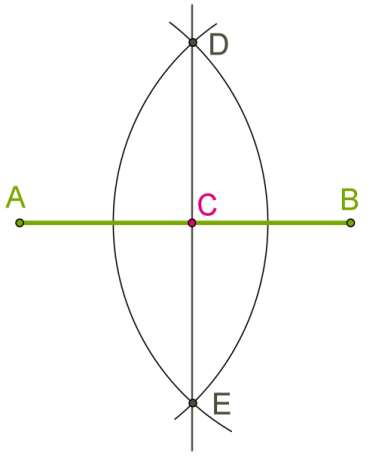
Эта конструкция такая же, как в случае построения перпендикулярных прямых, и уже доказано, что DC или EC делит AB пополам, то есть C — серединная точка отрезка AB.