Страховые услуги
3. Услуги для населения:
§ «КиберПочт@» - на территории Санкт-Петербурга и Ленинградской области действуют ПКД в 237 почтовых отделениях Санкт-Петербурга и в 278 почтовых отделениях Ленинградской области;
§ «КиберПресс@»;
§ распространение печати по подписке;
§ оформление подписки на терминалах самообслуживания;
§ оплата электронных авиабилетов на терминалах самообслуживания;
§ продажа проездных билетов;
§ продажа бестиражных и тиражных лотерей;
§ услуги телефонной связи;
§ «Поздравление от Деда Мороза»;
Подписка на собрание сочинений книжного клуба «Терра»
4. Решения для бизнеса:
§ денежные переводы «КиберДеньги» (для корпоративных клиентов);
§ размещение рекламы (рекламно-информационных материалов в отделениях почтовой связи, наружной рекламы, распространение печатной рекламы);
Директ-мейл и другие
2. Общие сведения о потоках требований.
Потоком требований (событий) называется последовательность однородных требований, появляющихся одно за другим в случайные моменты времени, например, поток вызовов на телефонной станции, прибытие поездов на станцию, поток сбоев ЭВМ, поток заявок на проведение работ в вычислительном центре и т.п.
Потоки требований обладают свойствами стационарности, ординарности и отсутствия последействия. Свойство стационарности означает, что с течением времени вероятностные характеристики потока не меняются. Поток можно назвать стационарным, если для любого числа k требований, поступивших за промежуток времени длиной 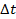 , вероятность поступления требований зависит только от величины промежутка и не зависит от его расположения на оси времени.
, вероятность поступления требований зависит только от величины промежутка и не зависит от его расположения на оси времени.
Свойство ординарности означает практическую невозможность группового поступления требований. Поэтому поток требований можно назвать ординарным тогда, когда вероятность поступления двух или более требований за любой бесконечно малый промежуток времени 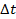 есть величина бесконечно малая более высокого порядка, чем
есть величина бесконечно малая более высокого порядка, чем 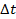 . Свойство отсутствия последействия означает независимость вероятностных характеристик потока от предыдущих событий. Иными словами, вероятность поступления k требований в промежуток [
. Свойство отсутствия последействия означает независимость вероятностных характеристик потока от предыдущих событий. Иными словами, вероятность поступления k требований в промежуток [  ] зависит от числа, времени поступления и длительности обслуживания требований до момента
] зависит от числа, времени поступления и длительности обслуживания требований до момента  .
.
К основным характеристикам случайного потока относят ведущую функцию и интенсивность. Ведущая функция случайного потока  есть математическое ожидание числа требований в промежутке
есть математическое ожидание числа требований в промежутке  . Функция
. Функция  неотрицательная, неубывающая, и в практических задачах теории распределения информации непрерывна и принимает только конечные значения. Интенсивностью λ потока событий называется среднее число (математическое ожидание числа) событий, приходящееся на единицу времени. Для стационарного потока λ = const; для нестационарного потока интенсивность в общем случае зависит от времени: λ = λ(t).
неотрицательная, неубывающая, и в практических задачах теории распределения информации непрерывна и принимает только конечные значения. Интенсивностью λ потока событий называется среднее число (математическое ожидание числа) событий, приходящееся на единицу времени. Для стационарного потока λ = const; для нестационарного потока интенсивность в общем случае зависит от времени: λ = λ(t).
3. Классификация потоков требований.
Простейшие потоки.
Если поток требований обладает свойствами стационарности, ординарности и отсутствия последствия, то такой поток называется простейшим (или пуассоновским) потоком требований.
Вероятность поступления k требований за промежуток времени t в пуассоновском потоке определяется из выражения:

Интервал времени T между двумя соседними событиями простейшего потока имеет показательное распределение:

где  – величина, обратная среднему значению интервала T.
– величина, обратная среднему значению интервала T.
Математическое ожидание, дисперсия и среднеквадратическое отклонение промежутка T:



Полученное совпадение величин M и σ характерно для показательного распределения. Это свойство на практике используют как критерий для первоначальной проверки соответствия гипотезы о показательном распределении полученным статистическим данным.
Простейший поток с возможной нестационарностью. Простейшим потоком с возможной нестационарностью (нестационарным простейшим потоком) является поток, обладающий свойствами ординарности, отсутствием последействия и имеющий в каждый момент времени t конечное мгновенное значение параметра λ(t).
Мгновенная интенсивность нестационарного простейшего потока λ(t) определяется как предел отношения среднего числа событий, которые произошли за элементарный интервал времени ( ), к длине
), к длине 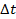 этого интервала, когда
этого интервала, когда 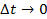 . Среднее число событий, наступающих в интервале времени
. Среднее число событий, наступающих в интервале времени 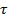 , следующем непосредственно за моментом
, следующем непосредственно за моментом  , равно:
, равно:

Если поток событий стационарный, то:

Тогда вероятность наступления k требований для рассматриваемого вида потока будет равна:
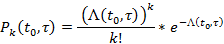
Простейший поток с возможной неординарностью. Простейший поток с возможной неординарностью обладает свойствами стационарности и отсутствием последействия. Требования в таком потоке могут поступать не по одному, а сразу группами (пакетами). В этом случае все требования, приходящие одновременно, объединяются в пакеты, вероятность поступления двух или более числа пакетов за промежуток времени t, есть величина, бесконечно малая по отношению к t. Каждый пакет, исходя из определения, содержит хотя бы одно требование.
Вероятность поступления k требований для потока с возможной неординарностью с учетом вероятности  нахождения m требований в пакете:
нахождения m требований в пакете:

Простейшие потоки с возможным последействием. Поток, имеющий конечное значение параметра и обладающий свойствами стационарности и ординарности, является простейшим потоком с возможным последействием. Условная вероятность поступления некоторого числа требований на заданном промежутке времени t такого потока вычисляется при предположении о предыстории потока (о поступлении требований до этого промежутка времени) и может отличаться от безусловной вероятности того же события.
Вероятность поступления требований k за данный промежуток времени t для потока с возможным последействием будет выглядеть следующим образом:

где  функция Пальма-Хинчина.
функция Пальма-Хинчина.
Функция  представляет собой вероятность поступления k требований за время t при условии, что в начальный момент этого промежутка t поступает хотя бы одно (а в силу ординарности потока ровно одно) требование (это начальное требование не входит в число k требований за время t).
представляет собой вероятность поступления k требований за время t при условии, что в начальный момент этого промежутка t поступает хотя бы одно (а в силу ординарности потока ровно одно) требование (это начальное требование не входит в число k требований за время t).
Потоки Пальма. Ординарный поток событий называется потоком Пальма (или рекуррентным потоком, или потоком с ограниченным последействием), если интервалы времени  между последовательными событиями представляют собой независимые, одинаково распределенные случайные величины.
между последовательными событиями представляют собой независимые, одинаково распределенные случайные величины.
В связи с одинаковостью распределений  поток Пальма всегда стационарен.
поток Пальма всегда стационарен.
Простейший поток является частным случаем потока Пальма; в нем интервалы между событиями распределены по показательному закону.
Потоки Эрланга. Потоком Эрланга n -го порядка называется поток событий, получающийся «прореживанием» простейшего потока, когда сохраняется каждая n -я точка (событие) в потоке, а все промежуточные выбрасываются.
Интервал времени между двумя соседними событиями в потоке Эрланга n -го порядка представляет собой сумму n независимых случайных величин  , имеющих показательное распределение с параметром
, имеющих показательное распределение с параметром  :
:

Закон распределения случайной величины T называется законом Эрланга n -го порядка и имеет плотность:

Математическое ожидание, дисперсия и среднеквадратическое отклонение случайной величины T соответственно равны:

Для потоков Эрланга n -го порядка вероятность поступления k требований за промежуток времени t равняется:

При k = 0:

Суммирование и разъединение простейших потоков. При объединении нескольких независимых простейших потоков образуется также простейший поток с параметром, равным сумме параметров исходных потоков. Разъединение поступающего простейшего потока с параметром λ на n направлений происходит так, что каждое требование исходного потока с вероятностью 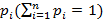 поступает на i -ое направление, а поток на i -го направления также будет простейшим с параметром
поступает на i -ое направление, а поток на i -го направления также будет простейшим с параметром  . Эти свойства простейшего потока широко используются на практике, поскольку значительно упрощают расчёты стационарного оборудования и информационных сетей.
. Эти свойства простейшего потока широко используются на практике, поскольку значительно упрощают расчёты стационарного оборудования и информационных сетей.
Показательный закон распределения времени обслуживания. Временем обслуживания называется время, затрачиваемое каждым узлом обслуживания на одно требование.
Время обслуживания характеризует пропускную способность каждого узла обслуживания, не связано с оценкой качества обслуживания и является случайной величиной.
Это объясняется неидентичностью узлов обслуживания и различием в спросе на обслуживание отдельных требований. Например, поступающие на ремонт вагоны имеют неисправности самого различного характера, попадают в различные ремонтные бригады, поэтому время на обслуживание для различных вагонов не будет одинаковым.
Во многих задачах теории массового обслуживания закон распределения времени обслуживания предполагается показательным и описывается выражением:
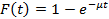
Параметр  характеризует среднюю скорость обслуживания требований.
характеризует среднюю скорость обслуживания требований.
4. Классификация систем массового обслуживания.
Системы массового обслуживания (далее СМО) – системы, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо видов услуг, а, с другой стороны, происходит удовлетворение этих запросов.
СМО включает в себя следующие элементы:
· источник требований;
· входящий поток требований;
· очередь;
· обслуживающее устройство (обслуживающий аппарат, канал обслуживания);
· выходящий поток требований.
СМО классифицируют по разным признакам. Одним из признаков является ожидание требования начала обслуживания. В соответствии с этим признаком системы подразделяются на следующие виды:
1) СМО с потерями (отказами);
2) СМО с ожиданием;
3) СМО с ограниченной длиной очереди;
4) СМО с ограниченным временем ожидания.
Системы с потерями или отказами - СМО, у которых требования, поступающие в момент, когда все приборы обслуживания заняты, получают отказ и теряются.
Системы с ожиданием – СМО, у которых, возможно появление как угодно длинной очереди требований к обслуживающему устройству.
Системы с ограниченной длиной очереди – СМО, допускающие очереди, но с ограниченным числом мест в ней.
Системы с ограниченным временем ожидания – СМО, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней.
По числу каналов обслуживания СМО делятся на:
1. одноканальные;
2. многоканальные.
По месту нахождения источника требований СМО делятся на:
1) разомкнутые, т.е. когда источник находится вне системы;
2) замкнутые, т.е. когда источник находится в самой системе.
К последнему виду относится, например, станочный участок, в котором станки являются источником неисправностей, а, следовательно, и требований на их обслуживание.
Одной из форм классификации СМО является кодовая (символьная) классификация Д.Кендалла. При этой классификации характеристику системы записывают в виде трёх, четырёх или пяти символов, например A | B | S, где:
A – тип распределения входящего потока требований;
B – тип распределения времени обслуживания;
S – число каналов обслуживания.
Для экспоненциального распределения принимают символ М, для любого (произвольного) распределения – символ G. Запись M | M | 3 означает, что входящий поток требований – пуассоновский (простейший), время обслуживания распределено по экспоненциальному закону, в системе имеется три канала обслуживания.
Четвёртый символ указывает допустимую длину очереди, а пятый – порядок отбора (приоритета) требований.
5. Характеристики систем массового обслуживания.
Одной из важнейших характеристик обслуживающих устройств, которая определяет пропускную способность всей системы, является время обслуживания.
Время обслуживания одного требования ( ) – случайная величина, которая может изменяться в большом диапазоне. Она зависит от стабильности работы самих обслуживающих устройств, так и от различных параметров, поступающих в систему, требований (к примеру, различной грузоподъемности транспортных средств, поступающих под погрузку или выгрузку).
) – случайная величина, которая может изменяться в большом диапазоне. Она зависит от стабильности работы самих обслуживающих устройств, так и от различных параметров, поступающих в систему, требований (к примеру, различной грузоподъемности транспортных средств, поступающих под погрузку или выгрузку).
Случайная величина  полностью характеризуется законом распределения, который определяется на основе статистических испытаний.
полностью характеризуется законом распределения, который определяется на основе статистических испытаний.
На практике чаще всего принимают гипотезу о показательном законе распределения времени обслуживания.
Показательный закон распределения времени обслуживания имеет место тогда, когда плотность распределения резко убывает с возрастанием времени t. Например, когда основная масса требований обслуживается быстро, а продолжительное обслуживание встречается редко. Наличие показательного закона распределения времени обслуживания устанавливается на основе статистических наблюдений.
При показательном законе распределения времени обслуживания вероятность  события, что время обслуживания продлиться не более чем t, равна:
события, что время обслуживания продлиться не более чем t, равна:

где v - интенсивность обслуживания одного требования одним обслуживающим устройством, которая определяется из соотношения:

где  – среднее время обслуживания одного требования одним обслуживающим устройством.
– среднее время обслуживания одного требования одним обслуживающим устройством.
Следует заметить, что если закон распределения времени обслуживания показательный, то при наличии нескольких обслуживающих устройств одинаковой мощности закон распределения времени обслуживания несколькими устройствами будет также показательным:

где n – количество обслуживающих устройств.
Важным параметром СМО является коэффициент загрузки  , который определяется как отношение интенсивности поступления требований λ к интенсивности обслуживания v.
, который определяется как отношение интенсивности поступления требований λ к интенсивности обслуживания v.

где  – коэффициент загрузки;
– коэффициент загрузки;
λ – интенсивность поступления требований в систему;
v – интенсивность обслуживания одного требования одним обслуживающим устройством.
Из (1) и (2) получаем, что

Учитывая, что λ – интенсивность поступления требований в систему в единицу времени, произведение  показывает количество требований, поступающих в систему обслуживания за среднее время обслуживания одного требования одним устройством.
показывает количество требований, поступающих в систему обслуживания за среднее время обслуживания одного требования одним устройством.
Для СМО с ожиданием количество обслуживаемых устройств n должно быть строго больше коэффициента загрузки (требование установившегося или стационарного режима работы СМО):

В противном случае число поступающих требований будет больше суммарной производительности всех обслуживающих устройств, и очередь будет неограниченно расти.
Для СМО с отказами и смешанного типа это условие может быть ослаблено, для эффективной работы этих типов СМО достаточно потребовать, чтобы минимальное количество обслуживаемых устройств n было не меньше коэффициента загрузки
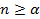
6. Задание на курсовой проект.
Целью настоящего курсового проекта является исследование логистики систем почтовой связи с применением теории массового обслуживания. В раках исследования рассматривается многоканальная система массового обслуживания с ожиданием и ограничением на длину очереди. Данная СМО описываете простейшее отделение почтовой связи, в котором все окна оказывают одинаковые услуги, а длина очереди не имеет зависимости от времени. При исследовании системы определяется влияние изменений различных факторов на показатели функционирования по математической модели. Характеристики системы массового обслуживания приведены в таблице № 1.
Таблица №1:
Параметры, характеризующие рассматриваемую СМО.
| Наименование параметра | Обозначение параметра | Значение параметра по варианту |
| Число каналов | 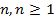
| 
|
| Интенсивность входящего потока каналов | 
| 
|
| Производительность каждого канала | 
| 
|
| Максимальная длина очереди | 
| 
|
1. Пояснения
Число каналов – общее количество каналов в системе массового обслуживания.
Интенсивность входного потока заявок – число заявок, приходящих с СМО. В единицу времени, считаем, что заявки поступают в систему непрерывно, т.е. параметр не зависит от времени. Если канал (оператор) свободен, он берет данную заявку на обслуживание, если канал (оператор) занят, заявка становиться в очередь на обслуживание.
Производительность канала – интенсивность простейшего «потока обслуживания», среднее число заявок, обслуживаемое одним каналом за единицу времени при непрерывной его работе без простоя.
2.Характеристики функционирования рассматриваемой СМО
· Коэффициент нагрузки СМО (трафик): 
· Коэффициент нагрузки на 1 канал: 
· Вероятность простаивания всей системы:


· Вероятности состояний каждого канала:


· Вероятность отказа заявки:

· Вероятность того, что пришедшая заявка будет обслужена:

· Относительная пропускная способность:

· Абсолютная пропускная способность:

· Среднее число занятых каналов:

· Среднее число заявок в очереди:

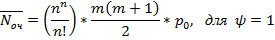
· Среднее число заявок, находящихся в системе:

· Среднее время ожидания заявки в очереди:
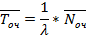
· Среднее время ожидания заявки в системе:

· Среднее время обслуживания одной заявки (как обслуженной, так и не обслуженной):
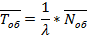
7. Теоретический расчет.
а) при 
Коэффициент нагрузки СМО (трафик):

Коэффициент нагрузки на 1 канал:

Вероятность простаивания всей системы:
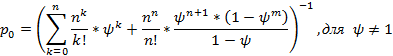


Вероятности состояний каждого канала:


Вероятность состояний первого канала:

Вероятность состояний второго канала:

Вероятность состояний третьего канала:

Вероятность состояний четвертого канала:

Вероятность состояний пятого канала:

Вероятность отказа заявки:

Вероятность того, что пришедшая заявка будет обслужена:
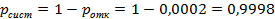
Относительная пропускная способность:

Абсолютная пропускная способность:

Среднее число занятых каналов:
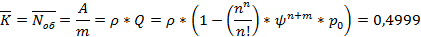
Среднее число заявок в очереди:



Среднее число заявок, находящихся в системе:

Среднее время ожидания заявки в очереди:

Среднее время ожидания заявки в системе:
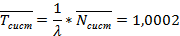
Среднее время обслуживания одной заявки (как обслуженной, так и не обслуженной):

Аналогично рассчитывается для остальных 
Таблица №2:
Вероятность простаивания и вероятность состояний первого канала.

| 
| 
| 
| 
| 
|
| 0,1 | 0,1 | 0,025 | |||
| 0,1 | 0,0905 | ||||
| 0,005 | 0,0045 | ||||
| 0,0002 | 0,0002 | ||||
| 0,4167*10-5 | 0,377*10-5 | ||||
| 0,9425*10-7 |
Таблица №3:
Вероятность простаивания и вероятность состояний второго канала.

| 
| 
| 
| 
| 
|
| 0,2 | 0,2 | 0,05 | |||
| 0,2 | 0,1637 | ||||
| 0,02 | 0,0,163 | ||||
| 0,0013 | 0,0011 | ||||
| 0,6667*10-5 | 0,5458*10-4 | ||||
| 0,2729*10-5 |
Таблица №4:
Вероятность простаивания и вероятность состояний третьего канала.

| 
| 
| 
| 
| 
|
| 0,3 | 0,3 | 0,075 | |||
| 0,1 | 0,2222 | ||||
| 0,3 | 0,0333 | ||||
| 0,045 | 0,0033 | ||||
| 0,0003 | 0,0003 | ||||
| 0,1875*10-4 |
Таблица №5:
Вероятность простаивания и вероятность состояний четвертого канала.

| 
| 
| 
| 
| 
|
| 0,4 | 0,4 | ||||
| 0,4 | 0,2681 | ||||
| 0,08 | 0,0536 | ||||
| 0,0107 | 0,0072 | ||||
| 0,0011 | 0,0007 | ||||
| 0,715*10-4 |
Таблица №6:
Вероятность простаивания и вероятность состояний пятого канала.

| 
| 
| 
| 
| 
|
| 0,5 | 0,5 | 0,125 | |||
| 0,5 | 0,3033 | ||||
| 0,125 | 0,0758 | ||||
| 0,0208 | 0,0126 | ||||
| 0,0026 | 0,0016 | ||||
| 0,0002 |
Таблица №7:
Сводная таблица теоретических расчетов.

| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |

| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |

| 0,025 | 0,05 | 0,075 | 0,1 | 0,125 |

| 0,904 | 0,8187 | 0,7408 | 0,6703 | 0,6065 |

| 0,9425*10-7 | 0,2729*10-6 | 0,1875*10-4 | 0,715*10-4 | 0,0002 |

| 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9998 |

| 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9998 |

| 0,0999 | 0,1999 | 0,2999 | 0,3999 | 0,4999 |
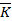
| 0,0999 | 0,1999 | 0,2999 | 0,3999 | 0,4999 |
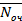
| 0,9425*10-7 | 0,2729*10-6 | 0,1875*10-4 | 0,715*10-4 | 0,0002 |

| 0,1 | 0,2 | 0,3 | 0,4 | 0,5001 |

| 0,9425*10-6 | 0,1365*10-5 | 0,625*10-4 | 0,0002 | 0,0004 |

| 1,0002 | ||||

| 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9998 |
8. Графики.
а) основные показатели системы
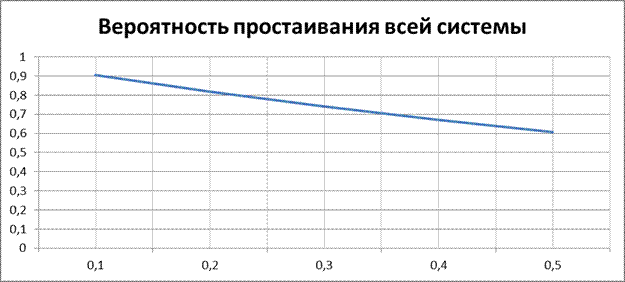

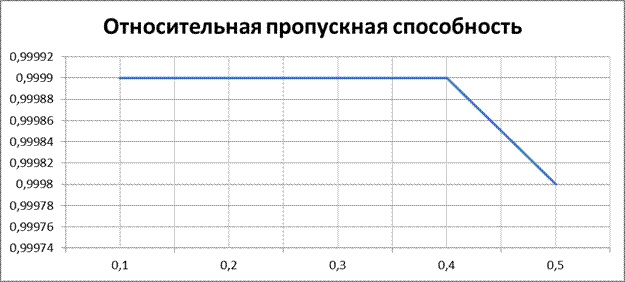


Б) среднее число заявок

