Содержание
Введение
1. Стратегии компенсаций и стратегии исключения при многокритериальном выборе. Метод Франклина
2. Приёмы решения многокритериальных задач
Заключение
Список использованной литературы
Введение
В условиях рыночных отношений выбор технологий, методов анализа, прогнозирования, оптимизации и экономического обоснования управленческого решения финансирует инвестор. "Кто платит, тот и музыку заказывает". В этих условиях не существуют обязательные для всех стандарты или методы управления. Чем выше обоснованность применяемых в конкретной ситуации методов управления и качество управленческого решения, тем меньше коммерческий риск инвестора.
Если при разработке управленческого решения менеджер и его команда не спрогнозировали достаточно точно стратегию фирмы, нормативы конкурентоспособности будущего товара, изменения компонентов внешней и внутренней среды фирмы, то завтра она окажется под угрозой банкротства.
"Будущее начинается сегодня". Поэтому экономия на качестве управленческого решения принесет в будущем огромные потери из-за реализации и тиражирования некачественного решения на последующих стадиях жизненного цикла объекта. В подтверждение этого положения приведем соотношение из американской практики менеджмента - 1: 10: 100: 1000, где "1" - экономия, полученная на стадии маркетинга и научно - исследовательских работ за счет игнорирования современных методов анализа, прогнозирования, оптимизации и экономического обоснования управленческих решений; "10" - потери на стадии проектно-конструкторских и технологических работ; "100" - потери на стадии производства (материализации) объекта; "1000" - потери в сфере потребления данных объектов.
|
|
Качество и эффективность управленческих решений являются основным фактором рационального использования ресурсов и повышения качества товаров.
Принимая управленческое решение, человек обращает внимание на ряд факторов, которые следует учитывать при принятии решения. Чем таких факторов (критериев) больше, тем сложнее принять решение. В реальном мире человеку приходится учитывать множество факторов, то есть перед лицом лица, принимающим управленческое решение, встает задача многокритериального выбора.
В данной работе мы рассмотрим две основные группы стратегий при многокритериальном выборе: стратегии компенсации и стратегии исключения.
Стратегии компенсаций и стратегии исключения при многокритериальном выборе. Метод Франклина
В практической деятельности человека многокритериальные задачи встречаются все чаще, что вызвано усложняющейся ситуацией в принятии решений, когда становится необходимым учитывать много различных факторов. Согласно данным многочисленных исследований существуют две основные группы стратегий, используемых людьми в задачах многокритериального выбора - стратегии компенсации и стратегии исключения.
Стратегии компенсации состоят в том, что консультанты-аналитики стремятся сопоставить оценки одной альтернативы с оценками другой одним из следующих "возможных" способов (стратегий):
· определение полезностей каждой из альтернатив (т.е. выявление предпочтений), а затем их сравнение (стратегия аддитивной модели);
|
|
· сравнение полезностей оценок альтернатив по каждому критерию отдельно, затем суммирование этих разностей (модель аддитивных разностей);
· сравнение достоинств и недостатков одной и той же альтернативы при вербальном анализе, или компенсация по методу Б. Франклина.
Метод Б. Франклина (метод компенсации достоинств и недостатков) основан на идее компромисса между противоречивыми оценками по двум или большему числу критериев. Идея принадлежит Б. Франклину. Он отмечал, что при сравнении трудно одновременно держать в голове все достоинства и недостатки каждой из альтернатив. Поэтому он вписывал в два отдельных списка достоинства и недостатки альтернатив. И после тщательного анализа определял, какой недостаток (или их совокупность) можно считать эквивалентным определенному достоинству (или их совокупности) этой же альтернативы, после чего вычеркивал их из списка. Б. Франклин назвал этот способ "нравственной алгеброй".
Основу систем компенсации составляют процедуры поиска удовлетворительных значений критериев. Эти процедуры также предназначены для систематического поиска наилучшего решения. Однако такой поиск осуществляется по-иному: в порядке очереди определяется приемлемое значение по каждому из критериев.
Примером человекомашинных процедур (ЧМП) поиска удовлетворительных значений критериев служит процедура STEM - одна из первых ЧМП. Она предназначена для решения многокритериальных задач линейного программирования, одной из которых является многокритериальная транспортная задача.
|
|
Рассмотрим фазы расчетов и анализа ЧМП STEM.
Фаза расчетов
1. Проводится оптимизация по каждому критерию отдельно, при этом значения всех остальных критериев заносятся в табл.1.
Таблица 1
Относительные значения критериев
В таблице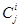 
- значение i-го критерия при оптимизации по j-му критерию. Ясно, что диагональные элементы равны единице, а все прочие меньше единицы. Очевидно, что после нормирования наибольшее значение каждого критерия равно единице, а наименьшее - нулю. Любой столбец содержит значения соответствующего критерия, достигаемые при оптимизации по всем критериям.
В таблице представлена ценная информация, характеризующая область допустимых значений. Так, если значения каких-то двух столбцов близки для каждой из строк (кроме строк, содержащих единицы в этих столбцах), то два соответствующих критерия сильно зависимы, так как изменения всех иных критериев (кроме этих двух) одинаково влияют на эти два критерия. Можно выявить также и противоречивые критерии: высокая оценка по одному сопровождается низкой оценкой по другому. Такая информация весьма полезна для лица, принимающего решения (ЛПР), изучающего возможности, предоставляемые областью D допустимых значений.
2. По табл.1 вычисляются индексы критериев.
Пусть 
- среднее значение, взятое по всем элементам i-ro столбца (кроме единицы). Тогда 
(индекс i-ro критерия) вычисляется из соотношений:
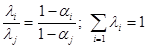
Индекс критериев может быть назван коэффициентом внимания, которое следует уделять критерию при поиске решения.
Предположим, что все элементы i-ro столбца в табл.1 близки к единице. Тогда среднее значение тоже близко к единице, (
) мало и соответствующий индекс мал. Действительно, если при оптимизации по другим критериям значение данного критерия близко к наилучшему, то ему вряд ли стоит уделять внимание.
Наоборот, критерию, сильно зависящему от изменений других критериев ( мало), должны соответствовать большие значения индекса. Индексы называют иногда техническими весами потому, что в отличие от весов 
они не назначаются лицом ЛПР, а вычисляются.
. Производится оптимизация по глобальному критерию.
Глобальный критерий имеет вид:
,
где определяются из предыдущей формулы.
Решение, найденное при оптимизации, предъявляется ЛПР.
Фаза анализа
. ЛПР анализирует вектор значений критериев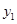 
, найденный при оптимизации по критерию 
. Затем ему задается вопрос: все ли компоненты вектора 
имеют удовлетворительные значения? Если да, то решение получено. Если нет, то ЛПР указывает один критерий с наименее удовлетворительным значением.
. ЛПР просят назначить для критерия с наименее удовлетворительным значением пороговое значение 
, при достижении которого можно признать этот критерий имеющим удовлетворительное значение: 
.
Условие добавляется к совокупности линейных равенств и неравенств, определяющих область D допустимых значений переменных. Таким образом, возникает уже новая область допустимых значений.
На этом фаза анализа заканчивается. Следующий шаг начинается с фазы расчетов при новой области допустимых значений и т.д.
При достижении удовлетворительных для ЛПР значений по всем критериям ЧМП останавливается.