Бинарная классификация
тема
Методы исследований и интеллектуального анализа в программной инженерии
дисциплина
Преподаватель М.Н. Фаворская
подпись, дата
Обучающийся МПИ19-01, 191261007 А.Р. Морозова
номер группы, зачетной книжки подпись, дата
Красноярск 2019
Цель работы
Написать программный модуль, реализующий некоторый алгоритм бинарной классификации.
Теоретическая часть
Одним из существующих подходов, позволяющих реализовать алгоритм бинарной классификации является Линейный дискриминантный анализ (Linear discriminant analysis, LDA).
Этот метод представляет собой обобщение линейного дискриминанта Фишера, используемого в статистике, в сфере распознавания образов и машинного обучения для поиска линейной комбинации признаков. Такой классификатор способен описывать или разделять два и более классов объектов.
В основе дискриминантного анализа лежит предположение о том, что описания объектов каждого -го класса представляют собой реализации многомерной случайной величины, распределенной по нормальному закону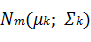 
со средними 
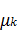и ковариационной матрицей (формула 1), причем индекс 
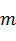указывает на размерность признакового пространства.
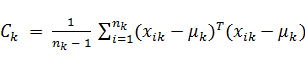(1)
Для случая бинарной классификации можно рассмотреть упрощенную ситуацию, при которой дискриминантные переменные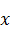 
являются осями
-мерного евклидова пространства. Каждый объект является точкой этого пространства с координатами, представляющими собой фиксируемые значения каждой переменной. Если оба класса отличаются по характеристикам, то их можно представить в виде скоплений точек в разных, возможно частично пересекающихся областях рассматриваемого пространства.
Задача дискриминантного анализа заключается в проведении дополнительной оси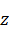 
, проходящей через облако точек так, что проекции на нее обеспечивают наилучшую разделяемость на два класса. Ее положение задается линейной дискриминантной функцией (формула 2) с весовыми коэффициентами 
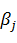, определяющими вклад каждой исходной переменной 
.
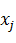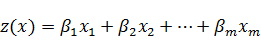(2)
Таким образом, метод линейного дискриминантного анализа можно применить к задаче бинарной классификации.
Практическая часть
В ходе выполнения лабораторной работы был разработан модуль бинарной классификации, использующий метод линейного дискриминантного анализа для предсказания цвет кожи людей на основании их общих характеристик.
Для реализации бинарного классификатора был выбран объектно-ориентированный язык программирования R, широко используемый для статистического анализа, и специально разработанная для него среда программирования RStudio. Как R, так и RStudio доступны для всех операционных систем и являются свободным программным обеспечением. Язык R включает самые последние методики обработки данных и имеет длинный список функций и пакетов, постоянно пополняющийся пользователями языка.
Перед непосредственной реализацией классификатора и дальнейшей с ним работой необходимо подключить несколько библиотек.
> library(MASS)
> library(caret)
> library(ggplot2)
Загрузим данные из файла. В данной программе использовался набор данных об арестах людей различного возраста, пола, цвета кожи и др.
> dataset <- read.csv("Arrests.csv")
> columns <- c("year", "colour", "age", "sex", "employed", "citizen", "checks")
> dataset <- dataset[columns]
Посмотрим, какие характеристики содержит полученный набор данных, и что он в целом представляет из себя внутри.
> dataset
year colour age sex employed citizen checks
1 2002 White 21 Male Yes Yes 3
2 1999 Black 17 Male Yes Yes 3
3 2000 White 24 Male Yes No 0
4 2001 Black 46 Male Yes Yes 1
5 1999 Black 27 Female Yes Yes 1
6 1998 Black 16 Female Yes Yes 0
7 1999 White 40 Male No Yes 0
8 1998 White 34 Female Yes Yes 1
9 2000 Black 23 Male Yes Yes 4
10 2001 White 30 Male Yes Yes 3
Теперь выведем обобщенную информацию об этом наборе, в том числе граничные значения каждой из характеристик и размерность набора данных.
> summary(dataset)
year colour age sex employed citizen
Min.:1997 Black:1288 Min.:12.00 Female: 443 No:1115 No: 771
1st Qu.:1998 White:3938 1st Qu.:18.00 Male:4783 Yes:4111 Yes:4455
Median:2000 Median:21.00
Mean:2000 Mean:23.85
3rd Qu.:2001 3rd Qu.:27.00
Max.:2002 Max.:66.00
checks
Min.:0.000
1st Qu.:0.000
Median:1.000
Mean:1.636
3rd Qu.:3.000
Max.:6.000
> dim(dataset)
[1] 5226 7
Необходимо перемешать данные и разделить их на две части: первая нужна для обучения бинарного классификатора, а вторая – для его тестирования.
> rows <- sample(nrow(dataset))
> dataset <- dataset[rows, ]
> training.samples <- createDataPartition(dataset$sex, p=0.8, list=FALSE)
> train.data <- dataset[training.samples, ]
> test.data <- dataset[-training.samples, ]
Далее нормализуем полученные наборы данных.
> normalizing.param <- preProcess(train.data, method = c("center", "scale"))
> train.transformed <- predict(normalizing.param, train.data)
> test.transformed <- predict(normalizing.param, test.data)
Теперь приступим к обучению классификатора методом линейного дискриминантного анализа. Есть возможность задать вероятности распределения классов с помощью параметра prior.
> LDAmodel <- lda(formula=colour~., data=train.transformed, prior = c(0.3,0.7))
Однако, когда набор данных достаточно большой, то есть выборка примеров достаточно представительна – классификатор даст результат точнее при автоматическом определении вероятностей. Поэтому в нашем случае лучше использовать вариант записи функции без параметра prior.
> LDAmodel <- lda(formula=colour~., data=train.transformed)
Посмотрим характеристики обученного бинарного классификатора. В том числе, можем увидеть автоматически определенные вероятности распределения классов и вычисленные весовые коэффициенты линейной дискриминантной функции для каждой характеристики.
> LDAmodel
Call: lda(colour ~., data = train.transformed)
Prior probabilities of groups:
Black White
0.2496413 0.7503587
Group means:
year age sexMale employedYes citizenYes checks
Black 0.011404308 0.10786267 0.9444444 0.7097701 0.7088123 0.3010544
White -0.003794167 -0.03588548 0.9053537 0.8129382 0.8983429 -0.1001596
Coefficients of linear discriminants:
LD1
year -0.25228771
age -0.06226372
sexMale -0.40557984
employedYes 0.47180239
citizenYes 2.31968088
checks -0.52519966
Протестируем обученный классификатор на тестовых примерах.
> predictions <- predict(LDAmodel, test.transformed)$class
В качестве оценки точности классификатора можно посмотреть так называемую матрицу ошибок (confusion matrix).
> cm = as.matrix(table(predictions, test.transformed$colour))
> cm
predictions Black White
Black 45 39
White 199 761
Также посмотрим полученное качество (accuracy) обучения классификатора при работе на тестовом наборе.
> mean(predictions==test.transformed$colour)
[1] 0.7720307
Точность (precision) и полноту (recall) классификатора оценим на основе уже имеющейся матрицы ошибок, таким же способом можно рассчитать и значение уже известного качества классификатора.
> n = sum(cm)
> diag = diag(cm)
> rowsums = apply(cm, 1, sum)
> colsums = apply(cm, 2, sum)
> accuracy = sum(diag) / n
> precision = diag / colsums
> recall = diag / rowsums
> accuracy
[1] 0.7720307
> precision
Black White
0.1844262 0.9512500
> recall
Black White
0.5357143 0.7927083
Построим график линейной дискриминантной функции (рисунок 1) для каждого класса цвета кожи.
> LDAdata <- cbind(train.transformed, predict(LDAmodel)$x)
> qplot(LD1, data=LDAdata, geom="density", color=colour, fill=colour, alpha=0.5)
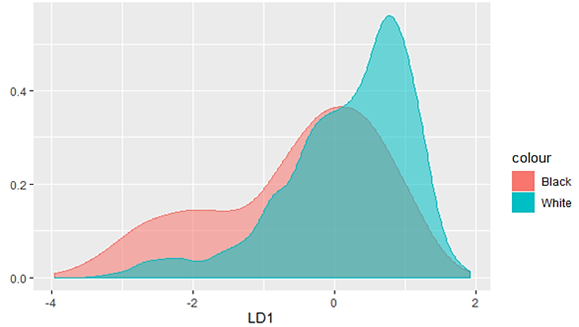
Рисунок 1 – Линейные дискриминантные функции классов
Выводы
В ходе выполнения лабораторной работы был рассмотрен метод линейного дискриминантного анализа для применения в задаче бинарной классификации, а также был разработан программный модуль бинарной классификации, и произведена оценка точности его работы.